基于KNN算法实现手写数字识别

KNN算法是分类算法中最简单的一个算法了，关于这个算法的原理我就不做详细介绍了，这么简单的算法，究竟能不能用来准确的进行分类呢？其正确率又有多高呢？

带着一点怀疑，咱来进行这个实验，我们就用最简单的KNN算法来进行手写数字识别，编程语言是python 3。

首先讲一下思路，常规的机器学习算法大致有如下几个步骤：
1、收集数据
2、数据预处理
3、寻找一个function set
4、通过对数据进行训练以找到最好的function
5、用与训练集的数据不同的测试集对这个function进行测试
6、将训练好的模型进行实际应用

但是KNN算法省去了这其中很多步骤，是不需要训练数据的，同样的也不存在找最佳的function了，因此本实验的步骤就是：
1、收集数据
2、数据预处理
3、拿测试集进行测试，并记录其正确率
4、将这个模型进行实际应用

首先导入一些需要用到的库

from numpy import *
from os import listdir
import operator
from PIL import Image

然后定义一个名为classify0的函数，该函数计算了测试数据距离数据集中每一组数据的距离，并对该距离进行排序，并运用了KNN算法返回预测结果。别看说得这么抽象，其实很简单，代码也不多，下面我会详细解释。

inX为输入的测试数据，其格式为一个1行n列的list（n为特征个数），而dataSet就算训练数据集，每一组数据占据1行，因此其为一个m×n的list（m为训练数据的数量），labels是一个m行1列的list，它对应着dataSet中每一行的标签，即预测的结果，k就算KNN算法中的那个k了。

def classify0(inX, dataSet, labels, k):
    # 获取测试数据的行数
    dataSetSize = dataSet.shape[0]
    # 请注意tile函数的作用，它将inX列表进行了复制，复制成了跟dataSetSize的行数一样的一个矩阵（不理解的请先去百度一下），然后将进行复制后的矩阵每一个值都减去dataSet，这是要为计算距离做准备了
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet
    # 差值平方
    sqDiffMat = diffMat**2
    # 计算距离，axis=1表示将每一行的值加起来，因此结果是m行1列
    sqDistances = sqDiffMat.sum(axis = 1)
    # 真正的距离，这里是开根号
    distances = sqDistances ** 0.5
    # argsort是将排序后的索引返回，注意是索引而不是数据，默认是从小到大排序
    sortedDistIndicies = distances.argsort()
    classCount = {}
    # 对排序后的数据的前k个进行操作，将该label在前k个数据中出现的次数保存在classCount这个字典中
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    # 将classCount中每个label出现的次数进行逆序排序，注意key表示的是对哪一个字段进行排序，reverse=True表示是逆序排序，即从高到低
    sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse=True)
    # 将出现次数最多的那个label返回
    return sortedClassCount[0][0]

上面是最关键的代码，下面再来进行点别的操作，首先数据自然是用现成的（我用的是Machine Learning in Action这本书中自带的），完整数据集可以在这个网站下载到：https://www.manning.com/books/machine-learning-in-action（点击左侧的resource code即可，这里采用的数据集是Ch02->digits中的数据集），文件格式如下，分为训练数据集和测试数据集

在数据集中可以看到有很多txt文件，命名为a_b.txt，其中a表示该字符是什么，而后面表示是第b个a的数据，比如0_3，表示这个txt中代表的数字是0，这是第3（或者说4）组代表数字是0的数据

每一个txt文件的内容都是由0和1组成，都是32×32，下图是一个例子

好了下面进行数据的预处理，因为函数classify0中接收的inX参数是一个1行n列的矩阵，因此我们需要一个将上图所示格式的数据转换成一个1行1024列的数据函数

# 将图片转换成vector，方便使用上面的函数
def img2vector(filename):
    returnVector = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVector[0, 32*i + j] = int(lineStr[j])
    return returnVector

下面就开始进行测试吧，代码看上去有点长，不过意思挺清楚的

def handwritingClassTest():
    hwLabels = []
    # 获取文件夹下所有文件名列表
    trainingFileList = listdir('trainingDigits')
    m = len(trainingFileList)
    trainingMat = zeros((m, 1024))
    for i in range(m):
        # 获取某一个文件名
        fileNameStr = trainingFileList[i]
        # 去掉.txt
        fileStr = fileNameStr.split('.')[0]
        # 获取第一个字符，即它是哪个数字
        classNumStr = int(fileStr.split('_')[0])
        # 保存标签
        hwLabels.append(classNumStr)
        # 数据格式化
        trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
    testFileList = listdir('testDigits')
    errorCount = 0.0
    mTest = len(testFileList)
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
        classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
        print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr))
        if classifierResult != classNumStr:
            errorCount += 1.0
    print("\nthe total number of errors is: %d " % errorCount)
    print("\nthe total error rate is: %f " % (errorCount / float(mTest)))

好了那就来执行一下吧，不得不说KNN是相当的耗资源的，运行效率不高，因为对每一组测试数据，都要计算这一组测试数据距离所有训练数据的距离，而每一组距离的计算在本例中都涉及1024次的减法+平方运算

运行结果如下，看起来还不错，准确率挺高的

既然准确率这么高，那么我何不自己写一些数字试试看呢？
于是我手写了0-9这9个数字，如下所示，然后我将用这10个数字对我的算法进行测试。

首先该做的就是数据预处理，之前的训练数据和测试数据都是txt格式的，而现在却都是自己手写的数字并拍出来的照片，因此我需要将照片转成32×32的txt文本

首先，拍出来的图片都是彩色图片，它的内部格式是3维的，而我们要让其为二维的，首先得将它转换为灰度图片。下面的函数使用了PIL中的Image工具

def transferPic2grey(originPath):
    '''
    将彩色图片转成灰度图片
    :param originPath:
    :return:
    '''
    I = Image.open(originPath)
    # 将图片大小压缩至32×32
    I = I.resize((32,32))
    # 将图片转换为灰度图片
    L = I.convert('L')
    savePath = originPath.split('.')[-2] + '_grey.jpg'
    L.save(savePath)
    return savePath

现在已经获得了32×32的灰度图片了，那么接下来就要将其变成0和1了，经过观察，我写的文字的背景色（白）的灰度图片的二进制大约为170左右，而笔迹（黑）大约为50以内，因此我又编写了一个函数用以将灰度图片转换成二进制文件。因为训练数据中笔迹用1表示，背景用0表示，因此我将二进制大于100的都置为0，小于100的都置为1

def transferGrey2binary(originPath):
    '''
    将灰度图片转换成二进制文件
    :param originPath:
    :return:
    '''
    im = Image.open(originPath)
    savePath = originPath.split('.')[-2] + "_.txt"
    fh = open(savePath, 'w')
    for i in range(im.size[1]):
        for j in range(im.size[0]):
            color = im.getpixel((j, i))
            if color > 100:
                color = 0
            else:
                color = 1
            fh.write(str(color))
        fh.write('\n')
    fh.close()
    return savePath

经过上述处理后的txt效果不错，可以用肉眼辨别出数字了，其样例图如下：

下面就定义一个测试函数，传入需要进行测试的文件的地址，该函数就会输出预测结果：

def testMyHandWriteImgRecoginze(picPath):
    picPath = transferPic2grey(picPath)
    picPath = transferGrey2binary(picPath)

    hwLabels = []
    # 获取文件夹下所有文件名列表
    trainingFileList = listdir('trainingDigits')
    m = len(trainingFileList)
    trainingMat = zeros((m, 1024))
    for i in range(m):
        # 获取某一个文件名
        fileNameStr = trainingFileList[i]
        # 去掉.txt
        fileStr = fileNameStr.split('.')[0]
        # 获取第一个字符，即它是哪个数字
        classNumStr = int(fileStr.split('_')[0])
        # 保存标签
        hwLabels.append(classNumStr)
        # 数据格式化
        trainingMat[i, :] = img2vector('trainingDigits/%s' % fileNameStr)
    vectorUnderTest = img2vector(picPath)
    classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 5)
    print("result is: %d" % int(classifierResult))

然后就跑一跑吧

for i in range(10):
    testMyHandWriteImgRecoginze(str(i)*2 + '.jpg')

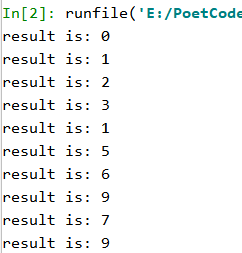
正确结果应该是0到9，可以看出实际使用的正确率比测试数据集还是低很多啦，不过总体来说还不错，正确率达到了70%，这大概是我的数据格式以及数据预处理方式和测试数据集有差别的缘故，但也比较真实了

到最后得出结论：
1、一个算法实际运用起来的正确率很大概率会比在实验室训练时所得到的正确率要低，因为你不知道输入的数据是什么格式的
2、KNN算法作为最简单的分类算法，运行效率十分低下，正确率还凑合