树

树

typedef struct TreeNode
{
    int data;
    bool isEmpty;
}TreeNode;

//初始化顺序存储的二叉树，所有结点标记为"空"
void InitSqBiTree (TreeNode t[], int length) {
    for (int i=0; i<length; i++){
        t[i].isEmpty=true;
    }
}

int main(){
    TreeNode t[100];        //定义一棵顺序存储的二叉树
    InitSqBiTree(t, 100);   //初始化为空树
    //...
}

实现函数，找到结点 i 的父结点、左孩子、右孩子

若顺序二叉树从数组下标1开始存储结点，则：

• 结点 i 的父结点编号为 i/2
• 结点 i 的左孩子编号为 i*2
• 结点 i 的右孩子编号为 i*2+1

！！！！重要！！！！

若顺序二叉树从数组下标0开始存储结点，则：

• 结点 i 的父结点编号为 [(i+1)/2] - 1 = (i -1)/2
• 结点 i 的左孩子编号为 [(i+1)2] - 1 = 2i + 1
• 结点 i 的右孩子编号为 [(i+1)2+1] - 1 = 2i + 2

//判断下标为 index 的结点是否为空
bool isEmpty(TreeNode t[], int length, int index){
    if (index >= length || index < 1) return true;   //下标超出合法范围
    return t[index].isEmpty;
}

//找到下标为 index 的结点的左孩子，并返回左孩子的下标，如果没有左孩子，则返回 -1
int getLchild(TreeNode t[], int length, int index){
    int lChild = index * 2;   //如果左孩子存在，则左孩子的下标一定是 index * 2
    if (isEmpty(t, length, lChild)) return -1;  //左孩子为空
    return lChild;
}

//找到下标为 index 的结点的右孩子，并返回右孩子的下标，如果没有右孩子，则返回 -1
int getRchild(TreeNode t[], int length, int index){
    int rChild = index * 2 + 1;                 //如果右孩子存在，则右孩子的下标一定是 index * 2 + 1
    if (isEmpty(t, length, rChild)) return -1;  //右孩子为空
    return rChild;
}

//找到下标为 index 的结点的父节点，并返回父节点的下标，如果没有父节点，则返回 -1
int getFather(TreeNode t[], int length, int index){
    if (index == 1) return -1;          //根节点没有父节点
    int father = index / 2;             //如果父节点存在，则父节点的下标一定是 index/2，整数除法会自动向下取整
    if (isEmpty(t, length, father)) return -1;
    return father;
}

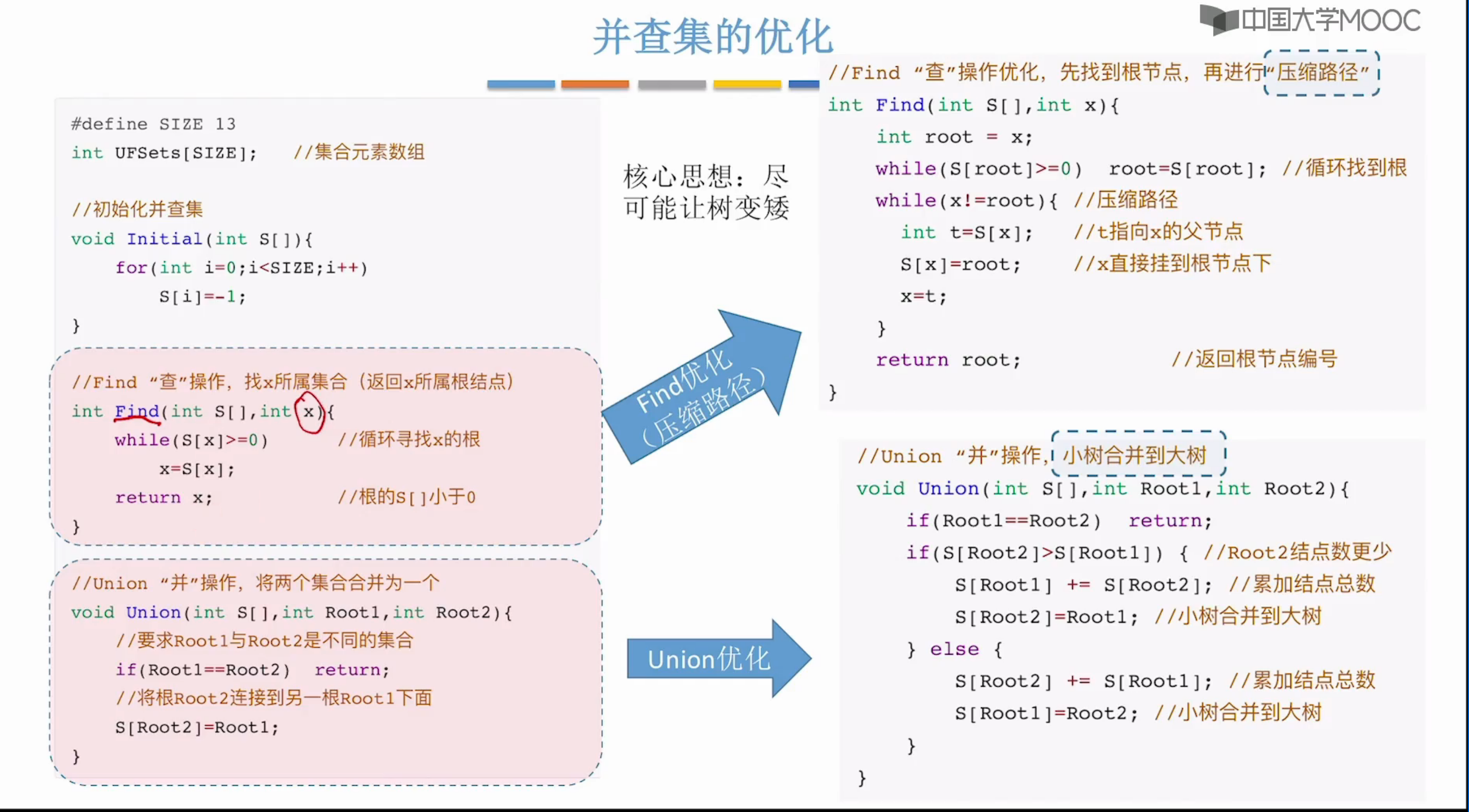
并查集

双亲表示法，实现并查很方便

#define SIZE 100
int UFSets[SIZE];

//初始化
void initial(int s[]){
    for (int i = 0; i < SIZE; i++)
    {
        s[i] = -1;
    }
}

//并	o(1)
void Union(int s[], int root1, int root2){
  if (root1 == root2)   return;
  s[root2] = root1;   //把root2连到root1下面
}

//并优化
void Union2(int s[], int root1, int root2){
    if (s[root2]>s[root1])
    {   
        s[root1] += s[root2];
        s[root2] = root1;
    }else{
        s[root2] += s[root1];
        s[root1] = root2;
    }   
}

//查 o(n)
int Find(int s[], int x){
    while (s[x]>=0)
    {
        x = s[x];      //循环找x根
    }
    return x;   //返回根
}

并查集的应用

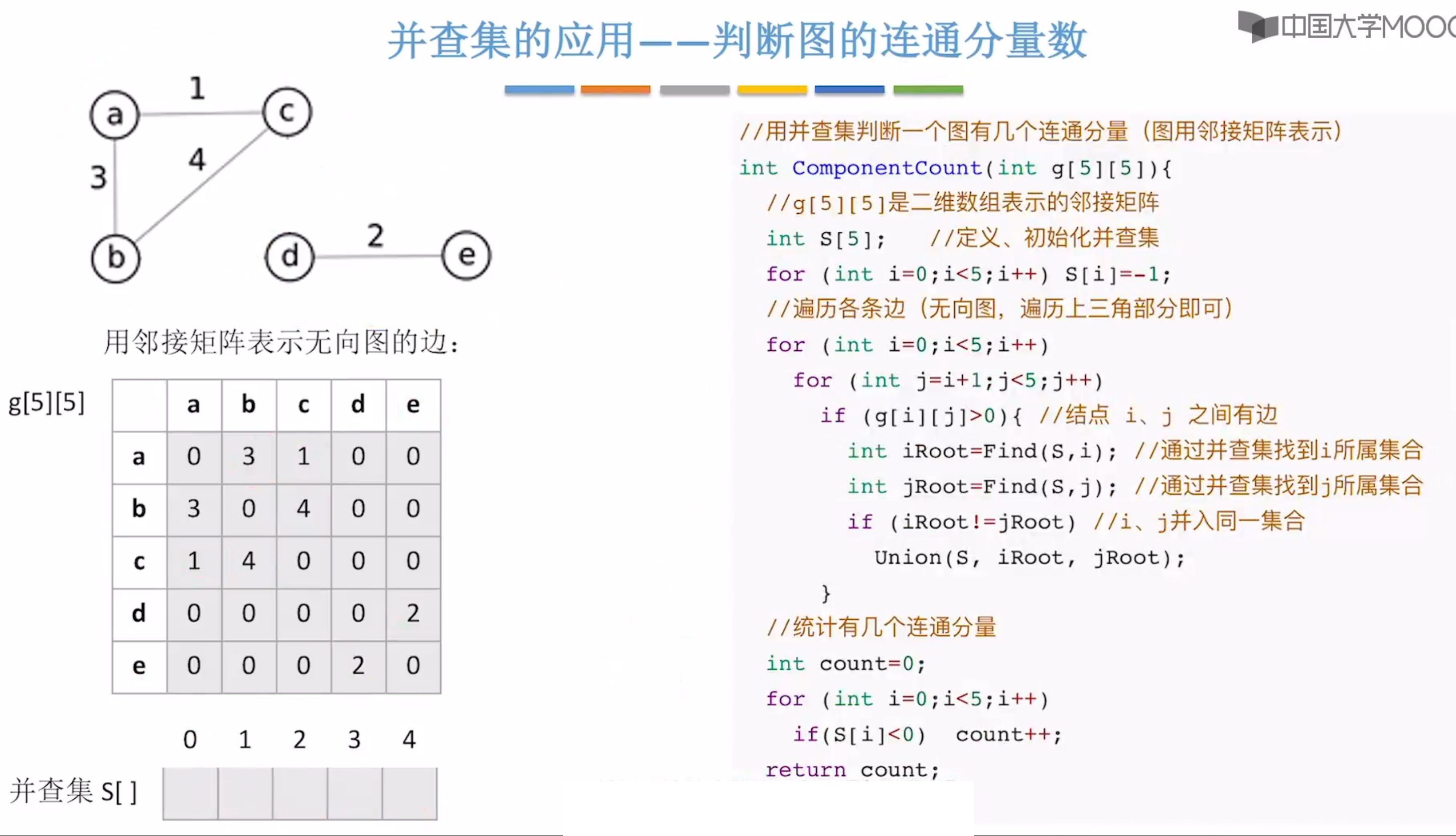
如果连通分量的数量 == 1 则图是连通的，大于1则不丝滑连通图。

判断是否有环：

并查集优化