Factorization Machine 因子分解机
1 FM模型
FM是一般线性模型的推广,一般的线性模型可以表示为(式0):
\[y(x)=w_0+\sum_\limits{i=1}^{n}{w_i}x_i
\]
但是上述模型没有考虑特征间的关联,为表示关联特征对\(y\)的影响,引入多项式模型,以\(x_iy_i\)表示两特征的组合,有如下二阶多项式模型(式1):
\[y(x)=w_0+\sum_\limits{i=1}^{n}{w_ix_i}+\sum_\limits{i=1}^{n-1}{\sum_\limits{j=i+1}^{n}{w_{ij}x_ix_j}}
\]
其中,\(x_i\)表示第\(i\)个特征,n表示特征的个数。
由式1可知,组合特征及其参数的的个数为\(\frac{n(n-1)}{2}\)个,若特征数据很密集,则可以使用传统方法求解。但若在CTR预估等场景中,进行One-Hot Encoding后,特征会变得非常稀疏(Sparse),满足\(x_ix_j\)都不为零的记录很少,使用传统方法求解会带来很大的误差。
FM很好的解决了这个问题,观察,由\(w_{ij}\)组成的矩阵可以表示为
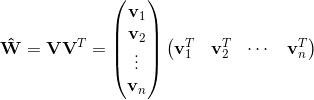
即对应的\(w_{ij}=v_iv_j^T\),可以将\(v_i\)和\(v_j\)看作是\(x_i\)和\(x_j\)自带的辅助向量(这俩向量就是求解的目标),具体地\(v_i=(v_{i1},v_{i2},...,v_{ik})\),\(v_i\)的维度\(k\)反映了模型的表达能力。因此,二阶多项式模型也可以表示为(式2):
\[y(x)=w_0 + \sum_\limits{i=1}^{n}{w_ix_i} + \sum_\limits{i=1}^{n}{\sum_\limits{j=i+1}^{n}{\langle v_i,v_j\rangle x_ix_j}}
\]
将组合特征的参数\(w_{ij}\)转化为\(\langle v_i,v_j\rangle\),确保了在稀疏的情况下仍然能够求得\(w_{ij}\)的解,这就是FM的核心思想。
### 2 FM的求解



