numpy的介绍——总览
为什么有numpy这个库呢?
1. 准安装的Python中用列表(list)保存一组值,可以用来当作数组使用,不过由于列表的元素可以是任何对象,因此列表中所保存的是对象的指针。这样为了保存一个简单的[1,2,3],需要有3个指针和三个整数对象。对于数值运算来说这种结构显然比较浪费内存和CPU计算时间。
2. 此外Python还提供了一个array模块,array对象和列表不同,它直接保存数值,和C语言的一维数组比较类似。但是由于它不支持多维,也没有各种运算函数,因此也不适合做数值运算。
3. 所以numpy就这么登场了,NumPy是Python的一种开源的数值计算扩展。这种工具可用来存储和处理大型矩阵,比Python自身的嵌套列表(nested list structure)结构要高效的多(该结构也可以用来表示矩阵(matrix))。 NumPy的主要对象是同种元素的多维数组。这是一个所有的元素都是一种类型、通过一个正整数元组索引的元素表格(通常是元素是数字)。在NumPy中维度(dimensions)叫做轴(axes),轴的个数叫做秩(rank)。
4. numpy的所有的函数docs 可以看:https://docs.scipy.org/doc/numpy/genindex.html
numpy 提供了两个基本的对象: ndarray 和 ufunc. ndarray是存储数据的多维数组, 而 ufunc 是对数组进行处理的函数。
以下内容参考自:python科学计算 第二章的内容。
ndarray对象:
1. 如何创建一个ndarray对象——数组??
方法一: 使用 np.array()函数把 python传入的序列对象创建成数组。 这个序列对象可以是用 []括起来的列表,也可以是用()括起来的元组。 多层序列嵌套使用 , 隔开。例子如下:
#使用列表作为参数: >>> np.array([1, 2, 3]) array([1, 2, 3]) >>> np.array([[1, 2],[3, 4]]) array([[1, 2], [3, 4]]) #使用带括号的元组作为参数 >>> np.array((4, 5, 6)) array([4, 5, 6]) >>> np.array(((4, 5),(5, 6))) array([[4, 5], [5, 6]])方法二:
np.arange()函数可以通过指定开始值、终值、步长来创建一个等差数列, 不包括终值;
np.linspace()函数可以通过指定开始值、终值、元素个数创建等差数列, 通过endpoint参数指定是否包括终值,默认包括;
np.logspace() 函数创建等比数列,具体用法使用help()查看。
zeros()、ones()和empty()函数可以创建指定的数组, 参数使用元组或列表, 大家一般都使用元组,例如:
>>> np.ones((2,2)) array([[ 1., 1.], [ 1., 1.]]) >>> np.zeros((2,2)) array([[ 0., 0.], [ 0., 0.]]) >>> np.empty((2,2)) array([[ 1.25849429e-316, 4.71627160e-317], [ 6.91798776e-310, 0.00000000e+000]])zeros_like() 、 ones_like()和empty_like()创建与参数的数组相同形状的数组;
frombuffer()、 fromstring()、 fromfile()等函数可以从字节序列或文件创建数组
使用: fromfunction()通过此函数创建数组, func的参数就是数组元素的索引。例如:
>>> def func(i): ... return i * i ... >>> np.fromfunction(func, (9,)) array([ 0., 1., 4., 9., 16., 25., 36., 49., 64.])
充小知识点:
1) 使用数组的 shape 属性可以查看一个数组的形状,它的返回值是一个元组:
>>> a = np.array([[1, 2], [3, 4]]) >>> a array([[1, 2], [3, 4]]) >>> a.shape (2, 2)2)可以通过修改 shape的属性来修改一个数组的元素, 但是它内存位置不变化 。 例如:
3) 还可以通过 reshape()方法,修改原数组的形状来创建一个新数组, 特征注意: 新建的数组与原数组是共享内存空间的, 修改其中一个就会影响另一个!!!>>> a.shape = (4, 1) >>> a array([[1], [2], [3], [4]]) >>> a.shape = (4,) >>> a array([1, 2, 3, 4])>>> b = a.reshape((2,2)) >>> b array([[1, 2], [3, 4]])4) 当使用reshape()方法时, 如果其它一个轴的大小设置 为 –1, 则自动计算该轴的长度;
5) 数组元素的类型可以通过 dtype 获得, 各个类型都存储在 np.typeDict 字典里。
2. 读取数组:
使用 [] 操作符对数组内的元素进行读取 , 那么下标都可以是什么呢?
1. 使用整数, 整数的下标是从0开始的; 如 a[0]等;
2. 使用切片, 切片的使用这里不多说明。只说明一点为: 切片得到的数组与原始数组共享内存单元。
3. 使用整数列表, 如:[1, 3, 5], 说明:使用它得到的新数组与原始的数组不共享内存单元。
4. 使用整数数组, 可以是多维的, 它同样不会共享内存单元。 如:
>>> b array([[1, 2, 3], [4, 5, 6]]) >>> a = np.arange(100,120,2) >>> a array([100, 102, 104, 106, 108, 110, 112, 114, 116, 118]) >>> a[b] array([[102, 104, 106], [108, 110, 112]])
5. 使用布尔数组, 这个很有意思!!!, 它只保留是对应是 true 的元素。 布尔数组一般都是生成的,例如:
>>> x = np.random.rand(8) >>> x array([ 0.3179888 , 0.44513988, 0.94475611, 0.8954217 , 0.79704721, 0.33844282, 0.56761519, 0.87936442]) >>> x > 0.5 array([False, False, True, True, True, False, True, True], dtype=bool) >>> x[x>0.5] array([ 0.94475611, 0.8954217 , 0.79704721, 0.56761519, 0.87936442])
3. 多维数组:
1. 在多维数组中,使用元组作为数组的下标, 元组的每一个元素与数组的每一个轴对应, 当元组中的元素个数少于少于数组的维数时,默认剩余的各轴为 :, 即表示所有。 a[1, 2] 与a[(1, 2)] 是一样的;
2. 下标对象不是元组, NumPy 会首先把它转换为元组。这种转换可能会和用户所希望的不一致,因此为了避免出现问题,请显式地使用元组作为下标。
3. 元组中的每一个元素可以是一个整数, 也可以是一个列表,也可以又是一个元组,也可以是一个数组,也可以是一个布尔数组。 在最后, 这些经过各种转换和添加“:”之后 ,
得到了一个标准的下标元组。它的各个元素有如下几种类型:切片、整数、整数数组和布尔数组。如果元素不是这些类型,如列表或元组,就将其转换成整数数组!!!!
4. 如果下标元组的所有元素都是切片,那么用它作为下标得到的是原始数组的一个视图,即它和原始数组共享数据存储空间。 可以使用 a.flags查看一下 OWNDATA字段,如果为False,则是共享的。
当在下标中使用这些对象时,所获得的数据是原始数据的副本,因此修改结果数组不会改变原始数。
>>> a array([[10, 11, 12, 13, 14], [20, 21, 22, 23, 24], [30, 31, 32, 33, 34], [40, 41, 42, 43, 44]]) #使用列表作为元组的第一个元系,第二个元素省略; >>> a[[1,2]] array([[20, 21, 22, 23, 24], [30, 31, 32, 33, 34]]) # 使用两个元组, 它值其实就是a[0,2]和a[1, 3] >>> a[(0,1), (2,3)] array([12, 23]) #使用一个二维数组作为元组中的第一个元素, 第十个元素省略, 这样会得到一个三维的数组; >>> a array([[10, 11, 12, 13, 14], [20, 21, 22, 23, 24], [30, 31, 32, 33, 34], [40, 41, 42, 43, 44]]) >>> b array([[1, 2], [3, 1]]) >>> b.shape (2, 2) >>> a[b] array([[[20, 21, 22, 23, 24], [30, 31, 32, 33, 34]], [[40, 41, 42, 43, 44], [20, 21, 22, 23, 24]]]) >>> a[b].shape (2, 2, 5)
4. 结构数组:
可以自行创建一个结构数组的类型. 然后,就可以使用这个结构类型创建结构数组了. 只举一个简单的例子:
# 创建一个结构体类型, 是一个字典类型,里面有names与formats的键, 键值为一个列表 persontype = np.dtype({ 'names':['name', 'age', 'weight'], 'formats':['S32','i', 'f']}, align= True ) #使用结构类型创建结构数组 a = np.array([("Zhang",32,75.5),("Wang",24,65.2)], dtype=persontype)
其中:
'S32' :长度为 32 字节的字符串类型,由于结构中每个元素的大小必须固定,因此需要指定字符串的长度。
'i' : 32 bit 的整数类型,相当于 np.int32。
'f' : 32 bit 的单精度浮点数类型,相当于 np.float32。
5 内存结构
这一部分讲明了为什么切片操作,可以是共享原始数据的内存,而不用复制的。
每一个数组都可以使用flags属性查看相关的信息,如:
>>> a array([[10, 11, 12, 13, 14], [20, 21, 22, 23, 24], [30, 31, 32, 33, 34], [40, 41, 42, 43, 44]]) >>> a.flags C_CONTIGUOUS : True F_CONTIGUOUS : False OWNDATA : True WRITEABLE : True ALIGNED : True UPDATEIFCOPY : False
ufunc运算
ufunc 是 universal function 的缩写,它是一种能对数组中每个元素进行操作的函数。 NumPy内置的许多 ufunc 函数都是在 C 语言级别实现的,因此它们的计算速度非常快。
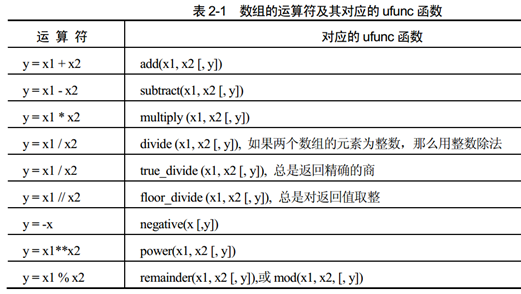
1. 四则运算
它提供了数组的四则运算的相关函数, 即可以通过函数调用进行四则运算,也可以直接使用 运算符进行计算。
其中, 除号的意义根据是否激活 __future__.division 会有所不同:python 2 与 python3中的除法问题。
2.2 比较和布尔运算
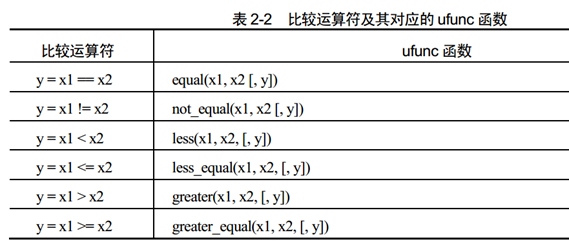
1. 比较操作:
使用”==“、”>”等比较运算符对两个数组进行比较, 将返回一个布尔数组, 它的每一个元素值都是两个数组对应元素比较的结果。
2. 布尔运算:
由于 Python 中的布尔运算使用 and、 or 和 not 等关键字,它们无法被重载,因此数组的布 尔运算只能通过相应的 ufunc 函数进行。这些函数名都以“logical_”开头, 包括:
np.logical_and()、 np.logical_not()、 np.logical_or() 、 np.logical_xor()四个函数。 使用方法例如:
>>> a>b array([False, False, True, True], dtype=bool) >>> a<b array([ True, True, False, False], dtype=bool) >>> np.logical_or(a>b, a<b) array([ True, True, True, True], dtype=bool)
注意: 当我们对布尔数组使用 python的逻辑运算符 and ,or, not 操作时,会提示错误,原因在于,它们只能比较单个的布尔值,不能比较多个。
>>> a>b or a<b Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
3. 比特运算函数:
以“bitwise_”开头的函数是比特运算函数,包括 bitwise_and、 bitwise_not、 bitwise_or 和 bitwise_xor 等。也可以使用"&"、 "~"、 "|"和"^"等操作符进行计算。 对于布尔数组来说,位运算和布尔运算的结果相同。
4. 广播
什么意思呢?当两个数组的维度不对应是,如何进行四则运算呢???这时候,数组就会被扩展处理(广播处理):
原则(抄书上写的):
(1) 让所有输入数组都向其中维数最多的数组看齐, shape 属性中不足的部分都通过在前面加 1 补齐。
(2) 输出数组的 shape 属性是输入数组的 shape 属性在各个轴上的最大值。
(3) 如果输入数组的某个轴长度为 1 或与输出数组对应轴的长度相同,这个数组就能够用来计算,否则出错。 (意思就是说为1时,可以进行扩展了)
(4) 当输入数组的某个轴长度为 1 时,沿着此轴运算时都用此轴上的第一组值。
举例说明:
#创建一个二维数组 a,其形状为(6,1): >>> a = np.arange(0, 60, 10).reshape(-1, 1) >>> a array([[ 0], [10], [20], [30], [40], [50]]) >>> a.shape (6, 1) #再创建一维数组 b,其形状为(5,): >>> b = np.arange(0, 5) >>> b array([0, 1, 2, 3, 4]) >>> b.shape (5,) #计算数组 a 和 b 的和,得到一个加法表,它相当于计算两个数组中所有元素组的和,得到一个形状为(6,5)的数组 >>> c = a + b >>> c array([[ 0, 1, 2, 3, 4], [10, 11, 12, 13, 14], [20, 21, 22, 23, 24], [30, 31, 32, 33, 34], [40, 41, 42, 43, 44], [50, 51, 52, 53, 54]]) >>> c.shape (6, 5) #惊讶了吗??,下面解释一下: #由于数组 a 和 b 的维数不同,根据规则(1),需要让数组 b 的 shape 属性向数组 a 对齐,于是将数组 b 的 shape 属性前面加 1,补齐为(1,5)。相当于做了如下计算 >>> b.shape=1,5 >>> b array([[0, 1, 2, 3, 4]]) #根据规则(2),输出数组各个轴的长度为输入数组各个轴长度的最大值,可知输出数组的 shape 属性为(6,5)。 #由于数组 b 第 0 轴的长度为 1,而数组 a 第 0 轴的长度为 6,因此为了让它们在第 0 轴上能够相加,根据(4)需要将数组 b 第 0 轴的长度扩展为 6,这相当于: >>> b = b.repeat(6,axis=0) >>> b array([[0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4]]) # 数组a 同理,作相同的操作: >>> a = a.repeat(5, axis=1) >>> a array([[ 0, 0, 0, 0, 0], [10, 10, 10, 10, 10], [20, 20, 20, 20, 20], [30, 30, 30, 30, 30], [40, 40, 40, 40, 40], [50, 50, 50, 50, 50]]) #经过上述处理之后,数组 a 和 b 就可以按对应元素进行相加运算了。
另外, np.ogrid提供了可以快速产生能够进行广播运算的数组。 np.mgrid对象与ogrid类似,它的返回值是进行广播扩展之后的数组。其切片下标有两种形式:
● 开始值:结束值:步长,和“np.arange(开始值, 结束值, 步长)”类似。
● 开始值:结束值:长度 j,当第三个参数为虚数时,它表示所返回数组的长度,其和“np.linspace(开始值, 结束值, 长度)”类似
例如:
>> x, y = np.ogrid[:4, :4] >>> x array([[0], [1], [2], [3]]) >>> y array([[0, 1, 2, 3]]) >>> x, y = np.mgrid[:4, :4] >>> x array([[0, 0, 0, 0], [1, 1, 1, 1], [2, 2, 2, 2], [3, 3, 3, 3]]) >>> y array([[0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3]])
(以上内容写于:2017年11月3日)