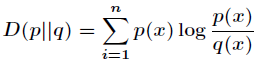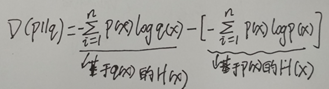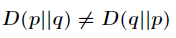关于信息论中熵的定义与含义:
信息熵:
1. 热力学中的热熵是表示分子状态混乱程度的物理量。香农用信息熵的概念来描述信源的不确定度。
2. ;两个独立符号所产生的不确定性应等于各自不确定性之和
3. 在信源中,考虑的不是某一单个符号发生的不确定性,而是要考虑这个信源所有可能发生情况的平均不确定性。
对于当个符号,它的概率为p时,用这个公式衡量它的不确定性:
而信源的平均不确定性,称为信息熵,用下面的公式表示:
注意:1. 当式中的对数的底为2时,信息熵的单位为比特。它底数为其它时,它对应的单位也不一样。
2. 信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。所以,信息熵也可以说是系统有序化程度的一个度量。
条件熵:
设X,Y是两个离散型随机变量,随机变量X给定的条件下随机变量Y的条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。 公式推导如下:
注意:
注意:1. 这个条件熵,不是指在给定某个数(某个变量为某个值)的情况下,另一个变量的熵是多少,而是期望! 因为条件熵中X也是一个变量,意思是在一个变量X的条件下(变量X的每个值都会取),另一个变量Y熵对X的期望。
2. 在计算信息增益的时候,经常需要用到条件熵。信息增益(information gain)是指期望信息或者信息熵的有效减少量(通常用“字节”衡量)。通常表示为:信息熵 - 条件熵;在决策树中就是根据信息增益选择特征的;
相对熵 或 K-L散度
设p(x)和q(x)是 X 取值的两个概率分布,则 p 对于 q 的相对熵为:
它其实吧,有点意思的, 卡式可以写成这样子:
KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q 表示数据的理论分布,模型分布,或P的近似分布。
注意:1. KL散度不是对称的,即:
2. 相对熵的值为非负值。 可以从一个很重要的不等式中推论出来,即吉布斯不等式:
以上内容参考:http://blog.csdn.net/acdreamers/article/details/44657745
交叉熵:
它的公式如下:
它的本质含义为:编码方案不一定完美时,平均编码的长度是多少。
通过公式很好理解。。。。 再结合相对熵更容易明白什么含义了。
另外, 我自己补充一点:
在人工神经网络中,我们有时候会作用交叉熵作为代价函数,此时吧,我们实际上是把输出看作为一个贝努力分布的的。论文 Extracting and composing robust features with denoising autoencoders里有说明。
上面三者的区别:
下面是一个总结,我在知乎上看到的,我的理解也是这个意思,这里引用过来:
1)信息熵:编码方案完美时,最短平均编码长度的是多少。
2)交叉熵:编码方案不一定完美时(由于对概率分布的估计不一定正确),平均编码长度的是多少。
平均编码长度 = 最短平均编码长度 + 一个增量
3)相对熵:编码方案不一定完美时,平均编码长度相对于最小值的增加值。(即上面那个增量)作者:张一山
链接:https://www.zhihu.com/question/41252833/answer/140950659
来源:知乎
互信息:
先说点其它的:有两个变量,分别为X与Y, 则X的信息熵为H(X), Y的信息熵为H(Y), 然后呢,
问: x与y的联合分布的信息熵,就可以表示为H(X,Y) 。如果 X与Y独立的话,则有 H(X,Y) = H(X) + H(Y)。如果不独立的话,则有:H(X,Y) = H(X) + H(Y|X) = H(Y) + H(X|Y)。
现在呢,互信息就可以表示为:
I(X,Y) = H(X) + H(Y) – H(X,Y)
这个公式,对应的含义就是:它可以看成是一个随机变量中包含的关于另一个随机变量的信息量。
另外,我们还可以把互信息写为: I(X,Y) = H(X) – H(X|Y) = H(Y) – H(Y|X)
此时,互信息可以说成一个随机变量由于已知另一个随机变量而减少的不肯定性。
是不是有点意思??很好理解吧。