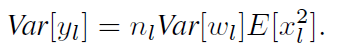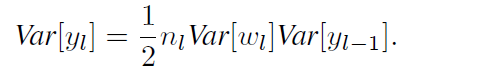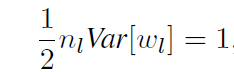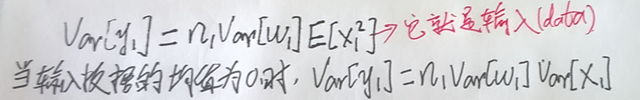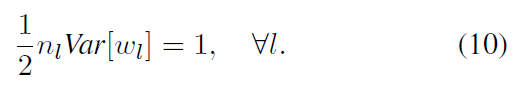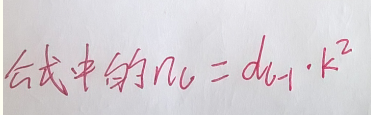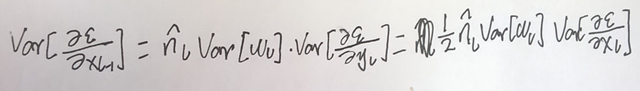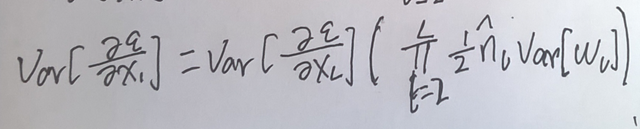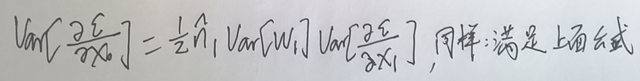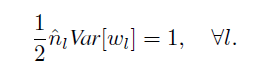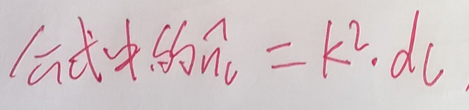微软亚洲实验室一篇超过人类识别率的论文：Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification ImageNet Classification

在该文章的两大创新点：一个是PReLU,一个是权值初始化的方法。下面我们分别一一来看。

PReLU(paramter ReLU)

所谓的PRelu，即在 ReLU激活函数的基础上加入了一个参数，看一个图就明白了：

右边的图上多了一个参数吧，在负半轴上不再为0，而是一个可以学习的斜率。很容易明白。实验结果显示该方法可以提高识别率。

权值初始化的方法：

对于文中的权值初始化问题：主要思想是跟随了“Xavier”的初始化的思想，研究了第一层layer的响应的 variance。下面的推导过程是基于ReLU激活函数的。分为一下两种情况来分析：

forward propagation：

在推导前，先说一些符号的代表意义：y_L表示第L层上的一个feature map上的一个神经单元的response（这里的response指的是上一层的所有连接单元的加权和，是不经过激活函数哈，这里把激活函数作另外的一个行为吧）；yL 经过激活函数看得到的值我们记作XL；b_L表示偏置；L层的feature map的个数用 d_L表示; 卷积核的大小表示为k*K（可能不同的layer的卷积核不一样哦，这里就不区分了）; 激活函数表示为f()；

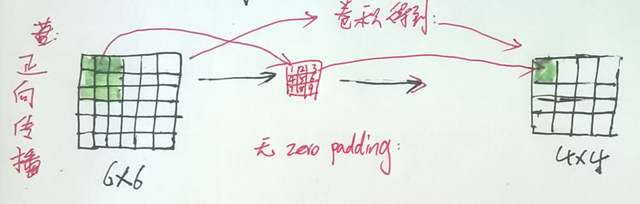
以下为正向传播的卷积过程（只画出了一个feature map的情况）：

其中一个输出值用公式表示如下（接收域的feature map 的个数为 d_L-1) ：

接下来呢，我们会这么做：

1. 初始化时，我们把权值WL里的各元素初始化为独立同分布的变量，且令 WL 的均值为 0 ；

2. 我们假设元素 XL 的变量也是独立同分布的变量；

3. WL 与 XL 是相互独立的；

往下的推导会用于以下概率论中的知识：

对于随机变量X，它的期望可以表示为EX，下面看看它的方差怎么表示：
DX ＝ E（X－EX）²＝ E（X²－2XEX +（EX）²）＝ EX² －（EX）²
所以当 EX＝0时，DX ＝ EX²
当随机变量X与随机变量Y相互独立时，我们有这样的结论：
EXY ＝ EX * EY
DXY = EX²EY² –(EX)²(EY)²
D(X+Y) = DX + DY

在上面的条件下我们继续推导，推导的核心为求 response 的方差（variance)：

所以就得到了：

然后呢，我们让W _L_-1的对称分布在0值的左右，这样同时也就可以让 W 的均值为0 （或期望为0）了，然后，这样的话， y_L-1 的分布也是对称分布在0值左右了。y_L-1的期望也为0 了。所以就有了下面的结果：

代入到上面公式中得到：

把L层的layer 联合起来，我们可以得：

为了使 y1 的方差与 yL 的方差相等，我们就需要另：

，其中 l = 2, 3, 4, …… L。

对于第一层的输入，我们有这样的公式：

所以第一层对应的条件为:

为了各层之间统一起来, 第一层差个1/2也没事,所以呢,对于前向传导,权值应该满足这样的条件:

其中:

，K 为第K层的卷积核的大小。

结论: 权值满足 mean 为0, 方差为 2/ nl 的条件.

Backward Propagation :

对于反向传播时，利用BP算法，当我们在推导公式中，总要求出目标函数对每一层的输入值的偏导数。下面的公式如果你没有推导过这个BP过程的话，可能有点看不懂哦：

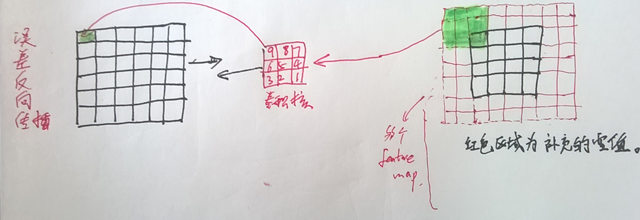
上面的公式可能和论文里的有点不一样，因为吧，论文里一次性把多个feature map上的对应元素求出来了，我觉得对于下面的推导，求一个就够了。对于上面公式的过程，我自己画了一个图表示一下：

对上图的说明：1，我只画出了一个 feature map的情况；2，还有注意卷积核，与正向传播时的卷积核有差别（旋转了180度）；3，卷积的对象以及输出的对象都是偏导数；4,可以与正向传播时作个对比；

下面为推导过程，也是围绕着方差来的：

然后，就得到了：

当我们把L层合在一起时，变为了：

当然，对于X0（它表示网络的输入）没有必要去求偏导数，但是为了推出第一层网络权值满足的条件，我们也可以写出来：

，它同样符合公式的哦，我已经证明过了。。。

对于前向传导时，在第一层会有一个1/2的差别，但是在这反向传播中没有。其实反射传播也存在一层的差别，只不过是在L+1层，因为在第L层往后可能没有激活函数了。

所以呢，在反向传播过程中，为了使偏对数的方差相同的话，那么需要满足的条件为：

，K 为第L层的卷积核。