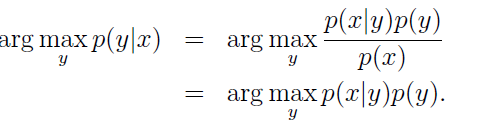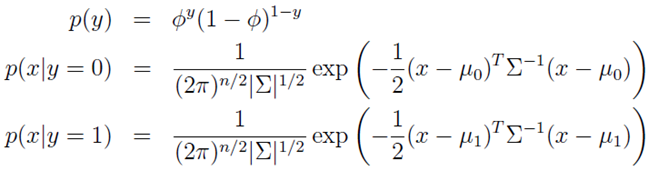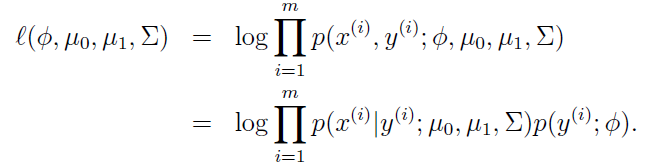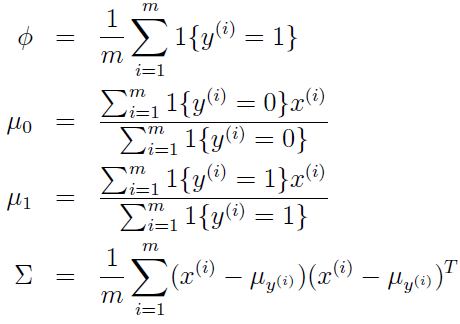高斯判别分析模型
对于常见的分类算法,经常用到的都是判别学习算法,如 logistic二元分类器,还有softmax分类器等。它们都有一个共同的特点,那就是我们直接去求 p(y|x; θ), 有时候也表示为 hθ(x),这类方法的重点是去拟合参数θ。
还有一种算法:生成学习算法。它的中心思想是直接去求p(y|x; θ)很难,然后转而去求 p(x|y) 与p(y ), 然后利用贝叶斯公式得到:p(y|x) = p(x|y) * p(y )/ p(x)。
下面介绍生成学习算法中的高斯判别分析:
它是核心假设为:p(x|y)服从高斯分布。这个假设的含义就是指在给定某一类别下,所属类别的所有样本的分布为高斯分布。这个假设在大多数情况下是成立的。
下面以两分类(伯努利分布)来说明一个高斯判别分析:
当我们求p(y|x)时, 我们利用叶斯公式:
对于分类问题,我们不用关心p(x),因为我们求的是所属类 Y 的概率大小啊,所以我们只关心分子就可以啦,即:
如果我们非得想求出p(x)也可以,利用全概率公式就可以求出来了,即 p(x) = p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0)。
下面呢,让我们看一下各自的分布情况哈:
由于 y服从伯努利分布,而p(x|y)服从的为高斯分布,所以呢,可以写作:
注意:虽然类别分别为0与1,但是我们用了相同的协方差矩阵。当然也可以用不相同的协方差矩阵。
然后呢,对于一个训练样本集合来说,我们可以写出它的拟然函数来,如下所示为log形式的拟然函数:
为使似然函数得到最大值,对参数求使层数为 0,我们得到对应的参数的值:
到现在为止,我们就得到了高斯判别分析模型了,它可以用于分类的哦,分类时,我们的核心假设为对于每类中的样本分布呈现高斯分布。
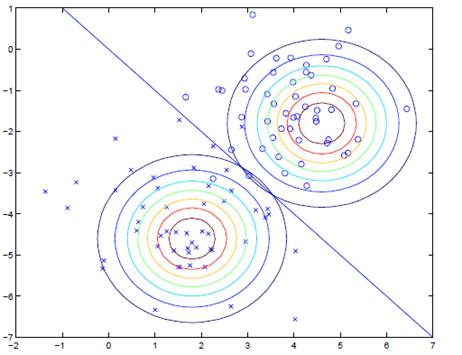
我们来看一个直观的的例子,下图为二维的情况下的图哈,变量x 为二维的。
高斯判别分析模型与logistic模型的关系:
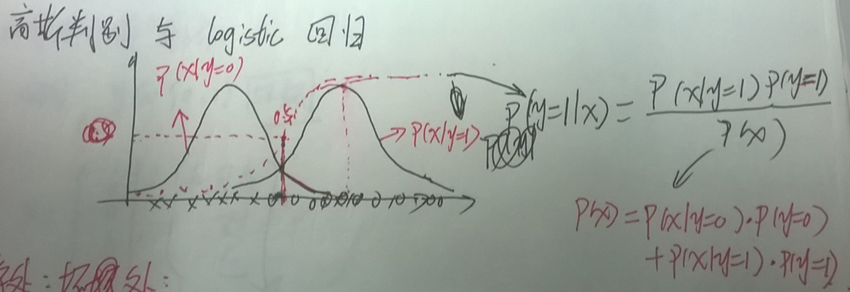
在两分类上,我们也可以用logistic模型进行分类(它属于判别学习算法),我们看看高斯判别模型与logistic回归模型的关系哈,先看个图:
说明了什么呢?
其实 上图中的losgtic回归网线就是p(y=1|x) = p(x |y=1)p(y=1) / p(x)的曲线。 两个高斯分布交界的地方就是logistic曲线等于0.5的地方, 因为在这一点 p(y = 0) 与 p(y =1)的概率相同。
当p(x |y )服从高斯分布时,我们可以推出logistic回归,但是呢反推是不成立的。 所以呢, 当p(x |y)真的服从高斯分布时,我们用高斯判别分析比logistic模型更好。
总之呢,高斯判别作出了更强的假设,需要少的数据,并且大大部分的情况下结果很好的,而logistic回归模型通常更加泛化。
参考:ufldl 教程;