Logistic 分类器与 softmax分类器
首先说明啊:logistic分类器是以Bernoulli(伯努利) 分布为模型建模的,它可以用来分两种类别;而softmax分类器以多项式分布(Multinomial Distribution)为模型建模的,它可以分多种互斥的类别。
补充:
什么是伯努利分布?伯努利分布[2] 是一种离散分布,有两种可能的结果。1表示成功,出现的概率为p(其中0<p<1)。0表示失败,出现的概率为q=1-p。
什么是二项分布?二项分布即重复多次的伯努利分布哦;
什么是多项式分布?即它把两种状态推广到了多种状态,是二项分布的推广;
Logistic 分类器
要解决什么样的问题呢??假设有一训练样本集合X = {x1, x2, x3, ……},其中样本 xi 由一系列的属性表示即,xi = (a1, a2, a3,……),并且对于样本集合X中的样本要么属于类别0, 要么属于类别1.
现在呢,我们有一个测试样本x, 我们根椐上面的知识来推断: 样本x 属于类别0 还是类别1呢??
下面来解决这个问题哦:
1,首先引入参数θ=(θ1,θ2,θ3,……),对于样本中的属性进行加权,得到:θTx
2,引入logistic函数(sigmoid函数):g(z) = 1 / (1 + e-z), 该函数常作为神经网络里的激活函数的;构建这么一个式子(待会就会明白它的含义):
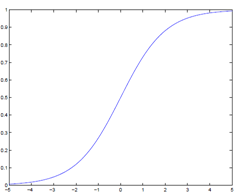
logistic函数的图像为:
我们发现呢,它总是介于0-1之间呢,所以呢,我们可以让 hθ(x) 函数作为一种概率估计哦,如,我们可以让它表示样本 x 属于类别1的概率,即 P(y = 1 | x; θ) = hθ(x) 。 其实一开始可能不那么容易理解,不过你这么想想,给定了样本 x , 当θTx的值大于0时,则hθ(x)大于0.5,表示样本为类别1的概率超过了50%,而如果当θTx的值小于0时,则hθ(x)大、小于0.5,表示样本为类别1的概率不会超过50%,那么它属于类别0的概率超过了50%了啊,所以呢,hθ(x) 函数作为样本 x 属于哪种类别的概率估计很好啊,关键问题就是根椐训练样本求出合适的参数θ。
3. 现在我们有: P(y = 1 | x; θ) = hθ(x) , 与 P(y = 0 | x; θ) = 1 - hθ(x), 那么呢,我们把它俩联合起来, 得到:P(y | x; θ) = {hθ(x)}y{(1-hθ(x)}1-y.
4. 现在,我们有了 P(y | x; θ) ,它的含义就是在给定样本 x 与参数 θ 时,标签为y 的概率; 然后我们还有一个训练样本集合(已经每个样本的标签)。现在我们假设每一个训练样本是独立的,我们写出它们联合概率密度:
注意:上式中,对应的 y(i) 是已经知道的了哦。其实上式中未知的参数就是 θ 。
其实呢,我们写的上面的公式就是似然函数啦,我们现在要把它最大化。(什么意思呢?这里就要看你对拟然函数的理解了。就是说,随机事件已经发生了,即把每一个样本对应的标签作为随机事件的话,我们已经知道了它们的具体标签,我们就就认为已经发生的事件即是概率最大的事件,所以呢,公式中唯一确定的就是参数 θ 了,我们要需要选择合适的参数θ 使似然函数最大化)
4,最大化似然函数,求出合适的参数θ。
把上面的式子变形为:
然后,我们利用梯度下降法来求参数 θ 。
过程大致是这样的,先对参数θ的求导,即得到梯度,然后呢,再利用梯度下降法的更新原则来更新参数θ就可以了。
求的梯度(注意哦,参数θ=(θ1,θ2,θ3,……)):
更新法则:
5.现在我们已经得到了参θ了,我们就相当于得到了hθ(x) ,然后呢,我们就可以用它进行对测试样本进行分类啦。
softmax分类器
它要解决的问题和上面的差不多,唯一的区别就是类别不局限于两类,而是多类了。
要解决什么样的问题呢??假设有一训练样本集合X = {x1, x2, x3, ……},其中样本 xi 由一系列的属性表示即,xi = (a1, a2, a3,……),并且对于样本集合X中的样本属于类别C = {c1, c2, c3, ……}中的一种。
现在呢,我们有一个测试样本x, 我们根椐上面的知识来推断: 样本x 属于哪种类别呢?
现在开始:
首先说一下指数布族,我也没有花太多的精力放上面哦。
一种形如如下公式的分布即为指数分布族:
第二提一下,一个广义线性模型,其实很多时候,我们很多常见的各种分布都可以用广义线性模型来概括。在一个分布为指数族分布时,我们如何来定义出一个广义线性模型呢?作出三个假设:
1,在给定 x 与 参数θ时,y|x 服从以 η 为变量的指数族的分布:
2, 给定x 时,我们的目标是来预测 T(y)的值。不过在很多时候,T(y) = y;
3, 参数 η =θTx; (为什么呢? 它就是这么设计的,广义线性模型哦)
下面正式推一下softmax回归 (可以用它用分类器的哦)
上面已经说了,对于给定的测试样本 x , 它的输出 有k种可能 (即可以分为k类),我们分别φ1,φ2,φ3,φ4,……,然后呢,我们定义T(y)如下:
并且定义一个运算 I{真} = 1, I{假} = 0; 所以呢,有:
1,上面的(T(y))i = I{y = i} ,其中(T(y))i 表示T(y)的第i 个元素);
2,E[(T(y))i] = P(y = i) = φi.
下面为推导过程:假设以已经φ的情况,把 p(y; φ)写出指数分布族的形式,如下 所示:
注意上面的η是K-1 维的哦,我们现在规定ηk = log(φk/φk) = 0。所以呢, ηi = log(φi / φk),其中i =1,2,……,k)
然后呢,
所以呢,推出:
上面我们假设的φi 已经知道了,其实我们不知道哦,现在我们就推出了怎么去求φi 了。上面的式子表示了怎么由ηi去求θi,这就是softmax函数。对于上式的 ηi = θiT x.(应用上面的第三个假设)。 还因为ηk =0,所以呢,我们又规定了θk = 0。(所以,这里一定注意,θk还是未知数哈,待会用得到这一点)。
其实到这里基本已经完了,因为我们所关心的φi 已经知道怎么去求了。
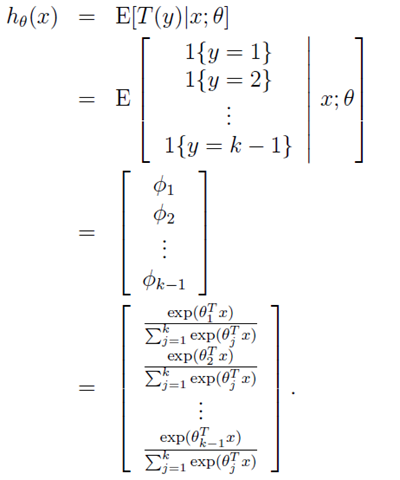
接下来呢,我们来预测T(y)的值哈(看假设的广义线性模型中的第二点哦)
到这里就剩下最后一步了,求拟合参数 θ1,θ2,……,θk-1。 可能会问什么没有θk呢,因为我们上面规定了θk=0. 追根到底是因为:φk =1-(φ1+φ2+ ……+φk-1).
如何求呢,我们写出它的似然函数,然后就可以转变为:用梯主下降或牛顿法等求最值的问题了。它的拟然函数为:
现在呢,我们把参数已经求出来了,可以解决我们的问题了,即给定了一个测试样本,我们估计它属于哪一类。方法是我们分别求出对应的φi, 哪个最大,它就属于哪一类了。
注意:
最后针对这里我们推出的softmax函数中的公式为:
要说明一点,这里的未知数的个数为θ1,θ2,……,θk-1, 而 θk = 0,因为我们只需要求出φ1,φ2, ……,φk-1的值来,我们就能求出φk的值。
而在很多用于分类的神经网络中,最后加的softmax的分类器,它是这样:公式是相同的,但是呢,把θ1,θ2,……,θk-1,θk作为参数,这样有一个什么问题呢,那就是过度参数化了(根本用不着这么多参数嘛),过度参数化会怎样啊? 假如我们对每一个参数θi 减去一个相同的数,变为θi-ψ,然后呢,
发现了,完全不影响假设函数的预测结果哦。
什么意思呢???
所以,在现实中,我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
.




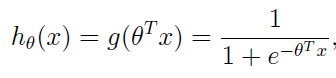
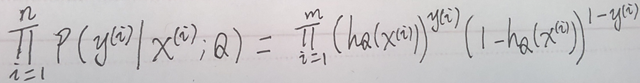
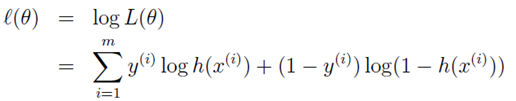
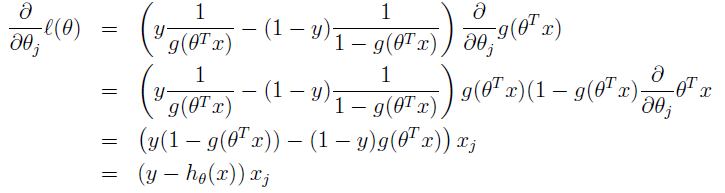

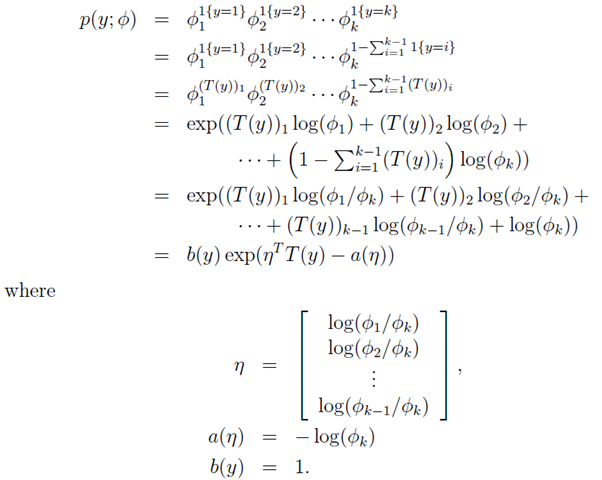
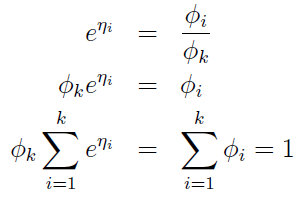
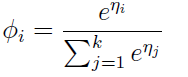
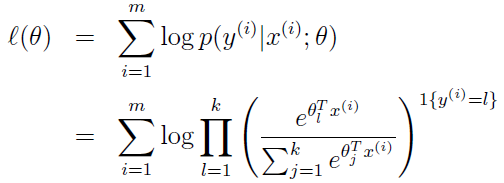
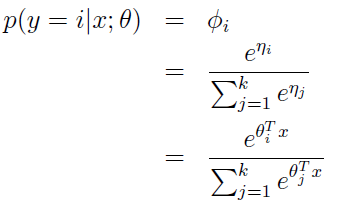
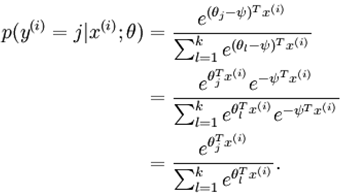



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架