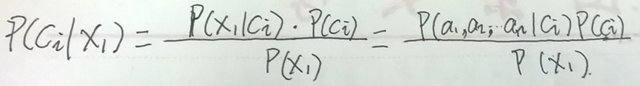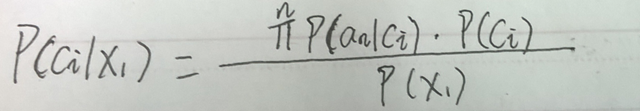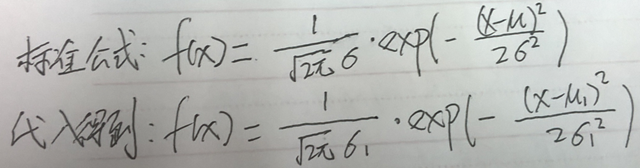朴素贝叶斯分类器

什么是朴素贝叶斯分类器？

首先看朴素两个字，啥意思呢？？它是英文单词 naive 翻译过来的，意思就是简单的，朴素的。（它哪里简单呢，后面会看到的：它假设一个事件的各个属性之间是相互独立的，这样简化了计算过程；这个假设在现实中不太可能成立，但是呢，研究表明对很多分类结果的准确性影响不大哦。） 称为贝叶斯分类器的原因是因为它利用了贝叶斯公式哦；

 

送上贝叶斯公式

首先请看  我写的贝中斯公式相关知识 中的内容，它的公式就是：

P(A|B) = P(B|A) P(A) / P(B)

那它描述了什么呢？  可以这么说： 利用先验概率P(A) 来求 后验概率 P(A|B)。

 

怎么用贝叶斯公式进行分类呢？

设有一个训练样本集合，可以表示为X＝{x1, x2, x3, x4……}，且其中每一个训练样本xi 包括 j 个属性，如 xi = (a1, a2, ……，aj)；  这个训练样本集合可以分为 n 类，如{class1, class2, ……，classn}.

 

现在有一个测试样本x1（我们就假设x1 是独立于训练样本之外的样本哈），如何分类？怎么办？是不是在我们已经 x1 的情况下去求属于每个类别的概率呢，说的学术一点，就是去求类别的后验概率，最后谁的概率最大，它就属于哪类， 公式如下所示：

现在呢，我们把它的”朴素“用上，即我们上面的假设：一个事件的各个属性之间是相互独立的，即 对于xi 事件来说，它的每各属性 a1, a2, a3, ……，aj 是相互独立的，所以上式又可以表示为：

是吧，这样就简单多了。在上式中，对于不同的类 ci, 分母的概率P（x1)是相同的，所以呢， 如果想上 P（ci｜x1) 最大，那么就是让分子最大就可以了。

 

现在的问题是如何求分子中的 P（an|ci）与P（ci)。 这个好说，因为我们有训练样本，我们已经知道了训练样本集合中每个样本所属于的类别了吧。下面我们就通过训练样本集合利用来求哈，具体我们分两类：

1，对于离散的属性来说，我们可以通过统计的方法（用古典概率）哦，即用频率来近拟代替概率哦。

比如，一共1000，000 样本吧，属于类别A的有50，000 个，我们就可以求出 P（A） ＝ 50000 / 1000000 =0.05 。 同样的办法，我们也可以求出 P（an|ci）来吧。 

这里注意：如果其中一个类别的样本也没有怎么办呢？不就是0了吗？我们的做法是分子分母都加1 ，这就叫做 Laplace 平滑处理啦。如上面变为了：P（A） ＝ 50000 +1  / 1000000 +1= 0.05 ，又如属于类别B的为0个样本，这时，P（B） ＝ 0 +1  / 1000000 +n  (n表示一共可以分为n类）。

2.对于连续的数值来说，很多时候把样本中的每个属性看作为为正态分布，这样我们就可以通过训练样本的集合得到正态分布的均值与标准差了吧。然后代入正态分布的标准公式中，得到了函数的高斯密度函数。

举个例子哈，如，假如属性 a1 表示的为身高吧，通过训练样本集合，我们可以得到属于类别A 的所有样本的身高的均值 u1 为与标准差 σ1了吧，现在呢代入正态分布的公式中得到：

得到它以后呢，对于我们要分类的样本 x1 来说，它的身高属性为 h 吧，是不是我们就可以得到了用概率密度  f(h) 来代替  P（a1|ci）了啊。 因为我们反正较的是一个大小，对于用概率密度还是用概率来求都一样，我们只要的谁大谁小。

 

现在我们是不是完成了分类了呢啊，哈哈，这就是朴素贝叶斯分类器。很简单。。

 

注意，我们这么做的前提是，我们假设了”朴素“。现实当然也有很多各个特征属性间往往并不条件独立，而是具有较强的相关性，这样就限制了朴素贝叶斯分类的能力。如果要考虑它们之间的相关性的话，就要用到范围更广的一种算法——贝叶斯网络（又称贝叶斯信念网络或信念网络）了。

 

它的优缺点：

优点：计算速度快； 规则清楚易懂； 独立事件的假设，大多数问题不至于发生太大的偏误；

缺点： 仅适用于类别变量； 仅能应用于分类问题； 假设变量间为独立不影响，因此作用时需要谨慎分析变量间的相关性；