AVL树(自平衡二叉查找树)
了解AVL树之前要先了解二叉查找树(BST),BST查找元素的时间复杂度平均是O(logN),最坏的情况是O(N),所有的元素都接在左子树(或者右子树)就相当于一串链表了。而AVL树会对子树过高的情况进行优化,这里有个平衡因子的概念,当前节点的平衡因子=左子树高度-右子树高度,AVL树的每一个节点的平衡因子的绝对值都是 < 2 的。
当一个新节点插入AVL树 ( 根节点为tree ) 的时候会有四种情况:
假设距离新节点最近的失衡节点为 t ( t 的平衡因子的绝对值达到了2,且距离新节点最近)
1、LL型:新节点在 t1 的左孩子的左子树上,需要对 t 进行一次右旋操作;

2、RR型:新节点在 t 的右孩子的右子树上,需要对 t 进行一次左旋操作;
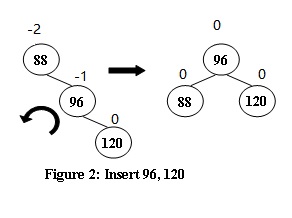
3、LR型:新节点在 t 的左孩子的右子树上,需要先对 t 的左孩子进行一次RR(左旋)操作,然后对 t 进行一次LL(右旋)操作;
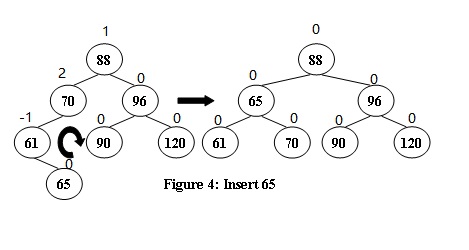
4、RL型:新节点在 t 的右孩子的左子树上,需要先对 t 的右孩子进行一次LL(右旋)操作,然后对 t 进行一次RR(左旋)操作;
AVL树的实现代码如下:
1 #include "pch.h" 2 #include <iostream> 3 #include <queue> 4 #define ElementType int//自定义元素类型 5 using namespace std; 6 typedef struct node *AVLTree; 7 struct node { 8 ElementType key; 9 int Height = 0; 10 AVLTree left = NULL, right = NULL; 11 }; 12 int Height(AVLTree tree);//求树的高度 13 ElementType Max(ElementType a, ElementType b); 14 AVLTree insert(AVLTree tree, ElementType &key);//在AVLTree中插入节点 15 AVLTree LL_Rotation(AVLTree tree);//LL旋转 16 AVLTree RR_Rotation(AVLTree tree);//RR旋转 17 AVLTree LR_Rotation(AVLTree tree);//LR旋转 18 AVLTree RL_Rotation(AVLTree tree);//RL旋转 19 20 void levelTraversal(AVLTree tree);//层序遍历,用于测试 21 22 /*用main函数来测试,给N个不同的数据,插入AVL树中,然后层序输出*/ 23 int main() 24 { 25 int N; 26 ElementType key; 27 AVLTree tree = NULL; 28 scanf("%d", &N); 29 for (int i = 0; i < N; i++) { 30 cin >> key; 31 tree = insert(tree, key); 32 } 33 levelTraversal(tree); 34 } 35 36 AVLTree insert(AVLTree tree, ElementType &key) { 37 if (tree == NULL) { 38 tree = new node(); 39 tree->key = key; 40 } 41 else if (key < tree->key) { 42 tree->left = insert(tree->left, key);//key小于当前节点的值时继续往其左子树递归地插入 43 if (Height(tree->left) - Height(tree->right) >= 2) {//左子树与右子树的高度差达到2的时候就要对当前节点进行旋转,这里由于是递归地执行,保证了平衡因子达到2的节点是最接近插入点的 44 if (key < tree->left->key) 45 tree = LL_Rotation(tree); 46 else 47 tree = LR_Rotation(tree); 48 } 49 } 50 else { 51 tree->right = insert(tree->right, key); 52 if (Height(tree->right) - Height(tree->left) >= 2) { 53 if (key > tree->right->key) 54 tree = RR_Rotation(tree); 55 else 56 tree = RL_Rotation(tree); 57 } 58 } 59 tree->Height = Max(Height(tree->left), Height(tree->right)) + 1;//当前节点的高度为其最大子树的高度+1 60 return tree; 61 } 62 63 AVLTree LR_Rotation(AVLTree tree) { 64 tree->left = RR_Rotation(tree->left); 65 return LL_Rotation(tree); 66 } 67 68 AVLTree RL_Rotation(AVLTree tree) { 69 tree->right = LL_Rotation(tree->right); 70 return RR_Rotation(tree); 71 } 72 73 AVLTree RR_Rotation(AVLTree tree) { 74 AVLTree tree2 = tree->right; 75 tree->right = tree2->left; 76 tree2->left = tree; 77 tree->Height = Max(Height(tree->left), Height(tree->right)) + 1; 78 tree2->Height = Max(Height(tree2->right), tree->Height) + 1; 79 return tree2; 80 } 81 82 AVLTree LL_Rotation(AVLTree tree) { 83 AVLTree tree2 = tree->left; 84 tree->left = tree2->right; 85 tree2->right = tree; 86 tree->Height = Max(Height(tree->left), Height(tree->right)) + 1; 87 tree2->Height = Max(Height(tree->left), tree->Height) + 1; 88 return tree2; 89 } 90 91 int Height(AVLTree tree) { 92 if (tree == NULL) 93 return 0; 94 return tree->Height; 95 } 96 97 ElementType Max(ElementType a, ElementType b) { 98 return a > b ? a : b; 99 } 100 101 void levelTraversal(AVLTree tree) 102 { 103 queue <AVLTree> Q; 104 Q.push(tree); 105 while (!Q.empty()) { 106 AVLTree t = Q.front(); 107 Q.pop(); 108 cout << t->key << " "; 109 if (t->left != NULL) 110 Q.push(t->left); 111 if (t->right != NULL) 112 Q.push(t->right); 113 } 114 }





