刍议线段树 3 （扫描线）

扫描线

扫描线是一种另外的思想，只是其中会运用到线段树以求优化。所以不要将扫描线简单的并为线段树的一个小拓展。

例题：

https://www.luogu.com.cn/problem/P5490

大意：求 $n$ 个四边平行于坐标轴的矩形的面积并。

思路：纵向分割图形

我们考虑把这些纵向矩形分割。
那么，总面积就为分割出的每一段矩形的面积和。

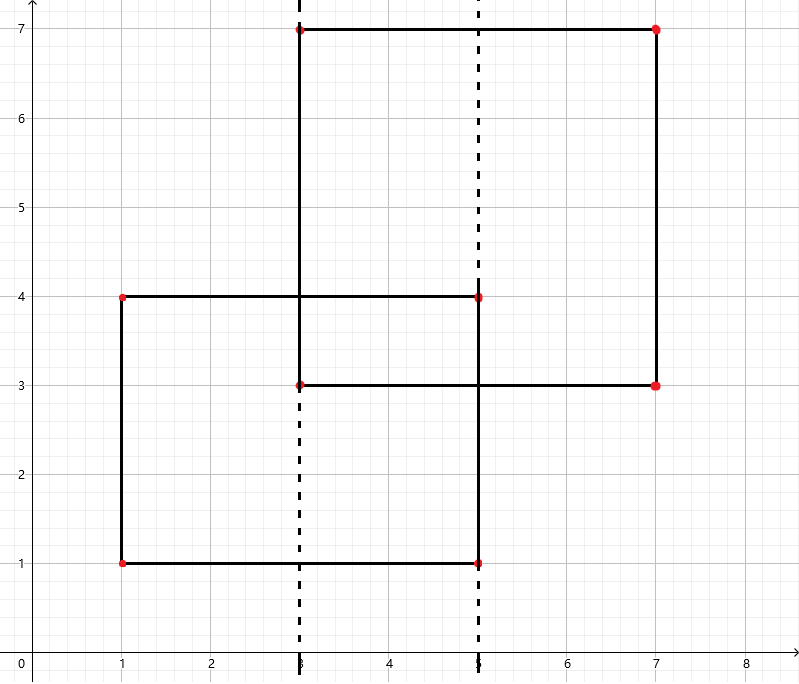
如上图，每扫描到一段，该段面积就是直线上覆盖的长度乘该段的宽度。

同时，我们用一个四元组 $(x,y1,y2,k)$ 表示每条纵向分割线。其中，当 $k=1$ 时表示此边是矩形的左边的边，当 $k=-1$ 时表示此边是矩形右边的边。

线段树则用来维护扫描线上被覆盖的长度（即纵向的长度），每次修改后，更新被覆盖长度。

更新代码如下：

void pushup(int x)
{
	if(t[x].cnt) t[x].len = disx[t[x].r + 1] - disx[t[x].l]; //cnt>0,面积就是直线上覆盖的长度乘该段的宽度。
	else t[x].len = t[x * 2].len + t[x * 2 + 1].len;//cnt=0，面积为其子节点的长度和。
}

这里拉一段李煜东的内容：

在本题我们只关心整个扫描线（线段树根节点）上被覆盖的长度。四元组又成对出现，所以线段树区间修改也是重复出现，这样就没必要下传延时标记，而采用更加简单的做法：在线段树每个节点上另加维护该节点代表的区间被矩形覆盖的长度 $len$，该节点自身被覆盖的次数 $cnt$。对于一个四元组 $(x,y1,y2,k)$，在 $[val(y1),val(y2)-1]$(此处的 $val$ 指的是离散化后 $y$ 的原始值) 上执行区间修改。该区间被线段树划分成 $logN$ 个节点，把这些节点的
$cnt$ 都加 $k$ 。

代码

讲累了，贴代码了

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
ll n;
ll x1,y1,x2,y2;
#define FOR(i,_l,_r) for(ll i=_l;i<=_r;i++)
#define ls p<<1
#define rs p<<1|1
const int N=1e6+5;
int X[N<<1];
ll ans;
struct seg_line
{
	ll l,r;
	ll h;
	ll mark;
}line[N<<1];
bool cmp(seg_line a,seg_line b)
{
	return a.h<b.h;
}
struct srg_tree
{
	ll l,r;
	ll sum;
	ll len;
}tr[N<<2];
void up(int p)
{
	if(tr[p].sum)
		tr[p].len=X[tr[p].r+1]-X[tr[p].l];
	else tr[p].len=tr[ls].len+tr[rs].len;	
}
void build(int p,int l,int r)
{
	tr[p].l=l;tr[p].r=r;
	tr[p].len=tr[p].sum=0;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
	return;
}
void work(int p,ll L,ll R,int c)
{
	ll l=tr[p].l;ll r=tr[p].r;
	if(X[r+1]<=L||X[l]>=R) return;
	if(L<=X[l]&&X[r+1]<=R)
	{
		tr[p].sum+=c;
		up(p);
		return;
	}
	work(ls,L,R,c);
	work(rs,L,R,c);
	up(p);
}
int main()
{
	cin>>n;
	FOR(i,1,n)
	{
		cin>>x1>>y1>>x2>>y2;
		X[2*i-1]=x1;X[2*i]=x2;
		line[2*i-1]=(seg_line){x1,x2,y1,1};
		line[2*i]=(seg_line){x1,x2,y2,-1};
	}
	n<<=1;
	sort(line+1,line+n+1,cmp);
	sort(X+1,X+n+1);
	ll tot=unique(X+1,X+n+1)-X-1;
	build(1,1,tot-1);
	FOR(i,1,n-1)
	{
		work(1,line[i].l,line[i].r,line[i].mark);
		ans+=tr[1].len*(line[i+1].h-line[i].h);
	}
	cout<<ans;
	return 0;
}

本来以为这篇要烂尾了，结果还是糊弄完了，以后本人要先转战 $DP$ ,数据结构暂时放下了。

完结撒花。