Codeforces Round #405 (rated, Div. 2, based on VK Cup 2017 Round 1) D
Description
A tree is an undirected connected graph without cycles. The distance between two vertices is the number of edges in a simple path between them.
Limak is a little polar bear. He lives in a tree that consists of n vertices, numbered 1 through n.
Limak recently learned how to jump. He can jump from a vertex to any vertex within distance at most k.
For a pair of vertices (s, t) we define f(s, t) as the minimum number of jumps Limak needs to get from s to t. Your task is to find the sum off(s, t) over all pairs of vertices (s, t) such that s < t.
The first line of the input contains two integers n and k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ 5) — the number of vertices in the tree and the maximum allowed jump distance respectively.
The next n - 1 lines describe edges in the tree. The i-th of those lines contains two integers ai and bi (1 ≤ ai, bi ≤ n) — the indices on vertices connected with i-th edge.
It's guaranteed that the given edges form a tree.
Print one integer, denoting the sum of f(s, t) over all pairs of vertices (s, t) such that s < t.
6 2
1 2
1 3
2 4
2 5
4 6
20
13 3
1 2
3 2
4 2
5 2
3 6
10 6
6 7
6 13
5 8
5 9
9 11
11 12
114
3 5
2 1
3 1
3
In the first sample, the given tree has 6 vertices and it's displayed on the drawing below. Limak can jump to any vertex within distance at most2. For example, from the vertex 5 he can jump to any of vertices: 1, 2 and 4 (well, he can also jump to the vertex 5 itself).
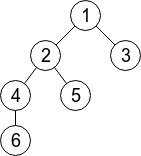
There are 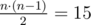 pairs of vertices (s, t) such that s < t. For 5 of those pairs Limak would need two jumps:(1, 6), (3, 4), (3, 5), (3, 6), (5, 6). For other 10 pairs one jump is enough. So, the answer is 5·2 + 10·1 = 20.
pairs of vertices (s, t) such that s < t. For 5 of those pairs Limak would need two jumps:(1, 6), (3, 4), (3, 5), (3, 6), (5, 6). For other 10 pairs one jump is enough. So, the answer is 5·2 + 10·1 = 20.
In the third sample, Limak can jump between every two vertices directly. There are 3 pairs of vertices (s < t), so the answer is 3·1 = 3.
题意:给出一棵树,和最多跳K个数字,f(s,t)表示从s到t需要跳的最少次数,问那么一棵树每两个点跳的次数之和是多少?
解法:如果只跳一次,那每个点经历的次数为这个点的子树节点个数*(n-这个点的子树节点个数),那么K>=2的情况,对于任意两个点的x->y 距离为 深度[x]+深度[y]-2*最近公共祖先深度[z]
dp[v][d%k]表示v为节点开始,深度为d%k的个数,比如2为节点开始,深度为1的有4和5
4在2的子树内,4开始深度为1点为6,我们更新到dp[2][1]内,就是dp[2][1]+=dp[4][1]
sum[v]表示v的子树节点个数
最后答案为ans/n,比如距离为5,最多跳3步,其实是跳(5+1)/3=2次就好了,注释也有解释
(题解好难懂啊,我也不知道说清楚了没)
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const int maxn=300000; 5 ll dp[maxn][10],sum[maxn]; 6 vector<int>q[maxn]; 7 ll vis[maxn]; 8 ll cnt; 9 ll n,k; 10 void dfs(int v,int d,int fa) 11 { 12 dp[v][d%k]=sum[v]=1; 13 //当前子节点就v一个 14 for(int i=0;i<q[v].size();i++) 15 { 16 // cout<<v<<endl; 17 int pos=q[v][i]; 18 if(pos==fa) continue; 19 dfs(pos,d+1,v); 20 for(int x=0;x<k;x++) 21 { 22 for(int y=0;y<k;y++) 23 { 24 int ans=((x+y)%k-(d*2)%k+k)%k; 25 //ans为缺少部分,比如5跳3,少了两步 26 cnt+=((k-ans)%k)*dp[v][x]*dp[pos][y]; 27 //少了两步,为了达成三步,必须多走一步,所以为k-ans,每个点多走k-ans步,相乘 28 } 29 } 30 for(int x=0;x<k;x++) 31 { 32 dp[v][x]+=dp[pos][x]; 33 //子节点记录部分更新到父结点 34 } 35 cnt+=sum[pos]*(n-sum[pos]); 36 //讨论k=1的情况,种数==为pos节点包含子节点*以外的节点 37 sum[v]+=sum[pos]; 38 //将pos包含节点个数更新到父结点 39 40 } 41 } 42 int main() 43 { 44 cin>>n>>k; 45 for(int i=0;i<n-1;i++) 46 { 47 int u,v; 48 cin>>u>>v; 49 q[u].push_back(v); 50 q[v].push_back(u); 51 } 52 dfs(1,0,0); 53 cout<<cnt/k<<endl; 54 return 0; 55 }





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
· 三行代码完成国际化适配,妙~啊~