AtCoder Beginner Contest 054 ABCD题
A - One Card Poker
Time limit : 2sec / Memory limit : 256MB
Score : 100 points
Problem Statement
Alice and Bob are playing One Card Poker.
One Card Poker is a two-player game using playing cards.
Each card in this game shows an integer between 1 and 13, inclusive.
The strength of a card is determined by the number written on it, as follows:
Weak 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < 11 < 12 < 13 < 1 Strong
One Card Poker is played as follows:
- Each player picks one card from the deck. The chosen card becomes the player's hand.
- The players reveal their hands to each other. The player with the stronger card wins the game.
If their cards are equally strong, the game is drawn.
You are watching Alice and Bob playing the game, and can see their hands.
The number written on Alice's card is A, and the number written on Bob's card is B.
Write a program to determine the outcome of the game.
Constraints
- 1≦A≦13
- 1≦B≦13
- A and B are integers.
Input
The input is given from Standard Input in the following format:
A B
Output
Print Alice if Alice will win. Print Bob if Bob will win. Print Draw if the game will be drawn.
Sample Input 1
8 6
Sample Output 1
Alice
8 is written on Alice's card, and 6 is written on Bob's card. Alice has the stronger card, and thus the output should be Alice.
Sample Input 2
1 1
Sample Output 2
Draw
Since their cards have the same number, the game will be drawn.
Sample Input 3
13 1
Sample Output 3
Bob
题意:比较大小
解法:就1需要变换成为14之外,其他不变
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 int main() 5 { 6 int n,m; 7 cin>>n>>m; 8 if(n==1) 9 { 10 n=14; 11 } 12 if(m==1) 13 { 14 m=14; 15 } 16 if(n==m) 17 { 18 cout<<"Draw"; 19 } 20 else if(n<m) 21 { 22 cout<<"Bob"; 23 } 24 else 25 { 26 cout<<"Alice"; 27 } 28 return 0; 29 }
B - Template Matching
Time limit : 2sec / Memory limit : 256MB
Score : 200 points
Problem Statement
You are given an image A composed of N rows and N columns of pixels, and a template image B composed of M rows and M columns of pixels.
A pixel is the smallest element of an image, and in this problem it is a square of size 1×1.
Also, the given images are binary images, and the color of each pixel is either white or black.
In the input, every pixel is represented by a character: . corresponds to a white pixel, and # corresponds to a black pixel.
The image A is given as N strings A1,…,AN.
The j-th character in the string Ai corresponds to the pixel at the i-th row and j-th column of the image A (1≦i,j≦N).
Similarly, the template image B is given as M strings B1,…,BM.
The j-th character in the string Bi corresponds to the pixel at the i-th row and j-th column of the template image B (1≦i,j≦M).
Determine whether the template image B is contained in the image A when only parallel shifts can be applied to the images.
Constraints
- 1≦M≦N≦50
- Ai is a string of length N consisting of
#and.. - Bi is a string of length M consisting of
#and..
Input
The input is given from Standard Input in the following format:
N M A1 A2 : AN B1 B2 : BM
Output
Print Yes if the template image B is contained in the image A. Print No otherwise.
Sample Input 1
3 2 #.# .#. #.# #. .#
Sample Output 1
Yes
The template image B is identical to the upper-left 2×2 subimage and the lower-right 2×2 subimage of A. Thus, the output should be Yes.
Sample Input 2
4 1 .... .... .... .... #
Sample Output 2
No
The template image B, composed of a black pixel, is not contained in the image A composed of white pixels.
题意:问二图是不是一图的子图
解法:数据量不大,暴力
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 char a[100][100],b[100][100]; 5 int n,m; 6 int main() 7 { 8 cin>>n>>m; 9 for(int i=0;i<n;i++) 10 { 11 scanf("%s",a[i]); 12 } 13 for(int i=0;i<m;i++) 14 { 15 scanf("%s",b[i]); 16 } 17 int flag=1; 18 for(int i=0;i<n;i++) 19 { 20 for(int j=0;j<n;j++) 21 { 22 23 if(a[i][j]==b[0][0]) 24 { 25 flag=0; 26 for(int x=0;x<m;x++) 27 { 28 for(int y=0;y<m;y++) 29 { 30 if(a[i+x][j+y]!=b[x][y]) 31 { 32 flag=1; 33 break; 34 } 35 } 36 } 37 } 38 if(flag==0) 39 { 40 cout<<"Yes"; 41 return 0; 42 } 43 } 44 } 45 cout<<"No"; 46 return 0; 47 }
C - One-stroke Path
Time limit : 2sec / Memory limit : 256MB
Score : 300 points
Problem Statement
You are given an undirected unweighted graph with N vertices and M edges that contains neither self-loops nor double edges.
Here, a self-loop is an edge where ai=bi(1≤i≤M), and double edges are two edges where (ai,bi)=(aj,bj) or (ai,bi)=(bj,aj)(1≤i<j≤M).
How many different paths start from vertex 1 and visit all the vertices exactly once?
Here, the endpoints of a path are considered visited.
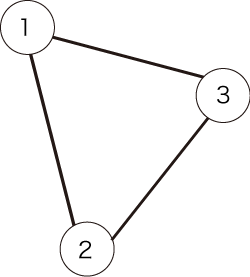
For example, let us assume that the following undirected graph shown in Figure 1 is given.
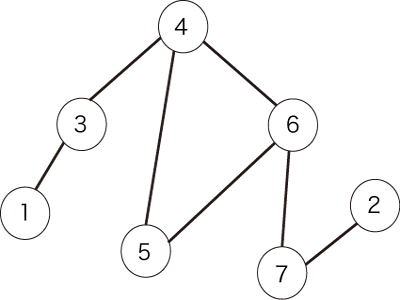
Figure 1: an example of an undirected graph
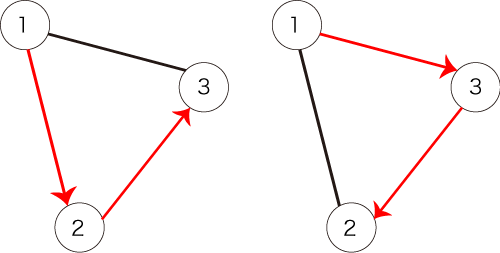
The following path shown in Figure 2 satisfies the condition.
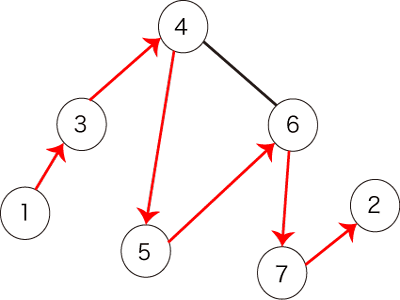
Figure 2: an example of a path that satisfies the condition
However, the following path shown in Figure 3 does not satisfy the condition, because it does not visit all the vertices.
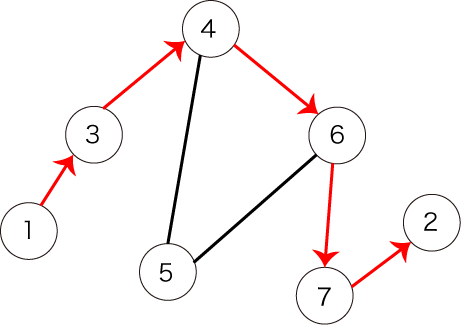
Figure 3: an example of a path that does not satisfy the condition
Neither the following path shown in Figure 4, because it does not start from vertex 1.
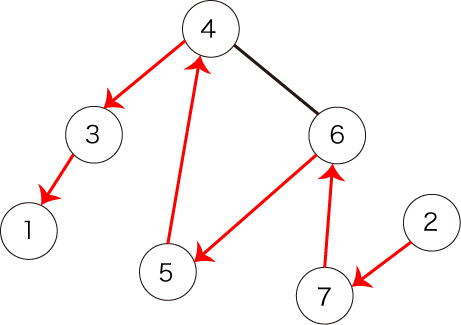
Figure 4: another example of a path that does not satisfy the condition
Constraints
- 2≦N≦8
- 0≦M≦N(N−1)⁄2
- 1≦ai<bi≦N
- The given graph contains neither self-loops nor double edges.
Input
The input is given from Standard Input in the following format:
N M a1 b1 a2 b2 : aM bM
Output
Print the number of the different paths that start from vertex 1 and visit all the vertices exactly once.
Sample Input 1
3 3 1 2 1 3 2 3
Sample Output 1
2
The given graph is shown in the following figure:
The following two paths satisfy the condition:
Sample Input 2
7 7 1 3 2 7 3 4 4 5 4 6 5 6 6 7
Sample Output 2
1
This test case is the same as the one described in the problem statement.
题意:求从1开始到每个点的路径有多少种
解法:数据量不大,可以是由1开始的全排列,看是否符合
或者从1开始搜索,能够访问所有点就加一
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=2002; 4 vector<int>m[maxn]; 5 int n,p; 6 int sum; 7 int vis[maxn]; 8 void dfs(int cot,int num) 9 { 10 if(num==n) 11 { 12 sum++; 13 return; 14 } 15 for(int i=0;i<m[cot].size();i++) 16 { 17 if(vis[m[cot][i]]==0) 18 { 19 vis[m[cot][i]]=1; 20 dfs(m[cot][i],num+1); 21 vis[m[cot][i]]=0; 22 } 23 } 24 } 25 int main() 26 { 27 cin>>n>>p; 28 for(int i=1;i<=p;i++) 29 { 30 int v,u; 31 cin>>v>>u; 32 m[v].push_back(u); 33 m[u].push_back(v); 34 } 35 sum=0; 36 vis[1]=1; 37 dfs(1,1); 38 cout<<sum<<endl; 39 return 0; 40 }
D - Mixing Experiment
Time limit : 2sec / Memory limit : 256MB
Score : 400 points
Problem Statement
Dolphin is planning to generate a small amount of a certain chemical substance C.
In order to generate the substance C, he must prepare a solution which is a mixture of two substances A and B in the ratio of Ma:Mb.
He does not have any stock of chemicals, however, so he will purchase some chemicals at a local pharmacy.
The pharmacy sells N kinds of chemicals. For each kind of chemical, there is exactly one package of that chemical in stock.
The package of chemical i contains ai grams of the substance A and bi grams of the substance B, and is sold for ci yen (the currency of Japan).
Dolphin will purchase some of these packages. For some reason, he must use all contents of the purchased packages to generate the substance C.
Find the minimum amount of money required to generate the substance C.
If it is not possible to generate the substance C by purchasing any combination of packages at the pharmacy, report that fact.
Constraints
- 1≦N≦40
- 1≦ai,bi≦10
- 1≦ci≦100
- 1≦Ma,Mb≦10
- gcd(Ma,Mb)=1
- ai, bi, ci, Ma and Mb are integers.
Input
The input is given from Standard Input in the following format:
N Ma Mb a1 b1 c1 a2 b2 c2 : aN bN cN
Output
Print the minimum amount of money required to generate the substance C. If it is not possible to generate the substance C, print -1 instead.
Sample Input 1
3 1 1 1 2 1 2 1 2 3 3 10
Sample Output 1
3
The amount of money spent will be minimized by purchasing the packages of chemicals 1 and 2.
In this case, the mixture of the purchased chemicals will contain 3 grams of the substance A and 3 grams of the substance B, which are in the desired ratio: 3:3=1:1.
The total price of these packages is 3 yen.
Sample Input 2
1 1 10 10 10 10
Sample Output 2
-1
The ratio 1:10 of the two substances A and B cannot be satisfied by purchasing any combination of the packages. Thus, the output should be -1.
题意:求能够配出Ma:Mb的比例药剂最小花费
解法:dp[i][j][z]中i表示已经考虑了第i种配方,j表示已经配了a的容量,z表示已经配了b的容量,先初始化他们的最大值,dp[0][0][0]=0
dp[i+1][j][z]=min(dp[i][j][z],dp[i+1][j][z]) 没有加i配方进去
dp[i+1][j+a[i]][z+b[i]]=min(dp[i+1][j+a[i]][z+b[i]],dp[i][j][z]+c[i]) 加了配方i进去
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn = 220; 4 int a[maxn],b[maxn],c[maxn]; 5 int ans,n,k; 6 int x,y; 7 int Ma,Mb; 8 int inf=2000000; 9 int dp[50][500][500]; 10 int main() 11 { 12 cin>>n>>Ma>>Mb; 13 for(int i=0;i<n;i++) 14 { 15 cin>>a[i]>>b[i]>>c[i]; 16 } 17 for(int i=0;i<=40;i++) 18 { 19 for(int j=0;j<=400;j++) 20 { 21 for(int z=0;z<=400;z++) 22 { 23 dp[i][j][z]=inf; 24 } 25 } 26 } 27 dp[0][0][0]=0; 28 for(int i=0;i<n;i++) 29 { 30 for(int j=0;j<=400;j++) 31 { 32 for(int z=0;z<=400;z++) 33 { 34 if(dp[i][j][z]==inf) continue; 35 dp[i+1][j][z]=min(dp[i][j][z],dp[i+1][j][z]); 36 dp[i+1][j+a[i]][z+b[i]]=min(dp[i+1][j+a[i]][z+b[i]],dp[i][j][z]+c[i]); 37 } 38 } 39 } 40 int Minx=inf; 41 for(int i=1;i<=400;i++) 42 { 43 for(int j=1;j<=400;j++) 44 { 45 if(i*Mb==j*Ma) 46 { 47 Minx=min(Minx,dp[n][i][j]); 48 } 49 } 50 } 51 if(Minx==inf) 52 { 53 cout<<"-1"; 54 } 55 else 56 { 57 cout<<Minx; 58 } 59 return 0; 60 }




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
· 三行代码完成国际化适配,妙~啊~
2016-02-12 Educational Codeforces Round 7 B
2016-02-12 Educational Codeforces Round 7 A