广义后缀自动机（广义 SAM）学习笔记

开 CF 开到了一道广义 SAM，决定来学一学。
发现网上确实充斥着各种各样的伪广义 SAM，也看到了前人反复修改假板子的过程，所以试着来整理一下这堆奇奇怪怪的问题。
当然本文的代码也不保证百分百正确，有误请指出（？

前置知识

后缀自动机 (SAM) 的构造及应用
其实想写在一起的，但因为太长就把这两篇文章拆开了。本文所述的「上文」若无法在本文中找到，则均指代该博客。

概述

广义 SAM 用于解决多模式串上的子串相关问题。
它对多个字符串建立出一个 SAM，或者说本质是对多个字符串形成的一棵 Trie 树建立 SAM。
其实大部分能够使用普通 SAM 解决的字符串问题都可以扩展到 Trie 树上，并使用广义 SAM 处理。

这里要注意，题目给出多个字符串和直接给出一棵 Trie 树是不同的。后者仅保证了 Trie 树的节点数，但没有保证所有模式串的总长度。
设 \(n\) 为 Trie 的节点数，这种情况下的字符串总长上界可以达到 \(n^2\)，可以通过在一条链的链底挂一个菊花构造得到。
一些广义 SAM 写法的时间复杂度基于字符串总长而非节点个数，但第二种给出字符串的方式远不如第一种常见。因此这些写法也是正确的广义 SAM，只不过不适用于少量直接给出 Trie 的题目。
我们定义后文中与时间复杂度相关的部分，Trie 的节点数为 \(n\)，字符串总长为 \(m\)。

定义与概念的拓展

在把 SAM 搬到 Trie 上之前，我们要先把单串 SAM 相关的定义拓展到 Trie 上。

后缀

首先定义 Trie 树为 \(S\)，\(S_{x,y}\) 表示 Trie 上从点 \(x\) 到点 \(y\) 的路径组成的字符串。
那么它的所有后缀可以表示为 \(\{S_{x,y} \mid y\in \text{subtree}(x), y \text{ is leaf}\}\)。
广义 SAM 压缩的就是该集合内的后缀。

endpos 集合

更改了后缀的定义，一个字符串 \(\text{endpos}\) 集合的定义也随之改变：\(\text{endpos}(t)=\{y\mid y\in \text{subtree}(x),S_{x,y}=t\}\)。

后缀链接 link

在新的 \(\text{endpos}\) 定义下，可以沿用后缀链接 \(\text{link}\) 的原定义。

那么我们根据新的定义对 Trie 构建出的 SAM 结构，就可以称作广义 SAM。

常见的伪广义 SAM

对于此类问题，通常有这样几种做法：

在每两个串之间添加一个特殊字符，把所有串连接成一个大串，再对其建单串 SAM。
每次添加一个新串前将 \(lst\) 改为 \(1\)（初始节点），在原 SAM 的基础上继续构建。
广义 SAM。

但前两种都是常见的伪广义 SAM，我们依次对它们的正确性进行分析。

连成一个串建 SAM

结论：仅在字符串个数很少时能够保证复杂度。
这样做可以解决一部分问题，例如前文所述 SAM 的最后一个例题 LCS2 - Longest Common Substring II。
但这种方法的瓶颈在于所有的「特殊字符」两两不能相同，否则不能对不同的子串进行区分。这造成了当题目仅保证字符串总长而不保证个数时，将会需要大量的特殊字符。而 SAM 的线性复杂度是基于字符集大小为常数这一条件的。
因此这种方法造成了 SAM 的字符集不再为常数，时间复杂度无法保证。对于此题，可以这么做是因为题目保证了字符串数量不超过 \(10\)。

每次将 lst 置为 1

结论：时间复杂度正确，但会出现存在空节点的问题。
在字符串总长有保证时，我们可以类比单串 SAM 的证明方法来证明它的线性复杂度。
但这种做法会出现所谓的「空节点」问题，这也是各种写假的广义 SAM 的共同错误。
由于该方法几乎不需要对单串 SAM 进行改动，比较好写，在很多不会出现正确性问题的题目中经常被使用。

故上述两种方法都有其局限性，学习正确的广义 SAM 是必要的。

空节点问题

上文说过，各种写假的广义 SAM 会出现空节点。
先以已经提到的每次将 \(lst\) 置为 \(0\) 为例，看看为什么会这样。
举一个简单的例子，假设我们已经对 \(\mathtt{ab}\) 构建了 SAM：

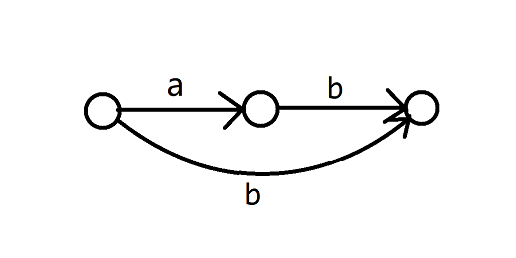
现在加入字符串 \(\mathtt{b}\)，你会发现你新建了一个节点，把它的 \(\text{link}\) 连向了 \(0\)（蓝色是 \(\text{link}\) 边），但实际上没有任何一条转移边连向它。

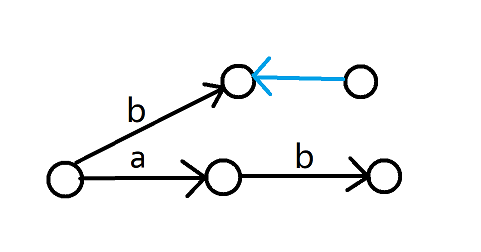
这样的空节点在匹配子串时不会影响正确性，也不影响时间复杂度，仅作为一个自动机而言并没有问题。
但它破坏了 SAM 用最小的状态数储存所有子串的性质，会影响到 \(fail\) 树的子树 \(siz\) 计算，在某些需要用到相关信息的题目中出现错误。
下文会对各种本身正确但由于实现问题造成的假广义 SAM 也给出分析。

bfs 离线构建

离线构建是指我们先读入所有字符串，对它们构建出 Trie 树，再基于 Trie 树构建 SAM 的写法，分为 dfs 与 bfs 两种实现方式。

bfs 实现

首先我们要做的事情是对字符串建出 Trie。

struct trie{int fa,c,s[26];} tr[N];
int idx=1;
il void ins(char *s) 
{
    int len=strlen(s+1),now=1;
    for(int i=1;i<=len;i++) 
    {
        int &to=tr[now].s[s[i]-'a'];
        if(!to) to=++idx,tr[to].fa=now,tr[to].c=s[i]-'a'; now=to;
    }
}

然后考虑 SAM 的构造。因为每次是把父亲节点在 SAM 上的位置作为 \(lst\) 构建新的节点，我们需要对每个 Trie 上的节点记录它在 SAM 上对应的节点编号。

我们令点 \(x\) 在 SAM 上对应的节点编号为 \(pos_x\)。同时，为方便记录这个 \(pos\)，我们对 insert 函数稍作改动，给它加上返回值，返回新添加的节点编号：

il int insert(int c,int lst)
{
    int p=lst,np=lst=++tot; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return np;
}

那么我们 bfs 到点 \(x\) 时，把 \(pos_{fa_x}\) 作为 \(lst\)，向 SAM 插入 \(fa_x\) 到 \(x\) 这条边上的字符 \(c\)，并令 \(pos_x\) 为 insert 函数的返回值即可。
由此可以写出 bfs 的离线构建：

int pos[N];
il void build()
{
    queue<int> q;
    for(int i=0;i<26;i++) if(tr[1].s[i]) q.push(tr[1].s[i]);
    pos[1]=1;
    while(!q.empty())
    {
        int u=q.front(); q.pop();
        pos[u]=insert(tr[u].c,pos[tr[u].fa]);
        for(int i=0;i<26;i++) if(tr[u].s[i]) q.push(tr[u].s[i]);
    }
}

如果不考虑空节点问题，每次将 \(lst\) 置为 \(0\) 的方法是比较容易理解的。
而离线 bfs 构造实际上就是通过 Trie 树的性质压缩了原来的多个字符串，这样做相同的前缀不再需要多次插入，其余的和上面的方法本质相同。

为什么 bfs 不会有空节点

考虑上面的做法出现了空节点是哪里的问题。
我们在 \(lst\) 已经有一条 \(c\) 的转移边的情况下，试图再给 \(lst\) 连新的 \(c\) 边，就会出现加了一个节点，但加的转移都跑到了原来 \(lst\) 连向的那个点。这个新加的点就变成了只有 \(\text{link}\) 的空壳。
而 bfs 的过程不同，它是按照字符串的长度从小到大一层层加点的。也就是说，我们试图给 \(fa_x\) 加一个 \(c\) 的转移的时候，它之前不可能已经有一个 \(c\) 边。
这个可以反证，如果 \(fa_x\) 已经有连向 \(c\) 的转移，说明 \(fa_x\) 已经有一个边为字符 \(c\) 的儿子。显然合法的 Trie 中，一个节点不会有边上字符相同的两个不同儿子，故该情况不成立。
综上，不在 insert 函数中加特判的 bfs 写法是正确的，因为它保证了不会出现空点。

时间复杂度证明

bfs 写法的时间复杂度为 \(O(n)\)，即 Trie 的节点数。
这是因为 bfs 的性质保证了 SAM 原有的时间复杂度证明仍然成立，参见前文 SAM 的复杂度证明。

dfs 离线构建

错误的 dfs 实现

我们似乎可以用同样的方式来实现 dfs 离线构建，写出如下的代码。

int pos[N];
il void dfs(int u)
{
    for(int i=0;i<26;i++)
    {
        int v=tr[u].s[i];
        if(v) pos[v]=insert(i,pos[u]),dfs(v);
    }
}

但这种不加任何特判的 dfs 写法是错的。在模板题增加输出节点个数的要求后，它甚至无法通过样例。

为什么 dfs 会产生空节点

之前我们证明了 bfs 的正确性，为什么换成 dfs 就错了呢？
回想一下，我们的正确性证明是基于 “试图给 \(fa_x\) 加一个 \(c\) 的转移的时候，它之前不可能已经有一个 \(c\) 边” 这条 bfs 独有的性质的。
dfs 时显然没有这条保证，因此会和 \(lst\) 置为 \(0\) 的做法出一样的问题。

更直观但不那么严谨的理解是，假设我们对 \(\mathtt{ab}\) 和 \(\mathtt{b}\) 建 Trie 然后 dfs，你会发现 Trie 建了个寂寞，它的算法过程跟 \(lst\) 置为 \(1\) 没有任何本质区别。

正确的 dfs 实现

我们需要通过特判已有转移边的情况来规避以上问题。

il int insert(int c,int lst)
{
    if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];} //1
    int p=lst,np=++tot,flag=0; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    if(p==lst) flag=1,np=0,tot--;  //2
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return flag?nq:np;  //3
}

注意到，这份代码的 insert 过程和原来的区别是新增了注释处的三句特判。接下来对它们依次进行解释。

if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];} //1

这句话特判的是新加的串已经作为原来的子串出现过的情况，即 \(lst\) 已经有一条 \(c\) 的转移，而且这个转移是连续的。
此时我们什么也不用做，新加入的点所在的 \(pos\) 就是当前 \(lst\) 连边指向的点。

if(p==lst) flag=1,np=0,tot--;  //2

另外一种会出现空节点的情况是 \(lst\) 有 \(c\) 的转移，但这个转移不是连续的。
这表明在加入字符 \(c\) 后，应当有一部分后缀被拆出来变成新的状态，但我们只应新建这个新状态的节点，不应新建 \(lst\) 连向 \(c\) 的节点。还是以文章开头那两个字符串为例。

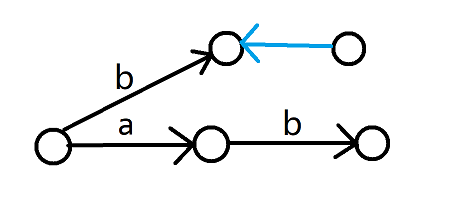
我们在插入第二个串时就是特判 2 的情况，这时候不应该新建一个节点。但是貌似我们在做这个判断前已经新建过了。不过好在 \(np\) 里面啥都没有，把加过的 \(tot\) 减回去就好啦 qwq。
同时因为没有新建节点，也不应该有 \(np\)，更不应该有 \(\text{link}(np)\)。所以为了避免后面意外修改这个位置的值，要把 \(np\) 置为 \(0\)。（我的 SAM 板子是从 \(1\) 开始编号，\(0\) 号节点没有任何作用。）

return flag?nq:np;  //3

这句是容易理解的，没有新建 \(np\) 但新建了 \(nq\)，就返回 \(nq\)。

至此我们写出了正确的离线 dfs 板子。

dfs 的复杂度证明

与 bfs 做法不同，dfs 做法时间复杂度是 \(O(m)\)，即字符串总长度。它不能用于直接给出 Trie 树的题目。
这是因为我们原来在证 SAM 复杂度时的条件不适用了，SAM 每次都会在原来的 \(lst\) 后面加节点，并从 \(lst\) 开始跳 \(\text{link}\) 树。这保证了被重定向的边不会再次被重定向。
而 dfs 的过程中并没有这样的保证，一条边可以随着多个字符串的加入被重定向多次。

举一个直观的例子，我们有这样一棵 Trie：

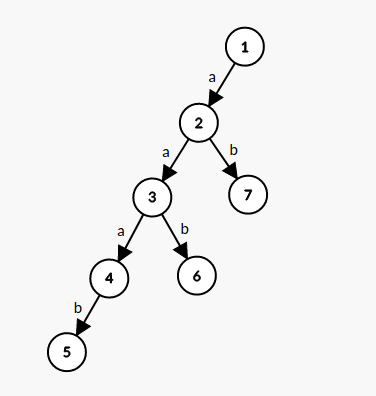
现在 dfs 完了点 \(1\sim 5\)，获得了一个长这样的 SAM：

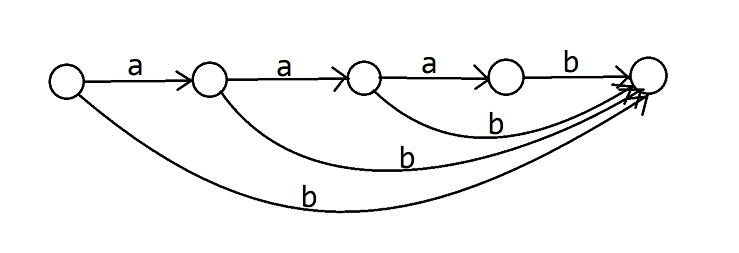
然后我们 dfs 点 \(6\)，发现它改变了 \(\mathtt{b,ab,aab}\) 的 \(\text{endpos}\) 集合，这些转移都需要拆出来。

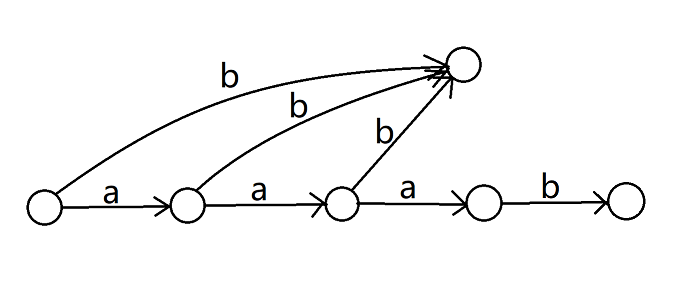
再继续 dfs 点 \(7\)，又改变了 \(\mathtt{b,ab}\) 的 \(\text{endpos}\)，需要把之前拆出来过的转移再拆出来：

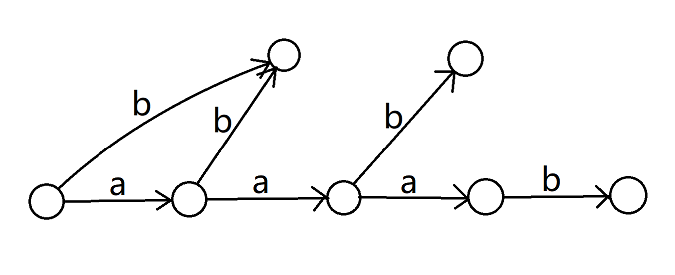
可以看出它的时间复杂度并不是 Trie 树的节点数，因此 Trie 的结构对 dfs 的复杂度没有什么优化作用。
稍加思考的话，可以发现这样的做法和每次把 \(lst\) 置为 \(1\)，再跑加特判版本的 SAM 没有本质区别。它的时间复杂度是字符串总长。

在线构建

在线构建广义 SAM，就是不预先建出 Trie 树，直接每次将 \(lst\) 置为 \(1\)，依次在线插入字符串。
之前所说的错误做法是指不带任何特判的 SAM，而我们在 dfs 中已经为 insert 函数增加了保证它不出现问题的特判。
那么我们还要 dfs 干什么呢？直接用这个加过特判的 insert 函数在线构造，重复的前缀会被特判处理到，其实就变成对的了。它的时间复杂度是字符串总长 \(O(m)\)。

至此我们介绍完了广义 SAM 常见的离线和在线写法。

应用

在实际应用中，SAM 的大部分结论在广义 SAM 中依然成立。

P6139 【模板】广义后缀自动机（广义 SAM）

回到本题。根据 SAM 的已有结论，每个节点包含的不同子串数为 \(\text{len}(x)-\text{len}(\text{link}(x))\)。
所以构建出广义 SAM 后统计答案即可。

离线 bfs 版

#include<bits/stdc++.h>
#define il inline
using namespace std;
il long long read()
{
    long long xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9')
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=2e6+5;
struct trie{int fa,c,s[26];} tr[N];
int idx=1;
il void ins(char *s) 
{
    int len=strlen(s+1),now=1;
    for(int i=1;i<=len;i++) 
    {
        int &to=tr[now].s[s[i]-'a'];
        if(!to) to=++idx,tr[to].fa=now,tr[to].c=s[i]-'a'; now=to;
    }
}
struct SAM{int fa,len,s[26];} d[N];
int tot=1;
il int insert(int c,int lst)
{
    int p=lst,np=lst=++tot; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return np;
}
int pos[N];
il void build()
{
    queue<int> q;
    for(int i=0;i<26;i++) if(tr[1].s[i]) q.push(tr[1].s[i]);
    pos[1]=1;
    while(!q.empty())
    {
        int u=q.front(); q.pop();
        pos[u]=insert(tr[u].c,pos[tr[u].fa]);
        for(int i=0;i<26;i++) if(tr[u].s[i]) q.push(tr[u].s[i]);
    }
}
char s[N];
int main()
{
    int n=read();
    for(int i=1;i<=n;i++) scanf("%s",s+1),ins(s);
    build();
    long long ans=0;
    for(int i=2;i<=tot;i++) ans+=d[i].len-d[d[i].fa].len;
    printf("%lld\n%d\n",ans,tot);
    return 0;
}

离线 dfs 版

#include<bits/stdc++.h>
#define il inline
using namespace std;
il long long read()
{
    long long xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9')
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=2e6+5;
struct trie{int fa,c,s[26];} tr[N];
int idx=1;
il void ins(char *s) 
{
    int len=strlen(s+1),now=1;
    for(int i=1;i<=len;i++) 
    {
        int &to=tr[now].s[s[i]-'a'];
        if(!to) to=++idx,tr[to].fa=now,tr[to].c=s[i]-'a'; now=to;
    }
}
struct SAM{int fa,len,s[26];} d[N];
int tot=1;
il int insert(int c,int lst)
{
    if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];}
    int p=lst,np=++tot,flag=0; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    if(p==lst) flag=1,np=0,tot--;
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return flag?nq:np;
}
int pos[N];
il void dfs(int u)
{
    for(int i=0;i<26;i++)
    {
        int v=tr[u].s[i];
        if(v) pos[v]=insert(i,pos[u]),dfs(v);
    }
}
char s[N];
int main()
{
    int n=read();
    for(int i=1;i<=n;i++) scanf("%s",s+1),ins(s);
    pos[1]=1,dfs(1);
    long long ans=0;
    for(int i=2;i<=tot;i++) ans+=d[i].len-d[d[i].fa].len;
    printf("%lld\n%d\n",ans,tot);
    return 0;
}

在线版

#include<bits/stdc++.h>
#define il inline
using namespace std;
il long long read()
{
    long long xr=0,F=1; char cr;
    while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
    while(cr>='0'&&cr<='9')
        xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
    return xr*F;
}
const int N=2e6+5;
struct SAM{int fa,len,s[26];} d[N];
int tot=1,pos[N];
il int insert(int c,int lst)
{
    if(d[lst].s[c]&&d[d[lst].s[c]].len==d[lst].len+1) {return d[lst].s[c];} 
    int p=lst,np=++tot,flag=0; d[np].len=d[p].len+1;
    for(;p&&!d[p].s[c];p=d[p].fa) d[p].s[c]=np;
    if(!p) {d[np].fa=1;return np;}
    int q=d[p].s[c];
    if(d[q].len==d[p].len+1) {d[np].fa=q;return np;}
    if(p==lst) flag=1,np=0,tot--;  
    int nq=++tot; d[nq]=d[q],d[nq].len=d[p].len+1;
    d[q].fa=d[np].fa=nq;
    for(;p&&d[p].s[c]==q;p=d[p].fa) d[p].s[c]=nq;
    return flag?nq:np;  
}
char s[N];
int main()
{
    int n=read();
    for(int i=1;i<=n;i++) 
    {
        scanf("%s",s+1);
        int len=strlen(s+1); pos[0]=1;
        for(int j=1;j<=len;j++) pos[j]=insert(s[j]-'a',pos[j-1]);
    }
    long long ans=0;
    for(int i=2;i<=tot;i++) ans+=d[i].len-d[d[i].fa].len;
    printf("%lld\n%d\n",ans,tot);
    return 0;
}

其他例题

待更新。

参考资料

《后缀自动机在字典树上的拓展》by 刘研绎
【学习笔记】字符串—广义后缀自动机 by 辰星凌
悲惨故事长文警告关于广义 SAM 的讨论 by ix35

坑还没填，但是先撒花 >w<

posted @ 2023-10-26 19:21 樱雪喵阅读(656) 评论(1) 编辑收藏举报

刷新页面返回顶部

樱雪喵的小窝qwq