Codeforces Round 905 Div 1 (CF1887)
A1. Dances (Easy version)
把 \(a,b\) 序列都从小到大排序,\(a\) 贪心删大的,\(b\) 贪心删小的,二分答案并 \(O(n)\) \(\text{check}\)。
Code
const int N=1e5+5;
int T,n,m;
int a[N],b[N];
il bool check(int mid)
{
for(int i=1,j=mid+1;i<=n-mid;i++,j++) if(a[i]>=b[j]) return 0;
return 1;
}
int main()
{
T=read();
while(T--)
{
n=read(),m=read();
a[1]=1;
for(int i=2;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++) b[i]=read();
sort(a+1,a+n+1),sort(b+1,b+n+1);
int l=0,r=n;
while(l<r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
printf("%d\n",l);
}
return 0;
}
A2. Dances (Hard Version)
日常给大家提供乐子。
Solution 1
现在的限制变成了 \(m\le 10^9\),肯定不能一个一个求答案。但是发现我们只关心这个 \(a_1\) 和 \(a,b\) 中其余的每个元素的大小关系。也就是说我们只要枚举 \(4\times 10^5\) 种大小关系,对他们分别求解就可以得到所有答案了。
原来对一个给定序列求答案的时间复杂度是 \(O(n\log n)\),考虑优化这个过程。
同样二分删掉的数量 \(mid\),设 \(a_1=x\),\(a\) 序列排序时不包含 \(a_1\)。
那么把 \(x\) 插进 \(a\) 的对应位置,需要判断的区间可以分成 \(3\) 段:\(a\) 序列中在 \(x\) 前的部分,\(x\) 的位置,\(a\) 序列中在 \(x\) 后的部分。
已经有两个 \(\log\) 了,需要 \(O(1)\) 地判断 \([a_l,a_r]\) 与 \([b_L,b_R]\) 对应起来是否合法。
设 \(lst_i\) 表示第一个比 \(b_i\) 小的位置与当前位置的差值。换句话说,取最大的 \(j\) 使 \(a_j<b_i\),令 \(lst_i= j-i\)。那么 \([a_l,a_r]\) 与 \([b_L,b_R]\) 合法的判断条件就是 \(L-l\le \min\{lst_L,\dots,lst_R\}\)。使用 ST 表维护。
时间复杂度 \(O(n \log^2 n)\)。
我也不知道我怎么 5min 想到这个做法调了 1h 的,所以写出来给大家看看乐子。
Solution 2
发现答案只有两种,我们先把 \(a_{2,\dots,n}\) 跟 \(b\) 匹配。
现在加了一个数,要么以上匹配还是合法,要么变不合法了,那就把新加的那个删掉,答案增加 \(1\)。于是就做完了。
Code
#define int long long
const int N=2e5+5;
int T,n,m;
int a[N],b[N],d[N],L[N],tot;
int st[20][N];
il bool check(int l,int r,int L,int R)
{
if(l>r) return 1;
int len=__lg(R-L+1);
int mn=min(st[len][L],st[len][R-(1<<len)+1]);
if(mn<l-L) return 0;
return 1;
}
il bool Check(int mid,int x)
{
int pos=lower_bound(a+1,a+n,x)-a;
if(pos>n-mid&&mid) return check(1,n-mid,mid+1,n);
bool flag1=check(1,pos-1,mid+1,mid+pos-1);
bool flag2=x<b[mid+pos];
bool flag3=check(pos,n-mid-1,mid+pos+1,n);
return flag1&&flag2&&flag3;
}
il int Solve(int x)
{
int l=0,r=n;
while(l<r)
{
int mid=(l+r)>>1;
if(Check(mid,x)) r=mid;
else l=mid+1;
}
return l;
}
void solve()
{
tot=1;
n=read(),m=read(); d[1]=m; d[++tot]=1;
for(int i=1;i<n;i++) a[i]=read(),d[++tot]=a[i];
for(int i=1;i<=n;i++) b[i]=read(),d[++tot]=b[i];
sort(a+1,a+n),sort(b+1,b+n+1),sort(d+1,d+tot+1);
for(int i=1;i<=n;i++)
{
L[i]=lower_bound(a+1,a+n,b[i])-a-1-i;
// cerr<<"L[i] "<<i<<" "<<L[i]<<endl;
st[0][i]=L[i];
}
for(int i=1;i<=__lg(n);i++)
for(int j=1;j<=n-(1<<i)+1;j++) st[i][j]=min(st[i-1][j],st[i-1][j+(1<<i-1)]);
int ans=0;
for(int i=1;i<=tot;i++)
{
if(d[i]!=d[i-1]) ans+=Solve(d[i]);
if(d[i]==m) break;
if(i!=tot&&d[i+1]-d[i]>1) ans+=(d[i+1]-d[i]-1)*Solve(d[i]+1);
}
printf("%lld\n",ans);
}
signed main()
{
int T=read();
while(T--) solve();
}
B. Time Travel
因为时间和时间不好区分,我们不妨令 \(a_i\) 叫时间,\(i\) 叫日期。
设 \(dis_i\) 表示到达点 \(i\) 的最早日期。对每条边记录它所属的时间。
把每个 \(i\) 按 \(a_i\) 分组,就可以二分出在当前 \(dis_u\) 下 \(u\to v\) 这条边可通行的最早日期。
把这个当作边权跑 dijkstra 就行了,双 \(\log\) 但是跑得挺快。
Code
const int N=2e5+5,inf=1e9;
#define pii pair<int,int>
#define fi first
#define se second
int n,t,k,a[N];
map<pii,int> mp;
struct edge{int nxt,to,id;} e[N<<1];
int head[N],cnt=1;
il void add(int u,int v,int id) {e[++cnt]={head[u],v,id};head[u]=cnt;}
vector<int> tim[N],nxt[N];
int dis[N];
il int get(int nowt,int id)
{
auto ans=upper_bound(nxt[id].begin(),nxt[id].end(),nowt);
if(ans==nxt[id].end()) return inf;
else return *ans;
}
int main()
{
n=read(),t=read();
for(int i=1;i<=t;i++)
{
int x=read();
for(int j=1;j<=x;j++)
{
int u=read(),v=read();
add(u,v,i),add(v,u,i);
}
}
k=read();
for(int i=1;i<=k;i++) a[i]=read(),nxt[a[i]].push_back(i);
priority_queue<pii,vector<pii>,greater<pii> >q;
for(int i=1;i<=n;i++) dis[i]=inf;
dis[1]=0,q.push(pii(0,1));
while(!q.empty())
{
int u=q.top().se,f=q.top().fi; q.pop();
if(dis[u]!=f) continue;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to,id=e[i].id;
int w=get(dis[u],id);
if(dis[v]>w) dis[v]=w,q.push(pii(dis[v],v));
}
}
if(dis[n]==inf) printf("-1\n");
else printf("%d\n",dis[n]);
return 0;
}
C. Minimum Array
被 A2 卡没时间了 /oh
Description
给一个长度为 \(n\) 的初始序列 \(a\) 和 \(q\) 次操作。每次操作形如给 \(a_l\sim a_r\) 的值加上 \(k\)。
依次进行这些操作,求过程中得到过字典序最小的序列。
$n,q\le 5\times 10^5,\ - 10^9\le a_i,k\le 10^9 $。
Solution 1
考虑依次进行每个操作,维护当前能使答案字典序最小的操作编号 \(ans\)。
只考虑从上一个 \(ans\) 到当前时刻的操作,设它们操作后形成的序列为 \(b\)。那么当前的实际序列就是 \([1,ans]\) 的实际序列与 \(b\) 数组对应位相加后的结果。
当前序列比 \([1,ans]\) 字典序更小的充要条件是 \(b\) 中第一个不为 \(0\) 的位置的值 \(<0\),证明是显然的。每次修改后判断,满足这个条件就更新 \(ans\),并清零 \(b\) 数组。
也就是说我们只需要一个数据结构支持区间加、求第一个不为 \(0\) 的位置、单点求值。
直接上线段树是可做的。不过发现第一个不为 \(0\) 的位置只能是某个 \(l_i\) 或 \(r_i+1\),所以把这些点塞进 set 里暴力判断即可,区间加用树状数组维护。
Solution 2
看了下官方题解。
我们直接在差分数组上考虑这个问题,修改变成了单点,更新答案还是求第一个不为 \(0\) 的位置。这样就不用写树状数组了。
Code
#define int long long
const int N=5e5+5,inf=1e9;
int t,n,a[N];
struct node{int l,r,k;} q[N];
struct BIT
{
int tr[N];
il void modify(int x,int k) {for(;x<=n;x+=x&(-x)) tr[x]+=k;}
il void add(int l,int r,int k) {modify(l,k),modify(r+1,-k);}
il int query(int x) {int res=0;for(;x;x-=x&(-x)) res+=tr[x];return res;}
}tr;
int ans;
signed main()
{
int T=read();
while(T--)
{
n=read(); ans=0;
for(int i=1;i<=n;i++) a[i]=read(),tr.tr[i]=0;
t=read(); set<int> st;
for(int i=1;i<=t;i++) q[i].l=read(),q[i].r=read(),q[i].k=read();
for(int i=1;i<=t;i++)
{
tr.add(q[i].l,q[i].r,q[i].k);
st.insert(q[i].l),st.insert(q[i].r+1);
while(st.size()&&!tr.query(*st.begin())) st.erase(st.begin());
if(!st.empty()&&tr.query(*st.begin())<0)
{
for(int j=i;j>ans;j--) tr.add(q[j].l,q[j].r,-q[j].k);
ans=i,st.clear();
}
}
for(int i=1;i<=n;i++) tr.tr[i]=0;
for(int i=1;i<=n;i++) tr.modify(i,a[i]-a[i-1]);
for(int i=1;i<=ans;i++) tr.add(q[i].l,q[i].r,q[i].k);
for(int i=1;i<=n;i++) printf("%lld ",tr.query(i));
printf("\n");
}
}
D. Split
Description
定义一个序列是好的,当且仅当它存在某种划分成左右两部分的方案,使左半部分的最大值严格小于右半部分的最小值。
现给出长度为 \(n\) 的序列 \(a\),保证 \(a\) 是一个 \(1\sim n\) 的排列。
\(q\) 次询问,每次询问 \(a\) 的子区间 \([l,r]\) 是否为好的序列。
\(n,q\le 3\times 10^5\)。
Solution
考虑对于一个确定的序列怎么搞。我们枚举一个值域分界点 \(i\),把 \(\le i\) 的分在一边,\(>i\) 的分在另一边,判断它们是否恰好是原序列的某种划分。
然而这个东西没有单调性,从其它角度优化这个过程。
我们对于每个下标 \(i\),不考虑具体的询问,而是考虑能使 \(a_i\) 成为合法的值域分界点的区间 \([l,r]\) 中 \(l,r\) 的范围。
首先,\(a_i\) 一定在左半部分,且是左半部分的最大值。那么令 \(x\) 为 \(i\) 向左找第一个 \(a_x>a_i\) 的位置。则左端点有限制 \(x< l\le i\)。
右半部分需满足全部值大于 \(a_i\)。那么令 \(y\) 为 \(i\) 右侧第一个 \(a_y>a_i\) 的位置,有限制 \(r\ge y\)。同时令 \(z\) 为 \(y\) 右侧第一个 \(a_z<a_i\) 的位置,有限制 \(y\le r < z\)。
把询问 \([l,r]\) 看作点的坐标,这是一个矩阵加单点查询问题,使用树状数组 + 扫描线维护。
Code
const int N=3e5+5;
int n,m,a[N],pos[N],ans[N],tot;
struct node {int tp,l,r,x,k,y,id;}q[N<<2];
set<int> ls,rs;
il bool cmp(node x,node y)
{
if(x.x!=y.x) return x.x<y.x;
else return x.tp<y.tp;
}
struct BIT
{
int tr[N];
il void modify(int x,int k) {for(;x<=n;x+=x&(-x)) tr[x]+=k;}
il void add(int l,int r,int k) {modify(l,k),modify(r+1,-k);}
il int query(int x) {int res=0;for(;x;x-=x&(-x)) res+=tr[x];return res;}
}tr;
int main()
{
n=read();
for(int i=1;i<=n;i++) a[i]=read(),pos[a[i]]=i,rs.insert(i);
for(int I=1;I<=n;I++)
{
int i=pos[I];
rs.erase(i);
auto itx=rs.lower_bound(i),ity=rs.upper_bound(i);
int x=(itx==rs.begin()||itx==rs.end())?0:*prev(itx);
int y=(ity==rs.end())?n+1:*ity;
auto itz=ls.upper_bound(y);
int z=(itz==ls.end())?n+1:*itz;
q[++tot]={1,x+1,i,y,1,0,0};
q[++tot]={1,x+1,i,z,-1,0,0};
ls.insert(i);
}
m=read();
for(int i=1;i<=m;i++)
{
int l=read(),r=read();
q[++tot]={2,0,0,r,0,l,i};
}
sort(q+1,q+tot+1,cmp);
for(int i=1;i<=tot;i++)
{
if(q[i].tp==1) tr.add(q[i].l,q[i].r,q[i].k);
else ans[q[i].id]=tr.query(q[i].y);
}
for(int i=1;i<=m;i++) printf(ans[i]?"Yes\n":"No\n");
return 0;
}
E. Good Colorings
Description
Alice 和你玩游戏。有一个 \(n\times n\) 的网格,初始时没有颜色。Alice 在游戏开始前依次给其中 \(2n\) 个格子分别涂上了第 \(1\sim 2n\) 种颜色,并告诉你每个颜色的位置。
接下来的每次操作,你可以选择一个未涂色的格子,由 Alice 在 \(2n\) 种颜色中选择一个涂在该格子上,并告诉你该颜色。
如果在某次操作后方格图上存在四个不同颜色的点,且它们的位置形成一个平行于边线的矩形,则输出它们以获得胜利。
你至多进行 \(10\) 次操作,请构造一个获胜方案。交互库自适应,也就是说 Alice 的决策与你的选择有关。
\(T\le200,n\le 1000\)。
Solution
我们把网格图的行列分别看作点,把格子 \((x,y)\) 涂成颜色 \(c\),看作行 \(x\) 向列 \(y\) 连一条边权为 \(c\) 的边。
那么这是一个左右各有 \(n\) 个点的二分图,我们要找的合法矩形就是长度为 \(4\) 且边权互不相同的环。
由于共有 \(2n\) 个点,已经连了 \(2n\) 条不相同的边,则已经连的边一定至少形成一个长度为偶数的环。考虑通过这个环构造答案。
设环上的点分别为 \(a_1,a_2,\dots,a_{2k}\)。每次我们考虑把这个环连一条边对半拆开:
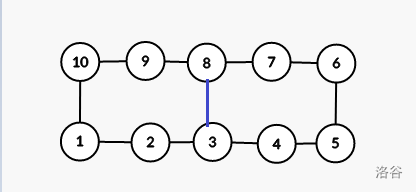
因为整个环上边的颜色都不相同,所以不论新连的边是什么颜色,左右两个环都至少有一个满足环上边的颜色互不相同。选择满足该条件的一侧,重复上述操作,最终一定会得到一个大小为 \(4\) 的环。
由于每次令环长变为原来的一半,至多操作 \(O(\log 2n)-2\) 次。
Code
const int N=2005;
int T,n,f[N][N];
vector<int> e[N],a,b;
stack<int> q;
int in[N],flag,vis[N];
void dfs(int u,int lst)
{
// cerr<<u<<" "<<lst<<" "<<q.size()<<endl;
if(flag) return;
vis[u]=1,in[u]=1,q.push(u);
for(auto v:e[u]) if(v^lst)
{
if(flag) return;
if(in[v])
{
// cerr<<"v "<<v<<" "<<u<<" "<<q.size()<<endl;
assert(q.size());
while(q.top()!=v) a.push_back(q.top()),q.pop();
a.push_back(v),flag=1;return;
}
dfs(v,u);
}
in[u]=0;if(!q.empty()) q.pop();
}
il void clear()
{
// cerr<<"qwq"<<n<<endl;
a.clear(); flag=0;
// cerr<<"?"<<" "<<q.size()<<endl;
while(!q.empty()) q.pop();
// cerr<<"?"<<endl;
for(int i=1;i<=(n<<1);i++)
{
// cerr<<i<<endl;
vis[i]=0,in[i]=0;
for(auto v:e[i]) f[i][v]=0;
e[i].clear();
}
}
il int ask(int x,int y)
{
if(x>y) swap(x,y);
cout<<"? "<<x<<" "<<y-n<<endl;
return read();
}
il void solve()
{
n=read();
for(int i=1;i<=(n<<1);i++)
{
int u=read(),v=read();
e[u].push_back(v+n),e[v+n].push_back(u),f[u][v+n]=f[v+n][u]=i;
}
for(int i=1;i<=n;i++) if(!vis[i]) dfs(i,0);
while(a.size()>4)
{
int sz=a.size()-1,mid=sz/4;
assert(sz&1); int x=a[sz-mid],y=a[mid];
int col=ask(x,y),fg=1;
f[x][y]=f[y][x]=col,e[x].push_back(y),e[y].push_back(x);
for(int i=mid;i<sz-mid;i++) if(f[a[i]][a[i+1]]==col) fg=0;
b.clear();
if(fg) for(int i=mid;i<=sz-mid;i++) b.push_back(a[i]);
else {for(int i=0;i<=mid;i++) b.push_back(a[i]);for(int i=sz-mid;i<=sz;i++) b.push_back(a[i]);}
swap(a,b);
}
assert(a.size()==4);
sort(a.begin(),a.end());
cout<<"! "<<a[0]<<" "<<a[1]<<" "<<a[2]-n<<" "<<a[3]-n<<endl;
string s;cin>>s;
if(s=="ERROR") exit(0);
}
int main()
{
T=read();
while(T--) solve(),clear();
return 0;
}
F. Minimum Segments
不会。
本文来自博客园,作者:樱雪喵,转载请注明原文链接:https://www.cnblogs.com/ying-xue/p/cf1887.html


