Burnside 引理 与 Pólya 定理 学习笔记

为了防止明天就把好不容易听完的东西都还给 rabbit_lb 了，还是记一点吧。

1. 群论基础

1.1 群(group) 的定义

给定集合 \(G\) 和 \(G\)上的二元运算 \(\cdot\)，满足下列条件称之为群：

• 封闭性：若 \(a,b\in G\)，则 \(a\cdot b\in G\)。
• 结合律：对于任意 \(a,b,c\in G\)，有 \((a\cdot b)\cdot c=a\cdot (b\cdot c)\)。
• 单位元：存在单位元 \(e\in G\)，\(\forall a\in G,\, a\cdot e=e\cdot a=a\)。
• 逆元：对于任意 \(a\in G\)，存在 \(b\in G\)，使得 \(a\cdot b=b\cdot a=e\)。记为 \(b=a^{-1}\)。

1.2 一些概念

• 群元素个数有限则称为有限群，无限则称为无限群。

• 有限群 \(G\) 的元素个数叫做群的阶，记做 \(|G|\)。

• 设 \(G\) 和 \(G\)上的二元运算 \(\cdot\) 构成一个群，\(H\) 是 \(G\) 的子集，且 \(H\) 在原有运算下也是一个群，则 \(H\) 为 \(G\) 的一个子群。

• 若群 \(G\) 的任意两元素均满足交换律，则称 \(G\) 为交换群（Abel 群）。

1.3 群的性质

• 单位元唯一：\(e_1e_2=e_1=e_2\)
• 消去律：\(ab=ac\Rightarrow b=c\)
• 每个元的逆元唯一：反证，若 \(aa^{-1}=a^{-1}a=e,\, ab^{-1}=a^{-1}b=e\)，则 \(aa^{-1}=ab^{-1}\)，即 \(a^{-1}=b\)。
• 若 \(G\) 有限，且 \(a\in G\)，则存在最小正整数 \(r\)，使得 \(a^r=e\)，且 \(a^{-1}=a^{r-1}\)。\(r\) 称为 \(a\) 的阶。

2. 置换群

2.1 置换

\([1,n]\) 到自身的一个映射称为 \(n\) 阶置换，表示为 \(\begin{pmatrix}1&2&\dots & n\\a_1&a_2&\dots&a_n\end{pmatrix}\)，其中 \(a_1,a_2,\dots,a_n\) 是 \([1,n]\) 的一个排列。

\(n\) 阶置换共有 \(n!\) 个，同一个置换有 \(n!\) 中表示方法，如 \(p_1=\begin{pmatrix}1&2&3&4\\3&1&2&4\end{pmatrix}=\begin{pmatrix}3&1&4&2\\2&3&4&1\end{pmatrix}\)。\(n\) 阶置换也可以看作 \([1,n]\) 上的一元运算。

设 \(P_1=\begin{pmatrix}1&2&\dots & n\\a_1&a_2&\dots&a_n\end{pmatrix},\, P_2=\begin{pmatrix}1&2&\dots & n\\b_1&b_2&\dots&b_n\end{pmatrix}\)，则定义置换乘法 \(P_1P_2=\begin{pmatrix}1&2&\dots & n\\b_{a_1}&b_{a_2}&\dots&b_{a_n}\end{pmatrix}\)。

置换乘法不满足交换律，但满足结合律。

2.2 置换群

\([1,n]\) 上由多个置换组成的集合，在 2.1 的乘法定义下构成的群，称为置换群。

• 封闭性：\(\begin{pmatrix}1&2&\dots & n\\a_1&a_2&\dots&a_n\end{pmatrix} \begin{pmatrix}a_1&a_2&\dots & a_n\\b_1&b_2&\dots&b_n\end{pmatrix}=\begin{pmatrix}1&2&\dots & n\\b_1&b_2&\dots&b_n\end{pmatrix}\)
• 结合律：由 2.1 知置换乘法满足结合律。
• 单位元：\(e=\begin{pmatrix}1&2&\dots & n\\1&2&\dots&n\end{pmatrix}\)
• 逆元：\(\begin{pmatrix}1&2&\dots & n\\a_1&a_2&\dots&a_n\end{pmatrix}^{-1}=\begin{pmatrix}a_1&a_2&\dots & a_n\\1&2&\dots&n\end{pmatrix}\)

\([1,n]\) 上的所有（\(n!\) 个）置换构成的群，称为 \(n\) 阶对称群，记作 \(S_n\)。平时所说的 \([1,n]\) 上的一个置换群，一定是 \(S_n\)的子群。

2.3 循环

2.3.1 置换的循环表示

置换 \(\begin{pmatrix}1&2&\dots & n\\a_1&a_2&\dots&a_n\end{pmatrix}\) 可以写作 \((1,a_1,a_{a_1},\dots)(\dots)\) 的形式，称为置换的循环表示。E.g. \(\begin{pmatrix}1&2&3 & 4&5\\3&1&2&5&4\end{pmatrix}=(132)(45)\)，\(\begin{pmatrix}1&2&3 & 4&5\\5&2&3&1&4\end{pmatrix}=(154)(2)(3)\)。

\((a_1a_2\dots a_m)\) 称为 \(m\) 阶循环，有 \(m\) 种表示方法。

通常情况下，我们可以忽略所有阶为 \(1\) 的循环。两个不相交的循环之间满足交换律。

定理：任意置换可表示成若干不相交循环的积。

证明：考虑令置换 \(i\) 向 \(a_i\) 连边，图由若干个环构成。显然每个环都可以表示成一个循环。

2.3.2 共轭类

我们设置换 \(p\) 的循环表示为 $p=(a_1a_2\dots a_{k_1})(b_1,b_2\dots b_{k_2})\dots (h_1h_2\dots h_{k_n})，其中 $$\sum\limits_{i=1}^n k_i=n$。设 \(k\) 阶循环出现的次数为 \(c_k\)。
那么置换 \(p\) 的格式为 \((1)^{c_1}(2)^{c_2}\dots(n)^{c_n}\)。E.g. \((1)(23)(4567)\) 的格式为 \((1)^1(2)^1(4)^1\)。

则 \(S_n\) 中所有相同格式的置换构成一个共轭类。

定理：\(S_n\) 中 \((1)^{c_1}(2)^{c_2}\dots(n)^{c_n}\) 所在的共轭类元素个数为 \(\dfrac{n!}{(c_1!c_2!\dotsc_n!)(1^{c_1}2^{c_2}\dots n^{c_n})}\)。

可以这样理解这个式子：

• 一个长度为 \(i\) 的循环共有 \(i\) 种表示，\(c_i\) 个长度为 \(i\) 的循环有 \(i^{c_i}\) 种表示；
• 对互不相交的 \(c_i\) 个循环枚举全排列，共有 \(c_i!\) 种表示。

2.3.3 对换与奇偶置换

\(2\) 阶循环叫做对换。

定理：任意循环都可以表示为若干对换的积。

推柿子：

\[\begin{aligned} &(1\, 2\, 3\dots n-1)(1\, n)\\ =&\begin{pmatrix}1&2&\dots & n-1\\2&3&\dots&1\end{pmatrix}\begin{pmatrix}1&2&\dots & n-1&n\\n&2&\dots&n-1&1\end{pmatrix}\\ =&\begin{pmatrix}1&2&\dots & n-1&n\\2&3&\dots&n&1\end{pmatrix}\\ =&(1\,2\,\dots\,n) \end{aligned} \]

那么进一步地，有分解 \((1 2\dots n)=(12)(13)\dots(1n)\)。注意每个置换的分解不唯一。

若一个置换能分解为奇数个对换之积，则为奇置换；否则为偶置换。

Warning. 置换相乘的奇偶性类似于自然数加法，而非自然数乘法：奇 x 奇 = 偶，奇 x 偶 = 奇。

3. Burnside 引理

3.1 等价类与 \(k\) 不动置换类

设 \(G\) 是 \([1,n]\) 上的一个置换群，\(k\in [1,n]\)。\(G\) 中使 \(k\) 元素保持不变的置换全体，称为 \(k\) 不动置换类，记作 \(Z_k\)。

定理：置换群 \(G\) 的 \(k\) 不动置换类 \(Z_k\) 是 \(G\) 的子群。

• 封闭性：\(k\) 怎么置换都不动。
• 结合性：显然。
• 单位元：\(G\) 的单位元也在 \(Z_k\) 中。
• 逆元：\(Z_k\) 中的置换 \(p\) 在 \(G\) 中的逆元 \(p^{-1}\) 也在 \(Z_k\) 中。

置换 \(p_i\) 使图像 \(k\) 变为 \(l\)，则称 \(k\) 和 \(l\) 属于同一个等价类。设 \(k\) 所在的等价类记为 \(E_k\)。

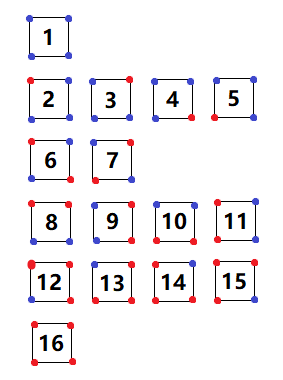
如图，将正方形四个顶点红蓝染色，等价类个数为 \(6\)。（每行是一个等价类）

3.2 轨道稳定子定理

定理：设 \(G\) 是 \([1,n]\) 上的一个 置换群，\(E_k\) 是 \([1,n]\) 在 \(G\) 的作用下包含 \(k\) 的等价类，\(Z_k\) 是 \(k\)不动置换类。有 \(|E_k||Z_k |=|G|\)。

证明：每个等价类有 \(|E_k|\) 个元素，同时因为它们属于同一等价类，每个元素的 \(Z_k\) 相同。因此这些 \(Z_k\) 覆盖了整个 \(G\)，即每个等价类都有 \(|E_k||Z_k |=|G|\)。

3.3 Burnside 引理

将上式变形，有：

\[\sum_{k=1}^n \frac{|Z_k|}{|G|}=\sum_{k=1}^n \frac{1}{|E_k|} \]

仔细想一下会发现 \(\sum_{k=1}^n \frac{1}{|E_k|}\) 就是等价类个数。

然而问题并没有解决，因为 \(Z_k\) 不好求。进一步地，我们定义 \(c_1(a_k)\) 表示在置换 \(a_k\) 的作用下不动点的个数，即长度为 \(1\) 的循环个数。那么等价类个数为：

\[l=\frac{1}{|G|}\sum_{j-1}^n c_1(a_j) \]

这个式子就是 Burnside 引理。

4. Pólya 定理

Pólya 定理是 Burnside 引理的推广，应用于 染色问题 的 循环同构 方案计数。

设 \(G=\{P_1,P_2,\dots,P_g\}\) 是 \(n\) 个对象 的一个置换群，\(C(P_k)\) 是置换 \(P_k\) 的循环的个数，用 \(m\) 种颜色对 \(n\) 个对象着色，着色方案数为

\[l=\frac{1}{|G|} \sum_{j=1}^g m^{C(P_j)} \]

接下来用一个例题说明该定理的具体用法。

用火柴搭一个足球，有多少种方案？

Tips: 足球有 \(60\) 个顶点，\(90\) 条棱，\(12\) 个五边形，\(20\) 个六边形。

• 不动：\(1\) 种置换，\(2^{90}\) 种染色；
• 五边形对五边形转：\(6\times 4=24\) 种置换，\(2^{90/5}\) 种染色；
• 六边形对六边形转：\(10\times 2=20\) 种置换，\(2^{90/3}\) 种染色；
• 棱中点对棱中点转：\(15\) 种置换，\(0\) 种染色（一定都会变）。

则本质不同的方案数为 \((2^{90}+24\times 2^{18}+20\times 2^{30})/(1+24+20+15)\)。

5. 例题

P4980【模板】Polya 定理

板子。发现置换只有旋转，考虑枚举旋转的角度，有：

\[\frac{1}{n}\sum_{k=1}^n n^{\gcd(k,n)} \]

枚举 \(\gcd\)，可以变成

\[\frac{1}{n} \sum_{d\mid n}n^d \sum_{k=1}^{\frac{n}{d}}[\gcd(k,\frac{n}{d})=1] \]

也就是

\[\frac{1}{n}\sum_{d\mid n}n^d\varphi(\frac{n}{d}) \]

暴力计算欧拉函数即可通过。

Code

#define int long long 
const int mod=1e9+7;
int T,n;
il int qpow(int n,int k=mod-2)
{
    int res=1; 
    for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
    return res;
}
il int phi(int x)
{
    int res=x;
    for(int i=2;i*i<=x;i++)
    {
        if(x%i==0) res=res/i*(i-1);
        while(x%i==0) x/=i;
    }
    if(x>1) res=res/x*(x-1);
    return res;
}
signed main()
{
    T=read();
    while(T--)
    {
        n=read(); 
        int ans=0;
        for(int d=1;d*d<=n;d++) if(n%d==0)
        {
            (ans+=qpow(n,d)*phi(n/d)%mod)%=mod;
            if(d*d!=n) (ans+=qpow(n,n/d)*phi(d)%mod)%=mod;
        }
        ans=ans*qpow(n)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

CF1065E Side Transmutations

首先可以发现翻转是可以抵消的。如果我们操作 \(b_1\)，再操作 \(b_2\)，再操作 \(b_1\)，这相当于只操作了一个 \(b_2\)。也就是说，想要得到最终状态我们只关心每个 \(b_i\) 被操作次数的奇偶性。

考虑 Polya 定理，但是发现不动点看起来不好算。

进一步对 \(b_i\) 进行转化，考虑将字符串分成形如 \([b_1,b_2),[b_2,b_3),\dots\) 的若干段。那么我们统计不动点的时候只关心每一段是否被翻转。
不难看出，字符串每段的翻转状态与 \(b\) 的操作次数奇偶性序列构成双射。设 \(len_i\) 表示第 \(i\) 段的长度。

那么如果第 \(i\) 段被翻转了，这一段本身的贡献是 \(|A|^{len_i}\)；否则为 \(|A|^{2len_i}\)。而对于中间长度为 \(n-2len_m\) 且永远不会被翻转的段，贡献恒为 \(|A|^{n-2len_m}\)。

故设 \(T=\{1,2,\dots,n\}\)，本质不同的方案数为

\[\begin{aligned} &\frac{|A|^{n-2len_m}}{2^m}\sum_{S\sube T}([i\in S]|A|^{len_i})+([i\notin S]|A|^{2len_i})\\ =&\frac{|A|^{n-2len_m}}{2^m}\prod_{i=1}^m (|A|^{len_i}+|A|^{2len_i}) \end{aligned} \]

直接计算即可，时间复杂度为 \(\mathcal{O}(m\log n)\)。

Code

#define int long long
const int N=2e5+5,mod=998244353;
int n,m,A,b[N];
int l[N];
il int qpow(int n,int k=mod-2)
{
    int res=1;
    for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
    return res;
}
signed main()
{
    n=read(),m=read(),A=read();
    for(int i=1;i<=m;i++) b[i]=read();
    for(int i=1;i<=m;i++) l[i]=b[i]-b[i-1];
    int sum=1,ans=0;
    for(int i=1;i<=m;i++) sum=sum*(qpow(A,l[i])+qpow(A,2*l[i]))%mod;
    ans=sum*qpow(A,n-2*b[m])%mod;
    ans=ans*qpow(qpow(2,m))%mod;
    printf("%lld\n",ans);
    return 0;
}

ARC062F Painting Graphs with AtCoDeer

一个比较直观的性质是，一条边无论如何都转不出自己所在的边双连通分量。进一步地，发现实际上一条边转不出自己所在的点双。这似乎有点反直觉，但考虑下图，边无法从一个环移到另一个环：

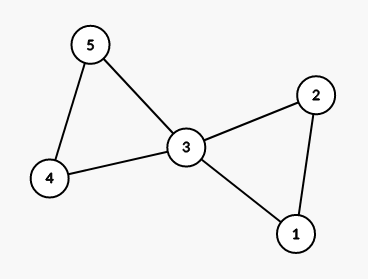
那么根据这个结论，每个点双之间是独立的。分类讨论：

• 如果一条边的两个端点不在同一点双里，这条边对答案的贡献是 \(k\)；
• 如果点双是一个环，这是 Polya 定理的板子；
• 否则有结论：如果一个点双有至少两个环，所有边都可以任意交换。

考虑证明上述结论，我们只需证明存在一种方案，在不改变其他边的情况下交换两条边。

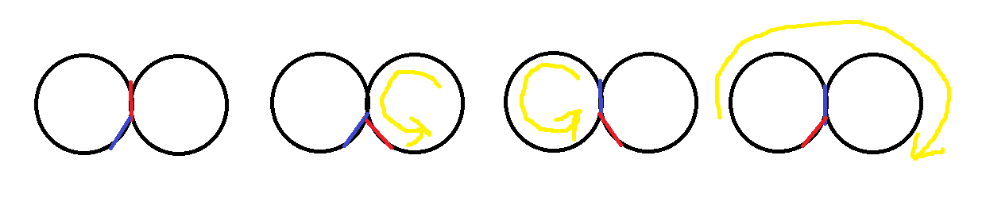
使用上图的做法可以交换两环交界处的两条边。对于不在两环交界处的边，可以先转到交界处再如此操作。
故设这个点双有 \(cnt\) 条边，对答案的贡献就是 \(cnt\) 条边涂 \(k\) 个颜色，不区分顺序的方案数。经典插板法，为 \(\binom{cnt+k-1}{k-1}\)。

对以上三种情况分别计算贡献即可。

Code

#define int long long
const int N=205,mod=1e9+7;
int n,m,k;
vector<int> e[N];
int dfn[N],low[N],tot,num;
vector<int> t[N],q;
void tarjan(int u,int fa)
{
    dfn[u]=low[u]=++tot; q.push_back(u);
    for(auto v:e[u]) if(v^fa)
    {
        if(!dfn[v])
        {
            tarjan(v,u),low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                num++;
                while(q.back()!=u) 
                {
                    int x=q.back();
                    t[num].push_back(x),q.pop_back();
                    if(x==v) break;
                }
                t[num].push_back(u);
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
}
int bel[N];
il int qpow(int n,int k=mod-2)
{
    int res=1;
    for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
    return res;
}
il int solve(int m)
{
    int res=0;
    for(int i=1;i<=m;i++) res=(res+qpow(k,__gcd(i,m)))%mod;
    res=res*qpow(m)%mod; return res;
} 
int jc[N],inv[N];
il void init(int mx)
{
    jc[0]=inv[0]=1;
    for(int i=1;i<=mx;i++) jc[i]=jc[i-1]*i%mod;
    inv[mx]=qpow(jc[mx]);
    for(int i=mx-1;i;i--) inv[i]=inv[i+1]*(i+1)%mod;
}
il int C(int n,int m) 
{
    if(m>n) return 0;
    return jc[n]*inv[n-m]%mod*inv[m]%mod;
}
signed main()
{
    n=read(),m=read(),k=read();
    for(int i=1;i<=m;i++)
    {
        int u=read(),v=read();
        e[u].push_back(v),e[v].push_back(u);
    }
    init(m+k);
    int ans=1;
    for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0);
    for(int i=1;i<=num;i++)
    {
        for(auto x:t[i]) bel[x]=i;
        int cnt=0;
        for(auto u:t[i])
            for(auto v:e[u]) if(bel[v]==i) cnt++;
        cnt>>=1;
        m-=cnt;
        if(cnt>t[i].size()) ans=ans*C(cnt+k-1,k-1)%mod;
        else if(cnt==t[i].size()) ans=ans*solve(cnt)%mod;
        else ans=ans*qpow(k,cnt)%mod;
    }
    printf("%lld\n",ans);
    return 0;
}

[HNOI2009] 图的同构计数

我们可以把每条边选与不选看作对一个完全图上的边黑白染色，这与原题意是等价的。

使用 Polya 定理，先枚举一个置换，并把置换写成循环的形式。考虑对在该置换下不变的染色方案进行计数。

根据一条边的两个端点是否在同一个循环内，分类讨论：

• 如图，若一条边的两个端点属于同一循环，那么它应当与循环内所有长度相等的边同色。
  
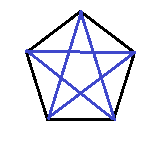
  那么一个长度为 \(len\) 的循环，其内部共有 \(\lfloor \frac{len}{2}\rfloor\) 类等价的边。
• 否则，若一条边连接了两个不同循环，设它们的长度分别为 \(len_i,len_j\)。那么一条边需要做 \(\text{lcm}(len_i,len_j)\) 次置换才能回到它原来的位置，即等价类个数为 \(\gcd(len_i,len_j)\)。

综上，一个 \(len\) 序列对 polya 求和式子的贡献为

\[S=\sum_{i=1}^n(\lfloor \frac{len_i}{2}\rfloor +\sum_{j=1}^{i-1} \gcd(len_i,len_j)) \]

发现这只与 \(len\) 数组有关而与具体的置换无关，考虑只枚举 \(len\) 数组，并计算有多少种对应的置换。由 2.3.2 可知，设 \(c_i\) 表示 \(len_j=i\) 的 \(j\) 的个数，对应的置换数为

\[\frac{n!}{\prod len_i\prod (c_i!)} \]

总答案为

\[\frac{1}{n!}\sum_{len}\frac{n!}{\prod len_i\prod (c_i!)} 2^S \]

其中 \(S\) 见上文。时间复杂度为 \(n\) 的无序拆分数。

Code

#define int long long
const int N=205,mod=997;
int n,ans,tot,b[N],c[N];
il int qpow(int n,int k=mod-2)
{
    int res=1;
    for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
    return res;
}
il int solve()
{
    int res=0;
    for(int i=1;i<=tot;i++)
    {
        res=(res+(b[i]>>1));
        for(int j=1;j<i;j++) res=(res+__gcd(b[i],b[j]));
    }
    return res;
}
void dfs(int sum)
{
    if(!sum)
    {
        int k=solve();
        int v=1;
        for(int i=1;i<=n;i++) c[i]=0;
        for(int i=1;i<=tot;i++) v=v*b[i]%mod,c[b[i]]++;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=c[i];j++) v=v*j%mod;
        ans=(ans+qpow(2,k)*qpow(v)%mod)%mod;
        return;
    }
    for(int k=b[tot];k<=sum;k++)
    {
        b[++tot]=k,dfs(sum-k);
        tot--;
    }
}
signed main()
{
    n=read();
    b[0]=1; dfs(n);
    printf("%lld\n",ans);
    return 0;
}

P4128 [SHOI2006] 有色图

与上题同理，将 \(2\) 换为 \(k\) 即可。