AGC 020~025 记录
AGC020
D. Min Max Repetition
Tags: binary search.
要令连续的相同字符个数的最大值最小，可以直接贪心将 A 和 B 尽可能分开，得出答案 \(k=\lfloor\frac{A+B}{\min(A,B)+1}\rfloor\)。
接下来要在这个基础上构造字典序最小的答案。
我们显然希望 A 尽量靠前，直到超出限制时再用 B 分开，即靠前部分的答案形如 AAABAAABAAAB...。但是后面大量的 B 还需要用 A 分开，我们希望尽量少的 A 被放在后面，则后面部分的答案形如 BBBABBBABBB...。
也就是说，完整的答案字符串由前后两部分拼成，前半部分每放 \(k\) 个 A 放 \(1\) 个 B；后半部分每放 \(k\) 个 B 放 \(1\) 个 A。
那么我们可以二分这个位置 \(p\)，\(\text{check}\) 时分别求出前后所需的两种字符个数即可。
注意 \(\text{check}\) 的时候别爆 int。
Code
#define int long long
int T,A,B,C,D,k;
il bool check(int x)
{
int cntb=x/(k+1),cnta=cntb*k+x%(k+1);
return (B-cntb)<k*(A-cnta+1);
}
signed main()
{
T=read();
while(T--)
{
A=read(),B=read(),C=read(),D=read();
k=max((A+B)/(B+1),(A+B)/(A+1));
int l=0,r=A+B;
while(l<r)
{
int mid=(l+r+1)>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
for(int i=C;i<=D;i++)
{
if(i<=l) printf(i%(k+1)==0?"B":"A");
else printf((A+B-i+1)%(k+1)==0?"A":"B");
}
printf("\n");
}
return 0;
}
E. Encoding Subsets
Tags: dp，记搜
没发现状态数很少的性质。
考虑区间 dp，设 \(f_{l,r}\) 表示 \([l,r]\) 这段子串压缩成任意段的方案数，\(g_{l,r}\) 表示只压缩成一段的方案数。这样设状态避免了重复计数。
那么有：
注意到，即使 \(l,r\) 不同，但区间内的字符串可能是一样的，这样的重复状态无需重复计算。因此我们把 \([l,r]\) 所代表的字符串直接压进状态，记搜转移即可。实际有效的状态数不多，可以通过。
Code
#include<bits/stdc++.h>
#define il inline
using namespace std;
il long long read()
{
long long xr=0,F=1; char cr;
while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
while(cr>='0'&&cr<='9')
xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
return xr*F;
}
#define int long long
const int N=105,mod=998244353;
int n;
string s;
map<string,int> f,g;
int F(string s);
int G(string s)
{
if(g.count(s)) return g[s];
if(s=="0") return 1; else if(s=="1") return 2;
int res=0;
for(int d=1;d<s.size();d++)
{
if(s.size()%d) continue;
string t;
for(int i=0;i<d;i++)
{
bool flag=1;
for(int j=i;j<s.size();j+=d) if(s[j]!='1') flag=0;
t+=flag+'0';
}
res=(res+F(t))%mod;
}
return g[s]=res;
}
int F(string s)
{
if(f.count(s)) return f[s];
int res=G(s);
for(int i=1;i<s.size();i++)
{
(res+=G(s.substr(0,i))*F(s.substr(i,s.size()-i+1))%mod)%=mod;
}
return f[s]=res;
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>s;
printf("%lld\n",F(s));
return 0;
}
F. Arcs on a Circle
Tags: 状压，离散化，期望
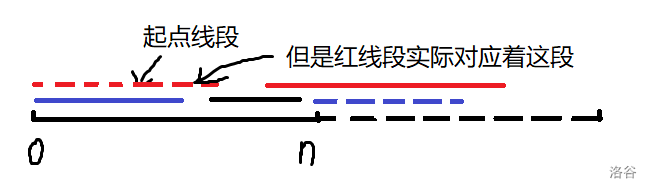
先断环为链，并以最长线段的起点作为整条链的起点。那么我们只需要让这条链上 \([0,n)\) 的位置都被覆盖就行了。
如果没有选最长线段做起点，可能出现一条线段把起点线段覆盖住的情况，这样也是合法的，但并没有按上述条件覆盖 \([0,n)\) 的位置。下图是一个例子。
然后这个问题的瓶颈在于坐标可以是实数。
但因为长度都是整数，我们只需要知道两条线段起点的整数部分和小数部分的相对大小关系就可以判断它们是否相交。
这启发我们枚举每条线段之间小数部分的大小关系，并将其离散化。那么我们拥有了 \(nc\) 个整数坐标，线段只能分布在其小数部分对应的整数坐标上。
这样就可以把坐标塞进 dp 状态了：设 \(f_{i,j,s}\) 表示考虑了左端点坐标不超过 \(i\) 的线段，覆盖了 \([0,j]\) 的所有位置，使用过的线段集合为 \(s\) 的方案数。
因为放线段随机，所以每种小数部分大小关系概率相等，可以计算出对应的期望贡献。
时间复杂度 \(O(n!2^n(nc)^2)\)，不过 \(n\) 只有 \(6\)，能过。
Code
const int N=55;
int n,c,a[N],vis[N],jc[N],tot;
int f[N*6][(1<<6)+5];
double ans;
il double qpow(double n,int k)
{
double res=1;
for(;k;n=n*n,k>>=1) if(k&1) res=res*n;
return res;
}
int main()
{
n=read(),c=read();
for(int i=0;i<n;i++) a[i]=read();
sort(a,a+n);
do
{
tot++;
memset(f,0,sizeof(f));
f[a[n-1]*n][0]=1;
for(int i=1;i<=c*n;i++)
{
if(i%n==0) continue;
for(int j=i;j<=c*n;j++)
{
for(int s=0;s<(1<<n-1);s++)
{
int x=i%n-1;
if(s>>x&1) continue;
f[min(c*n,max(j,i+a[x]*n))][s^(1<<x)]+=f[j][s];
}
}
}
ans+=f[c*n][(1<<n-1)-1];
}while(next_permutation(a,a+n-1));
printf("%.12lf\n",1.0*ans/tot/qpow(c,n-1));
return 0;
}
AGC021
E. Ball Eat Chameleons
为什么做过一次的题还不会做？
首先考虑一个变色龙最后是红色的条件：
- 红球比蓝球多
- 两种球一样多，且最后一次喂的是蓝球
设共有 \(a\) 个红球，\(b\) 个蓝球，根据题意有 \(a+b=k\)。
那么当 \(a\le b+n\) 时，一定存在某种方式使所有变色龙的红球都比蓝球多。所以一定合法。
同理，当 \(a<b\) 时一定不合法。
我们只需要考虑 \(0\le a-b < n\) 的情况。再观察性质：
- 希望红蓝相等的变色龙数尽可能少，因此变色龙只有两种：红蓝相等，红比蓝多 \(1\)。
- 如果一个变色龙红蓝相等，且吃的球数大于 \(2\)，我们可以在不为结尾的位置取出一对红蓝球，把它们改成喂给红球比蓝球多的那只。
- 所以进一步地，变色龙只有两种：恰好被喂一个红球一个蓝球，红球比蓝球多一个。后者有 \(a-b\) 个，前者有 \(n-a+b\) 个。
因此只要能在颜色序列里选出 \(n-a+b\) 对有顺序的红球和蓝球就合法。这等价于不越过 \(y=x+n-a+b\) 的折线数，可以根据卡特兰数的相关推导方法得出答案：
枚举 \(a\) 计算答案即可。
Code
#define int long long
const int N=5e5+5,mod=998244353;
int n,k;
int jc[N],inv[N];
il int qpow(int n,int k=mod-2)
{
int res=1;
for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
return res;
}
int c(int n,int m)
{
if(m>n) return 0;
return jc[n]*inv[m]%mod*inv[n-m]%mod;
}
signed main()
{
n=read(),k=read();
if(n>k) {printf("0\n");return 0;}
jc[0]=inv[0]=1;
for(int i=1;i<=k;i++) jc[i]=jc[i-1]*i%mod;
inv[k]=qpow(jc[k]);
for(int i=k-1;i;i--) inv[i]=inv[i+1]*(i+1)%mod;
int ans=0;
for(int r=(k+1)/2;r<=k;r++)
{
int b=k-r;
if(b==r) b--;
ans=(ans+c(r+b,r)-c(r+b,2*r-n+1)+mod)%mod;
}
printf("%lld\n",ans);
return 0;
}
F. Trinity
Tags: 组合计数，dp，NTT
设 \(f_{i,j}\) 表示一个 \(i\times j\) 的矩阵，每行都有至少一个黑格子的方案数。那么总的方案就是在其中选择一些存在黑格子的行，有
按列填数转移。枚举考虑了前 \(j-1\) 列有 \(k\) 行已经存在黑格子。那么分为两种情况：
- \(k=i\)，则这一列没有新的行变黑，也就是说 \(A\) 数组不变。只需考虑填数对 \(B,C\) 的影响。再分类讨论：
- \(B_j=n+1,C_j=0\)，即这一列什么都不填，方案数为 \(1\)；
- \(B_j=C_j\)，即这一列只填了一个位置，方案数为 \(i\)；
- \(B_j<C_j\)，这一列填了至少两个位置。但我们不关心具体怎么填，只关心 \(B,C\) 序列的值。所以方案数为 \(\binom{i}{2}\)。
转移为
- \(k<i\)，说明有 \(i-k\) 行是在这列变黑的。但这里显然不能简单地乘上 \(\binom{i}{i-k}\)，因为在变黑的行均相同的情况下，原来就为黑色的行的不同填法对 \(B,C\) 数组产生的贡献不一定相同。
所以考虑在对新加的行计数时也同时对这一列的最值计数。继续分类讨论：- 如果两个最值都是新加的行，方案数为 \(\binom{i}{i-k}\)；
- 如果其中一个不是新加的行，这等价于选了 \(i-k+1\) 个位置，然后强制钦定最小的那个是在已经出现过的行。最大值同理，方案数为 \(2\times \binom{i}{i-k+1}\)；
- 如果两个都不是新加的行，等价于选了 \(i-k+2\) 个位置，方案数为 \(\binom{i}{i-k+2}\)。
求和，发现 \(\binom{i}{i-k}+2\times \binom{i}{i-k+1}+\binom{i}{i-k+2}=\binom{i+2}{i-k+2}\)。这种情况的转移是
总转移为
朴素实现是 \(\mathcal{O}(n^2m)\)。注意到瓶颈在式子的后面一半，把组合数拆开：
发现是卷积，赢！NTT 优化一下就变成 \(\mathcal{O}(nm\log n)\) 了。
有人阶乘处理挂了对着 NTT 虚空查错一上午，我不说是谁。
Code
#define int long long
const int N=8e3+5,mod=998244353;
int n,m,a[N<<2],b[N<<2],limit=1,to[N<<2];
il int qpow(int n,int k=mod-2)
{
int res=1;
for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
return res;
}
il void NTT(int *a,int tp)
{
for(int i=0;i<limit;i++) if(i<to[i]) swap(a[i],a[to[i]]);
for(int len=1;len<limit;len<<=1)
{
int Wn=qpow(qpow(3,(mod-1)/(len<<1)),tp);
for(int i=0;i<limit;i+=(len<<1))
for(int j=0,w=1;j<len;j++,w=w*Wn%mod)
{
int x=a[i+j],y=a[i+len+j];
a[i+j]=(x+w*y)%mod,a[i+len+j]=(x-w*y%mod+mod)%mod;
}
}
if(tp^1) for(int i=0;i<limit;i++) a[i]=a[i]*qpow(limit)%mod;
}
int f[N][205],jc[N<<2],inv[N<<2];
void init(int mx)
{
jc[0]=inv[0]=1;
for(int i=1;i<=mx;i++) jc[i]=jc[i-1]*i%mod;
inv[mx]=qpow(jc[mx]);
for(int i=mx-1;i;i--) inv[i]=inv[i+1]*(i+1)%mod;
}
signed main()
{
n=read(),m=read(); init(n+2);
for(int i=0;i<=n;i++) f[i][1]=1;
int k=0; while(limit<=2*n) limit<<=1,k++;
for(int i=0;i<limit;i++) to[i]=(to[i>>1]>>1)|(i&1)<<k-1;
for(int j=2;j<=m;j++)
{
for(int i=0;i<limit;i++) a[i]=b[i]=0;
for(int i=0;i<=n;i++) a[i]=f[i][j-1]*inv[i]%mod,b[i]=inv[i+2];
b[0]=0;
NTT(a,1),NTT(b,1);
for(int i=0;i<limit;i++) a[i]=a[i]*b[i]%mod;
NTT(a,mod-2);
for(int i=0;i<=n;i++) f[i][j]=(jc[i+2]*a[i]%mod+f[i][j-1]*(1+i+i*(i-1)/2)%mod)%mod;
}
int ans=0;
for(int i=0;i<=n;i++)
ans=(ans+f[i][m]*jc[n]%mod*inv[i]%mod*inv[n-i]%mod)%mod;
printf("%lld\n",ans);
return 0;
}
AGC022
D. Shopping
Tags: 神奇贪心
首先发现答案一定是 \(2L\) 的整数倍，所以我们只需要关心火车至少跑几个来回。
\(t_i>2L\) 的情况处理起来很麻烦，但不论怎么走 \(\lfloor \frac{t_i}{2L}\rfloor\) 这部分对答案的贡献都是不变的。因此可以直接在答案里加上这部分贡献，然后令 \(t_i\gets t_i\bmod 2L\)。取模后为 \(0\) 的 \(t_i\) 对答案不会有进一步贡献，要特判掉。
这样处理后每个点坐火车就只有两种情况了：
- 在这个点下车后，火车下次反方向经过这个点时立刻上车；
- 等火车正好走完一个来回再上车。
因为 \(t_i\) 取过模，所以第二种情况一定是可行的。而第一种是否可行取决于点的位置、购物时间和下车时的方向。
设 \(l_i,r_i\) 表示点 \(i\) 如果从左侧 / 右侧下车，能否满足第一种情况，即在火车再次经过前完成购物。这可以由简单的数学知识求出。
考虑先构造一个可行方案，再对其进行调整：我们从点 \(1\) 开始，每次都采取第二种坐车方法前往下一个点，最后从 \(n\) 坐车回到 \(0\)。这样火车一共跑了 \(n+1\) 个来回。
但这样做很亏，因为火车很多时间都在空跑。尝试调整顺序，让一些点变为第一种乘车方案。如果存在一对 \(i<j\)，且 \(r_i=1,l_j=1\)，那我们从 \(i-1\) 上车后先跑到 \(j\)，在车返回时上车跑到 \(i\)，就在路程不变的情况下成功多跑了一个点 \(j\)。
这样的跑法通过同时让两个点变为相反方向的「第一种乘车方案」，使总答案减少了一个来回。我们要最大化这样的匹配数量。
首先 \((l_i,r_i)=(0,1)\) 和 \((l_j,r_j)=(1,0)\) 肯定匹配不到一起（因为 \(x_i\) 一定在右面一半，\(x_j\) 一定在左面一半）。那么匹配策略就是把形如 \((1,1)\) 的点分别和 \((0,1),(1,0)\) 配对（同理，能匹配的必然不冲突），再把剩下的 \((1,1)\) 两两配对。
最后一点大概就是特判 \(n\) 不能配对，但如果 \(l_n=1\) 可以直接顺路回去省掉一个来回。
Code
const int N=3e5+5;
int n,L,x[N],t[N];
int l[N],r[N];
int main()
{
n=read(),L=read();
for(int i=1;i<=n;i++) x[i]=read();
for(int i=1;i<=n;i++) t[i]=read();
int sum=0,ans=n+1;
for(int i=1;i<=n;i++)
{
ans+=t[i]/(L<<1),t[i]%=L<<1;
if(!t[i]) {ans--;continue;}
r[i]=(t[i]<=x[i]*2);
l[i]=(t[i]<=(L-x[i])*2);
}
for(int i=1,now=0;i<n;i++)
if(l[i]&&r[i]) now++,sum++;
else if(l[i]&&now) now--,sum--,ans--;
for(int i=n-1,now=0;i;i--)
if(l[i]&&r[i]) now++;
else if(r[i]&&now) now--,sum--,ans--;
ans-=(sum>>1)+l[n];
printf("%lld\n",1ll*ans*(L<<1));
return 0;
}
E. Median Replace
Tags: 神奇贪心，dp
居然还记得它怎么做，太感动了。
先考虑对于一个给定的串怎么判定答案。
首先我们希望在不损失 \(\texttt{1}\) 的情况下减少 \(\texttt{0}\) 的个数，因此第一步肯定是把 \(\texttt{000}\) 全消掉。下文均默认做完了这步操作。
然后除了 \(\texttt{111}\)（我们不希望消掉这个）以外每种消法都相当于删掉一个 \(\texttt{0}\) 和一个 \(\texttt{1}\)。因此只要这个序列 \(\texttt{1}\) 比 \(\texttt{0}\) 多就合法。
但是这样直接塞进状态里 dp 复杂度是 \(\mathcal{O}(n^2)\) 的。接着找性质：
- 如果一个前缀 \(\texttt{1}\) 比 \(\texttt{0}\) 多 \(3\) 个，那整个串都赢了。证明的话考虑先把这个前缀消成只剩 \(3\) 个 \(\texttt{1}\)，后面的部分显然不会剩下多于 \(2\) 个连续的 \(\texttt{0}\)。
- 如果一个前缀 \(\texttt{0}\) 比 \(\texttt{1}\) 多 \(3\) 个，相当于只多 \(1\) 个，因为能消掉。
因此我们可以改一下判断合法的过程。
维护一个栈。每次考虑当前字符与栈顶的关系：
- 当前加入 \(\texttt{0}\)
- 栈顶已有两个 \(\texttt{0}\)，把它们三个消成一个；
- 否则入栈。
- 当前加入 \(\texttt{1}\)
- 栈顶是 \(\texttt{0}\)，说明这段 \(\texttt{0}\) 不消除肯定形不成三个连续，因此把当前数和栈顶抵消掉；
- 栈顶是 \(\texttt{1}\)，如果栈里已经有两个了就摆，否则加进去。
为什么这么搞是对的呢？因为栈维护的过程优先消后面的 \(\texttt{0}\)，参见前缀至多 \(3\) 个 \(\texttt{1}\) 的证明。
最后栈里 \(\texttt{1}\) 的个数大于等于 \(\texttt{0}\) 的就合法。
于是设 \(f_{i,x,y}\) 表示前 \(i\) 个，栈里有 \(x\) 个 \(\texttt{0}\) 和 \(y\) 个 \(\texttt{1}\)。dp 转移一下就行了。
Code
const int N=3e5+5,mod=1e9+7;
int n,f[N][5][5];
char s[N];
il void add(int &x,int y) {x+=y;if(x>=mod) x-=mod;}
int main()
{
scanf("%s",s+1);
n=strlen(s+1);
f[0][0][0]=1;
for(int i=1;i<=n;i++)
{
if(s[i]!='1')
{
for(int x=0;x<=2;x++)
{
add(f[i][x][1],f[i-1][x][2]);
add(f[i][x][2],f[i-1][x][1]);
add(f[i][x][1],f[i-1][x][0]);
}
}
if(s[i]!='0')
{
for(int x=0;x<=2;x++)
for(int y=0;y<=2;y++) add(f[i][x][y],f[i-1][x][y+1]);
add(f[i][1][0],f[i-1][0][0]);
add(f[i][2][0],f[i-1][1][0]);
add(f[i][2][0],f[i-1][2][0]);
}
}
int ans=0;
for(int x=0;x<=2;x++)
for(int y=0;y<=x;y++) add(ans,f[n][x][y]);
printf("%d\n",ans);
return 0;
}
F. Checkers
不是，为什么这么抽象的题赛时过的人比 D 多啊？？
对着某篇错的题解瞪了一天，真服了。
考虑转化题意。我们令一次 \(A\) 关于 \(B\) 对称的操作对应为在一个图上将点 \(B\) 向点 \(A\) 连一条边。那么由于一个点被对称过就会消失，在图上对应为只有一条出边。一共有 \(n-1\) 条边且连通，所以这是一棵树。根为最后剩下那个节点编号。
由于对称操作形如 \(A\gets 2B-A\)，过程中每个点的坐标一定形如 \(\sum 2^j (-1)^k x^i\)。由于 \(x\) 足够大，我们可以认为 \(x\) 的不同次幂之间的贡献是互不影响的，也就是说只要这个多项式任意一项系数不同，我们就认为它求和的结果不同。
考虑根据这棵树求出最后点所在的位置，设 \(ans_x\) 表示点 \(x\) 对最后总答案产生的贡献。
在实际过程中，我们一定是以从叶子逐步向上的顺序进行操作，一个点只有在所有叶子都操作完的情况下才能被操作。而考虑一次操作对树上每个点贡献的改变，\(fa_x\) 关于 \(x\) 对称即令 \(x\) 所在的连通块 \(ans\) 全部乘 \(2\)，\(fa_x\) 所在的连通块取反。
那么点 \(x\) 在 \(2^j\) 这部分的贡献显然是 \(2^{dep_x}\)，这只与树的形态有关。另一部分取决于 \(x\) 的儿子数量和深度，两个限制是不好求的，我们做这样的转化：只要知道点 \(x\) 的正负性（下文称之为“颜色”）是否与其父亲节点相同，即可还原出整棵树的颜色。而一个点每加一次儿子就取反一次，这就只与 \(fa_{x}\) 的儿子个数和 \(x\) 被连边的顺序有关了。
进一步地，设点 \(x\) 的儿子个数为 \(son_x\)，则恰有 \(\lfloor \frac{son_x}{2}\rfloor\) 个儿子取反偶数次。
性质足够了，考虑 dp。从上到下一层层给这棵树填节点，设 \(f_{i,j}\) 表示已经填了 \(i\) 个节点（我们不关心是第几层），最后一层有 \(j\) 个奇数个儿子的节点。
枚举这一层的节点数 \(k\)。那么上一层的 \(j\) 个节点均会被下取整掉一个儿子，这层与父亲奇偶性相同的节点总数为 \(t=\frac{k-j}{2}\)（奇偶性不对就不合法，跳过这个 \(k\)）。接下来我们需要知道当前层儿子数为奇数的节点个数。
枚举 \(p\) 表示这一层与父亲颜色相同的节点个数。那么我们至少需要 \(|t-p|\) 个奇数儿子的点才能放得下这 \(p\) 个节点。而更多的奇数点（\(|t-p|+2x\)）是没有意义的，因为我们并不关心下层的点具体每个怎么连，这对实际的贡献没有影响，是树形态不同但最终位置相同的重复解。理解上注意分清“有奇数个儿子”和“取反次数是奇数”。
故有转移：
时间复杂度 \(O(n^4)\)。
Code
#define int long long
const int N=105,mod=1e9+7;
int n,c[N][N],f[N][N];
il void init(int mx)
{
for(int i=0;i<=mx;i++)
for(int j=0;j<=i;j++) c[i][j]=j?(c[i-1][j-1]+c[i-1][j])%mod:1;
}
il void add(int &x,int y) {x=(x+y)%mod;}
signed main()
{
n=read(); init(n);
f[1][0]=f[1][1]=n;
for(int i=1;i<=n;i++)
for(int j=0;j<=i;j++)
{
if(!f[i][j]) continue;
for(int k=j?j:2;k<=n-i;k+=2)
{
int t=(k-j)>>1;
for(int p=0;p<=k;p++) add(f[i+k][abs(p-t)],f[i][j]*c[n-i][k]%mod*c[k][p]);
}
}
printf("%lld\n",f[n][0]);
return 0;
}
AGC023
D. Go Home
Tags: 博弈论
把问题倒过来，考虑车最后一个到的位置。不难发现这个位置只能是 \(1\) 或 \(n\)。
考虑车上的人的投票策略。
首先如果 \(S<X_1\) 或者 \(S>X_n\)，那么显然所有人希望车移动的方向都一样。且因为每到一个位置对应的人就会下车，答案即为车一直移动到另一端的距离。
剩下 \(X_1<S<X_n\) 的情况，如果 \(P_1\ge P_n\)，车一定先到 \(1\) 号楼，反之亦然。证明如下：
- 如果 \(X_{n-1}<S<X_n\)，显然除了 \(n\) 号楼的人所有人都想往左走；
- 如果 \(S<X_{n-1}\)，考虑走到 \(1\) 前是否经过了 \(n-1\)：如果经过了，就是上面的情况，否则也一定不会经过 \(n\)。
那么车到达 \(1\) 后会一直向右走到 \(n\)。也就是说 \(n\) 号楼的人的利益和 \(1\) 号楼是一致的，他们的共同目标是让 \(1\) 号楼的人尽可能早到。那么令 \(P_1\gets P_1+P_n\)，问题可以规约到只有 \([1,n-1]\) 号楼的情况。
如此递归至 \(S<X_l\) 或者 \(S>X_r\)，计算答案即可。时间复杂度 \(O(n)\)。
Code
#define int long long
const int N=1e5+5;
int n,s,x[N],p[N];
il int solve(int l,int r,int pos)
{
if(s<x[l]) return x[r]-s; if(s>x[r]) return s-x[l];
if(p[l]>=p[r])
{
p[l]+=p[r];
int res=solve(l,r-1,x[l]);
if(pos!=x[l]) res+=pos-x[l];
return res;
}
else
{
p[r]+=p[l];
int res=solve(l+1,r,x[r]);
if(pos!=x[r]) res+=x[r]-pos;
return res;
}
}
signed main()
{
n=read(),s=read();
for(int i=1;i<=n;i++) x[i]=read(),p[i]=read();
printf("%lld\n",solve(1,n,p[1]<p[n]?x[1]:x[n]));
return 0;
}
E. Inversions
Tags: 计数
为什么一写用线段树优化什么东西的题就调不出来呢？为什么呢？
令将 \(a\) 排序后的数组为 \(c\)，\(rk_i\) 表示 \(a_i\) 在数组 \(c\) 中对应的下标（\(a_i\) 的排名），\(pos_i\) 表示 \(c_i\) 在数组 \(a\) 中对应的下标（排名为 \(i\) 的数的位置）。
令 \(b_i=a_i-rk_i\)。那么可行的排列 \(p\) 的总方案数为
这个式子可以这样理解：考虑从小到大加入每个数 \(i\)，那么 \(i\) 有 \(c_i\) 个可以填的位置。由于这些位置中已经填了 \(i-1\) 个数，则 \(i\) 有 \(c_i-(i-1)\) 种填法。
考虑一对 \(j<i\) 的位置 \(i,j\) 对答案产生的贡献。
- 若 \(a_i\ge a_j\)，则 \(p_i\) 应当填小于 \(a_j\) 的数。看起来答案是
这不对，因为对于所有 \(a_j<a_k<a_i\)，\(a_k\) 都被前面的 \(a_i\) 多占了一个位置。因此正确的式子是
- 若 \(a_i<a_j\)，考虑容斥：答案是总方案数减去顺序对数，顺序对数就是把 \(i,j\) 反过来以后上一种情况的式子。
这样我们得到了 \(\mathcal{O}(n^2)\) 做法。
考虑优化，将上述只与 \(i\) 有关的部分拆出来：
按从小到大的顺序依次加入每个 \(a_i\)，我们只需要维护这个式子后半部分的区间和，即可求出答案。这需要支持区间乘和单点加，使用线段树维护。
同时因为要减掉 \(tot\)，还要顺便维护一下区间内已经被加入的数的个数。时间复杂度 \(\mathcal{O}(n\log n)\)。
Code
#define int long long
const int N=2e5+5,mod=1e9+7;
int n,a[N],b[N],rk[N],pos[N];
struct node{int x,id;} c[N];
il bool cmp(node x,node y) {return (x.x==y.x)?x.id<y.id:x.x<y.x;}
il int qpow(int n,int k=mod-2)
{
int res=1;
for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;
return res;
}
struct BIT
{
int tr[N];
il void add(int x,int k) {for(;x<=n;x+=x&(-x)) tr[x]+=k;}
il int query(int x) {int res=0;for(;x;x-=x&(-x)) res+=tr[x];return res;}
il int ask(int l,int r) {return query(r)-query(l-1);}
}tr;
struct segtree
{
int tr[N<<2],lz[N<<2];
#define ls (x<<1)
#define rs (x<<1|1)
#define mid (l+r>>1)
void build(int x,int l,int r)
{
lz[x]=1;
if(l==r) return;
build(ls,l,mid),build(rs,mid+1,r);
}
il void pushup(int x) {tr[x]=(tr[ls]+tr[rs])%mod;}
il void pushdown(int x)
{
tr[ls]=tr[ls]*lz[x]%mod,tr[rs]=tr[rs]*lz[x]%mod;
lz[ls]=lz[ls]*lz[x]%mod,lz[rs]=lz[rs]*lz[x]%mod;
lz[x]=1;
}
il void modify(int k) {tr[1]=tr[1]*k%mod,lz[1]=lz[1]*k%mod;}
void add(int x,int l,int r,int pos,int k)
{
if(l==r) {(tr[x]=tr[x]+k)%mod;return;}
pushdown(x);
if(pos<=mid) add(ls,l,mid,pos,k);
else add(rs,mid+1,r,pos,k);
pushup(x);
}
int query(int x,int l,int r,int ml,int mr)
{
if(ml>mr) return 0;
if(l==ml&&r==mr) return tr[x];
pushdown(x);
if(mr<=mid) return query(ls,l,mid,ml,mr);
else if(ml>mid) return query(rs,mid+1,r,ml,mr);
else return (query(ls,l,mid,ml,mid)+query(rs,mid+1,r,mid+1,mr))%mod;
}
}seg;
signed main()
{
n=read(); int tot=1;
seg.build(1,1,n);
for(int i=1;i<=n;i++) a[i]=c[i].x=read(),c[i].id=i;
sort(c+1,c+n+1,cmp);
for(int i=1;i<=n;i++) rk[c[i].id]=i,pos[i]=c[i].id;
for(int i=1;i<=n;i++)
{
b[i]=a[i]-rk[i],tot=tot*(b[i]+1)%mod;
if(b[i]+1<=0) {printf("0\n");return 0;}
}
int ans=0;
for(int x=1;x<=n;x++)
{
int i=pos[x];
int cnt=tr.ask(i+1,n);
int qwq=tot*qpow(2)%mod*qpow(b[i]+1)%mod;
ans+=qwq*seg.query(1,1,n,1,i-1)%mod+cnt*tot%mod-qwq*seg.query(1,1,n,i+1,n)%mod;
ans=(ans%mod+mod)%mod;
tr.add(i,1),seg.modify(b[i]*qpow(b[i]+1)%mod);seg.add(1,1,n,i,b[i]);
}
printf("%lld\n",ans);
return 0;
}
F. 01 on Tree
Tags: 贪心，Exchange Argument
其实这个奇怪名字的东西就是临项交换。
在树上删点不好做，我们考虑把过程倒过来：从 \(n\) 个点的初始状态开始，每个选择一个点，令它与原树上的父亲连边。这在原题意中表示删完父亲之后立即删除这个点所在的连通块。
那么在合并的过程中，同一个连通块内部的最少贡献是不变的。我们所要做的事情是合理地安排它们的顺序，使不同连通块之间的产生贡献最小。
设节点 \(a,b\) 所在连通块的 \(0,1\) 个数分别为 \(a_0,a_1,b_0,b_1\)，那么如果 \(a\) 排在 \(b\) 前面，跨过连通块的贡献为 \(a_1\times b_0\)。也就是说，\(a\) 排在 \(b\) 前面更优的条件是
即
故我们将连通块按照 \(\frac{a_1}{a_0}\) 的值从小到大进行合并即为最优方案。这可以使用大根堆维护。
Code
#define int long long
const int N=2e5+5;
int n,f[N];
int fa[N];
int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);}
int ans;
struct node
{
int x,cnt[2];
friend bool operator <(const node &x,const node &y)
{
return x.cnt[0]*y.cnt[1]<x.cnt[1]*y.cnt[0];
}
}a[N];
priority_queue<node> q;
void merge(int x,int y)
{
x=find(x),y=find(y);
if(x==y) return;
fa[y]=x;
ans+=a[x].cnt[1]*a[y].cnt[0];
a[x].cnt[1]+=a[y].cnt[1],a[x].cnt[0]+=a[y].cnt[0];
}
signed main()
{
n=read();
for(int i=2;i<=n;i++) f[i]=read();
for(int i=1;i<=n;i++)
{
fa[i]=i;
int x=read(); a[i].x=i;
a[i].cnt[x]++; q.push(a[i]);
}
while(!q.empty())
{
node u=q.top(); q.pop();
int x=find(u.x);
if(a[x].cnt[0]!=u.cnt[0]||a[x].cnt[1]!=u.cnt[1]) continue;
if(f[x])
{
merge(f[x],x);
q.push(a[find(f[x])]);
}
}
printf("%lld\n",ans);
return 0;
}
AGC024
D. Isomorphism Freak
Tags: 构造。
手玩一下样例，设这棵树的直径长度为 \(d\)，猜测第一问的答案是 \(\lceil\frac{d}{2}\rceil\)。
由于结论比较好猜到，这里略证一下：
- 对于一条长度为 \(d\) 的链，在不改变链长度的情况下链上的所有点只能两两对应，答案为 \(\lceil\frac{d}{2}\rceil\)。在链的尽头加点也一定不会让答案变小。
- 对于一棵树，我们找出它长度为 \(d\) 的直径，显然这是一个答案下界。我们令链的中点为树的根（如果中点是一条边其实也同理），只要补全叶子让所有深度相同的子树均同构，就可以保证深度相同的节点均同色，一定能够取到这个下界。
对于第二问，我们直接采用上文的构造，答案为每层最多的节点儿子数之积。
代码写麻烦了。
Code
#define int long long
const int N=105;
int n,f[N][2];
vector<int> e[N];
void dfs(int u,int fa)
{
f[u][0]=1;
for(auto v:e[u]) if(v^fa)
{
dfs(v,u);
if(f[v][0]+1>f[u][0]) f[u][1]=f[u][0],f[u][0]=f[v][0]+1;
else if(f[v][0]+1>f[u][1]) f[u][1]=f[v][0]+1;
}
}
int mxson[N],son[N],sum[N],lf[N],mxlf[N];
void solve(int u,int fa,int dep)
{
son[u]=0;int flag=1,sonlf=0; sum[dep]++;
for(auto v:e[u]) if(v^fa)
{
son[u]++,flag=0;
solve(v,u,dep+1);
if(lf[v]) {sonlf++;}
}
mxson[dep]=max(mxson[dep],son[u]),mxlf[dep]=max(mxlf[dep],sonlf);
lf[u]=flag;
}
signed main()
{
n=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
e[u].push_back(v),e[v].push_back(u);
}
int mx1=0,mx2=0,rt1=0,rt2=0;
for(int i=1;i<=n;i++)
{
dfs(i,0);
if(min(f[i][0],f[i][1])>mx1&&abs(f[i][0]-f[i][1])<=1)
{
mx2=mx1,rt2=rt1;
mx1=min(f[i][0],f[i][1]),rt1=i;
}
else if(min(f[i][0],f[i][1])>mx2&&abs(f[i][0]-f[i][1])<=1)
{
mx2=min(f[i][0],f[i][1]),rt2=i;
}
}
int mn=1e18;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++) lf[j]=0,mxlf[j]=0,mxson[j]=0,sum[j]=0;
solve(i,0,1);
if(!sum[mx1+1])
{
int ans=1;
for(int j=1;j<=n;j++) if(mxson[j]) ans*=mxson[j];
mn=min(ans,mn);
}
for(auto v:e[i])
{
for(int j=1;j<=n;j++) lf[j]=0,mxlf[j]=0,mxson[j]=0,sum[j]=0;
solve(i,v,1),solve(v,i,1);
if(sum[mx1+1]) continue;
int ans=2;
for(int j=1;j<=n;j++) if(mxson[j]) ans*=mxson[j];
mn=min(ans,mn);
}
}
printf("%lld %lld\n",mx1,mn);
return 0;
}
E. Sequence Growing Hard
Tags: dp，计数
AGC 好多神奇计数题。
先考虑这个问题：倒序操作，给定 \(A_n\)，求有多少不同的序列组 \((A_0,A_1,\dots,A_n)\)？
也就是说，我们要每次在序列中删一个数，使字典序递减。考虑数 \(i\) 在什么情况下可以被删掉，发现只有它后面第一个和它不一样的数比它小时，这步操作才是合法的。
而对于一段连续且相同的数，删掉它们中的任何一个都会得到相同的新序列。为避免计算重复，我们钦定这种情况下只能删一个连续段的最后一个。
那么限制变得简单了很多：只有 \(a_i>a_{i+1}\) 的数能够操作。
到了这一步还是不好 dp。根据 \(a_i>a_{i+1}\) 的限制从特殊值入手，发现 \(1\) 是只有作为末尾时才能成功删除的。这启发我们考虑序列里 \(1\) 的位置，并通过这个划分 dp 的子问题。
设 \(f_{i}\) 表示序列里已经有 \(i\) 个数的方案数。
枚举第一个 \(1\) 的位置 \(k\) 和被它删除的时间 \(p\)。那么根据上文，\([k+1,i]\) 位置上的数都应当在 \(p\) 时刻以前被删除。
一个新的问题是难以通过 dp 状态钦定「第一个 \(1\) 的位置」。考虑将值域塞进状态，设 \(f_{i,j}\) 表示序列里已经有 \(i\) 个数，它们的值域是 \([1,j]\) 的方案数。
那么让 \([1,k-1]\) 中没有 \(1\) 的方案数就是把 \(f_{k-1,j-1}\) 整体加上 \(1\) 的方案数。故有转移
直接 dp 的复杂度是 \(\mathcal{O}(n^4)\)，考虑交换求和顺序：
后面那个 \(\sum\) 与 \(j\) 无关，可以预处理。那么时间复杂度优化为 \(\mathcal{O}(n^3)\)。
Code
#define int long long
const int N=305;
int n,K,mod;
int f[N][N],g[N][N],c[N][N];
il void initc(int mx)
{
for(int i=0;i<=mx;i++)
for(int j=0;j<=i;j++) c[i][j]=j?(c[i-1][j-1]+c[i-1][j])%mod:1;
}
il void add(int &x,int y) {x+=y;if(x>=mod) x-=mod;}
signed main()
{
n=read(),K=read(),mod=read();
initc(n);
for(int i=0;i<=K;i++) f[0][i]=1;
for(int i=1;i<=n;i++)
for(int k=1;k<=i;k++)
for(int p=i-k+1;p<=i;p++) add(g[i][k],c[p-1][i-k]);
for(int i=1;i<=n;i++)
for(int j=1;j<=K;j++)
{
for(int k=1;k<=i;k++) add(f[i][j],f[i-k][j]*f[k-1][j-1]%mod*g[i][k]%mod);
add(f[i][j],f[i][j-1]);
}
printf("%lld\n",f[n][K]);
return 0;
}
F. Simple Subsequence Problem
Tags: 子序列自动机，dp
发现可能作为答案的字符串总数不多，只有 \(2^{n+1}\)，统计答案时可以暴力枚举。因此我们只要想办法求出每个 \(01\) 串是 \(S\) 中多少个字符串的子序列就可以了。
设 \(f_i\) 表示字符串 \(i\) 是 \(S\) 中多少个字符串的子序列。但这样显然是没法转移的：下一个状态由字符串 \(i\) 添加一个字符得到，会重复计数。
考虑把子序列自动机的匹配过程压进 dp 状态。设 \(f(A \texttt{|} B)\) 表示 \(S\) 集合中，满足子序列自动机上已匹配的部分为 \(A\)，未匹配的部分为 \(B\) 的方案数。
举个例子，\(f(\texttt{10|1101})\) 可以向以下状态转移：
- 匹配一个 \(\texttt{1}\)，有 \(f(\texttt{10|1101})\to f(\texttt{101|101})\)；
- 匹配一个 \(\texttt{0}\)，有 \(f(\texttt{10|1101})\to f(\texttt{100|1})\)；
- 在当前位置结束匹配，有 \(f(\texttt{10|1101})\to f(\texttt{10|})\)。
那么字符串 \(s\) 作为子序列的出现次数为 \(f(s\texttt{|})\)。
对于初始属于 \(S\) 的字符串 \(t\)，有初始状态 \(f(\texttt{|}t)=1\)。
一个状态可以由整个字符串和分隔线位置唯一确定。但因为字符串有前导 \(0\)，直接记序列长度会使空间复杂度变成 \(\mathcal{O}(2^nn^2)\)，存不下。不过实际上的总字符串数只有 \(2n\)，可以通过预处理标号将空间复杂度去掉一个 \(n\)。
Code
const int N=(1<<20)+5;
int n,K;
int id[21][N],f[21][N<<1];
int len[N<<1],s[N<<1];
int main()
{
n=read(),K=read(); int tot=0;
for(int i=0;i<=n;i++)
for(int j=0;j<(1<<i);j++)
{
char c; cin>>c;
id[i][j]=++tot,f[0][tot]=c-'0';
len[tot]=i,s[tot]=j;
}
for(int i=0;i<=n;i++)
{
for(int j=1;j<=tot;j++)
{
int l=len[j],s=::s[j];
if(!f[i][j]||i>=l) continue;
int A=0; //none
for(int k=l-1;k>=l-i;k--) A=(A<<1)|(s>>k&1);
f[i][id[i][A]]+=f[i][j];
int pos=-1; //1
for(int k=l-i-1;k>=0;k--) if(s>>k&1) {pos=k;break;}
if(pos!=-1)
{
int B=A<<1|1;
for(int k=pos-1;k>=0;k--) B=(B<<1)|(s>>k&1);
f[i+1][id[i+1+pos][B]]+=f[i][j];
}
pos=-1; //0
for(int k=l-i-1;k>=0;k--) if(!(s>>k&1)) {pos=k;break;}
if(pos!=-1)
{
int B=A<<1;
for(int k=pos-1;k>=0;k--) B=(B<<1)|(s>>k&1);
f[i+1][id[i+1+pos][B]]+=f[i][j];
}
}
}
int ans=0,anslen=0;
for(int i=1;i<=tot;i++)
if(f[len[i]][i]>=K&&anslen<len[i]) anslen=len[i],ans=s[i];
for(int i=anslen-1;i>=0;i--) printf("%d",ans>>i&1); printf("\n");
return 0;
}
AGC025
D. Choosing Points
Tags: 构造，二分图
考虑只有一个 \(D\) 的限制的情况怎么做。将图上所有距离恰为 \(\sqrt{D}\) 的整点之间连边，会得到一张二分图。
接下来证明这个结论。这里我们钦定边的其中一个起点是 \((0,0)\)，其余连边都可以平移得到。
将 \(D\) 表示为 \(4^p\times q\ (q\bmod 4\neq 0)\) 的形式，那么边的另一端 \((x,y)\) 可以表示为 \((2^p\times a,2^p\times b)\)。根据 \(q\bmod 4\) 的值分类讨论：
- \(q\bmod 4=1\)，则 \(a\) 和 \(b\) 奇偶性不同。这说明 \(x,y\) 奇偶性相同的点只会向奇偶性不同的点连边，这两个集合独立。
- \(q\bmod 4=2\)，则 \(a\bmod 2=1\) 且 \(b\bmod 2=1\)。这时 \(x,y\) 奇偶性相同的点只会向奇偶性相同的点连边。
- \(q\bmod 4=3\)，但 \(a,b\bmod 2\in [0,1]\)。因此这种情况不存在。
对两个 \(D\) 分别建立二分图并染色，根据两个图上的颜色一共可以把点分为四类。那么 \(4n^2\) 个点中至少有一类不少于 \(n^2\) 个，找到这一类并输出即可。
Code
const int N=605;
int n,D1,D2,col[N][N],cnt[N],vis[N][N];
typedef pair<int,int> pir;
vector<pir> v;
int dx[4]={1,-1,1,-1};
int dy[4]={-1,1,1,-1};
void dfs(int x,int y,int tp)
{
if(tp==2) cnt[col[x][y]]++;
for(int w=0;w<4;w++)
for(auto &[Dx,Dy]:v)
{
int nx=x+Dx*dx[w],ny=y+Dy*dy[w];
if(nx<0||ny<0||nx>=(n<<1)||ny>=(n<<1)||vis[nx][ny]) continue;
int ncol=(col[x][y]&tp)^tp;
col[nx][ny]^=ncol,vis[nx][ny]=1,dfs(nx,ny,tp);
}
}
void get(int D,int tp)
{
v.clear();
for(int i=0;i<(n<<1);i++)
for(int j=0;j<(n<<1);j++)
{
vis[i][j]=0;
if(i*i+j*j==D) v.push_back(pir(i,j));
}
for(int i=0;i<(n<<1);i++)
for(int j=0;j<(n<<1);j++)
if(!vis[i][j]) dfs(i,j,tp);
}
int main()
{
n=read(),D1=read(),D2=read();
get(D1,1);get(D2,2);
for(int i=0;i<4;i++) if(cnt[i]>=n*n)
{
int tot=0;
for(int x=0;x<(n<<1);x++)
for(int y=0;y<(n<<1);y++)
{
if(tot==n*n) break;
if(col[x][y]==i) tot++,printf("%d %d\n",x,y);
}
break;
}
return 0;
}
E. Walking on a Tree
先考虑如果所有树边都被偶数条路径覆盖怎么做。
对于每条路径，连 \(x_i\to y_i\) 的无向边。那么每个点的度数都为偶数，也就是每个连通子图都存在欧拉回路。我们先跑出欧拉回路，再根据回路中每条路径连的边被经过的方向来定向，则所有树边正反通过次数相同。
这个结论的证明就是对于一条树边 \((u,v)\)，我们把这棵树上的点划分成不经过这条边的两部分。因为我们没连树边，路径从 \(u\) 一侧到 \(v\) 一侧必须要经过一条路径边，又因为是回路，连接这两部分之间的边正反向通过的次数一定相同。
还需要覆盖次数不全是偶数的情况。这时我们需要补一些边使所有点度数都是偶数。
仿照 [省选联考 2020 B 卷] 丁香之路 的思路，考虑从下到上 dfs 处理原树：如果处理完子树 \(u\)，点 \(u\) 的度数仍是奇数，则连一条 \(u\to fa_u\) 的无向边。
和之前同理，可以证明这样每条树边正反通过次数至多差 \(1\)，为最优解。
给所有边定向后，树上差分（或直接暴力）即可统计所有树边的权值和。代码长是因为粘了一堆板子。
Code
const int N=10005;
typedef pair<int,int> pir;
map<pir,int> mp;
int n,m;
struct edge{int nxt,to;} e[N<<1];
int head[N],cnt=1;
il void add(int u,int v) {e[++cnt]={head[u],v};head[u]=cnt;}
vector<int> E[N];
struct LCA
{
int dfn[N],fa[N],tot,dep[N],st[20][N];
il int get(int x,int y) {return dep[x]<dep[y]?x:y;}
void dfs(int u,int ff)
{
dfn[u]=++tot,st[0][tot]=ff,fa[u]=ff; dep[u]=dep[ff]+1;
for(auto v:E[u]) if(v^ff) dfs(v,u);
}
il void init()
{
dfs(1,0);
for(int i=1;(1<<i)<=n;i++)
for(int j=1;j<=n-(1<<i)+1;j++)
st[i][j]=get(st[i-1][j],st[i-1][j+(1<<i-1)]);
}
il int lca(int x,int y)
{
if(x==y) return x;
if((x=dfn[x])>(y=dfn[y])) swap(x,y);
int l=__lg(y-x);
return get(st[l][x+1],st[l][y-(1<<l)+1]);
}
}l;
int ans[N],St[N],Ed[N],vis[3][N],Vis[N<<1],deg[N];
int flag[N];
void getedge(int u)
{
for(auto v:E[u]) if(v^l.fa[u])
{
getedge(v);
if(deg[v]&1) deg[v]++,deg[u]++,add(u,v),add(v,u);
}
}
vector<int> stk;
void dfs(int u)
{
flag[u]=1;
for(int &i=head[u];i;i=e[i].nxt)
{
int v=e[i].to; if(Vis[i]) continue;
Vis[i]=Vis[i^1]=1,dfs(v);
}
stk.push_back(u);
}
void getvis(int u,int fa)
{
for(auto v:E[u]) if(v^fa)
getvis(v,u),vis[0][u]+=vis[0][v],vis[1][u]+=vis[1][v];
}
int main()
{
n=read(),m=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
E[u].push_back(v),E[v].push_back(u);
}
l.init();
for(int i=1;i<=m;i++)
{
int u=read(),v=read(); St[i]=u,Ed[i]=v;
add(u,v),add(v,u); deg[u]++,deg[v]++;
mp[pir(u,v)]=i,mp[pir(v,u)]=-i;
}
getedge(1);
for(int i=1;i<=n;i++) if(!flag[i]) dfs(i);
reverse(stk.begin(),stk.end());
for(int i=0;i+1<stk.size();i++)
if(mp.count(pir(stk[i],stk[i+1])))
{
int x=mp[pir(stk[i],stk[i+1])];
ans[abs(x)]=x>0?0:1;
}
for(int i=1;i<=m;i++)
{
int u=St[i],v=Ed[i],x=ans[i];
vis[x][u]++,vis[x][l.lca(u,v)]--;
vis[x^1][v]++,vis[x^1][l.lca(u,v)]--;
}
getvis(1,0);
int res=0;
for(int i=1;i<=n;i++) res+=(vis[0][i]!=0)+(vis[1][i]!=0);
printf("%d\n",res);
for(int i=1;i<=m;i++)
if(ans[i]==0) printf("%d %d\n",St[i],Ed[i]);
else printf("%d %d\n",Ed[i],St[i]);
return 0;
}
本文来自博客园，作者：樱雪喵，转载请注明原文链接：https://www.cnblogs.com/ying-xue/p/AGC020-025.html
