Splay 详细图解 & 轻量级代码实现
学 LCT 发现有点记不得 Splay 怎么写,又实在不知道这篇博客当时写了些什么东西(分段粘代码?),决定推倒重写。
好像高一学弟也在学平衡树,但相信大家都比樱雪喵强,都能一遍学会!/kel
写在前面
整合了一些各种地方看到的 corner case,和我学的时候想不明白题解却说显然的东西。
Splay 的实现方式多种多样,这里只讲我比较喜欢的写法。部分参考 Cx330 神仙的板子,拜谢。
不过基本原理上都是一样的,无需担心这个问题。学原理的建议就是多动笔自己画每棵树是怎么转。
这篇博客也画了很多图,算是给曾经对着网上几乎没图的博客画了一大堆东西也搞不明白 Splay 应该怎么转的自己一个交代?
二叉搜索树
在学习 Splay 之前,我们要先知道二叉搜索树的基本概念。
定义
- 是一棵有根且点上带权值的二叉树
- 空树是二叉搜索树
- 若根节点左子树不为空,则左子树内点的权值均小于根节点的权值
- 若根节点右子树不为空,则右子树内点的权值均大于根节点的权值
换句话说,中序遍历这棵二叉树,得到点的权值序列单调不降。比如这样:
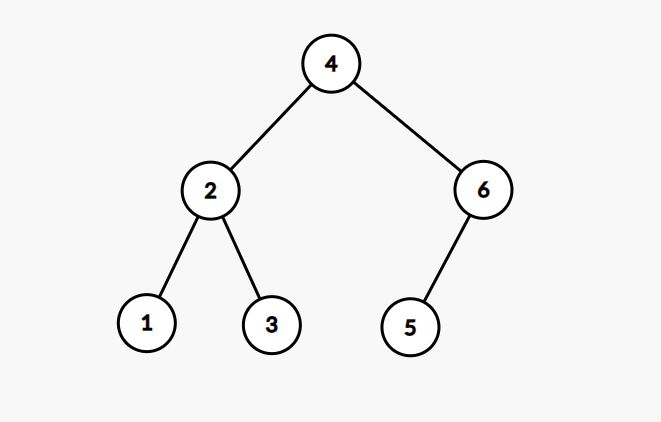
这里要注意区分点的权值和编号,我们要求单调不降的是点的权值,不是编号。下文出现的所有图,点上的数字均表示权值。
用途
「二叉搜索树」,用来做的事情自然是搜索。具体地,它可以支持插入、删除、查询前驱后继、查询给定值在序列中的排名、查询特定排名的数字值等操作。
对于一个序列中多个权值相同的点,有两种处理方式:
- 对树上的每个点记录 ,表示该点的权值在序列中出现了几次;
- 直接把多个权值相同的点都塞到树上。
第二种做法并不严格符合上文所述二叉搜索树的定义,但鉴于它能减少大量的特判,我们就先不计较这个问题。
这里樱雪喵擅自把定义改成「左子树权值不大于根节点,右子树权值不小于根节点」好了。
插入节点
我们考虑不改变树的原有结构,把新的点接在某个旧点下面。从根节点开始,我们依次考虑新加的这个点应该在哪个子树里:
- 权值小于当前节点,则递归左子树;
- 大于当前节点,则递归右子树;
- 等于当前节点,理论上去哪边都行,就先钦定它往左边放吧。
走到叶子节点时,把这个新点接在下面就好了。时间复杂度是 的,其中 表示树高。
删除节点
形如插入节点,我们先通过权值大小沿着树走,找到这个要被删除的点的位置。
这里可能要稍稍麻烦一点:
- 如果这个点没有儿子,那直接删掉;
- 只有一个儿子,我们直接把它的儿子和它的父亲连在一起。比如说删点 :
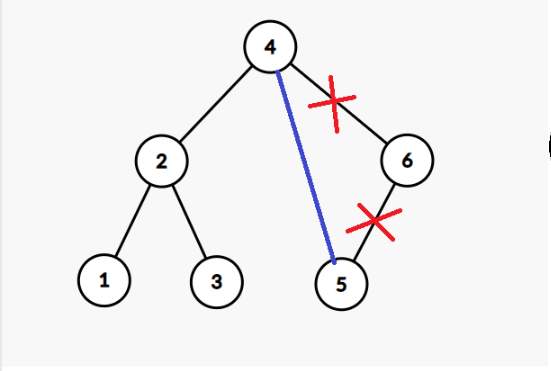
- 它有两个儿子就比较难办。为了说得明白一点这里又重新画了一棵树,比如说我们要删点 。
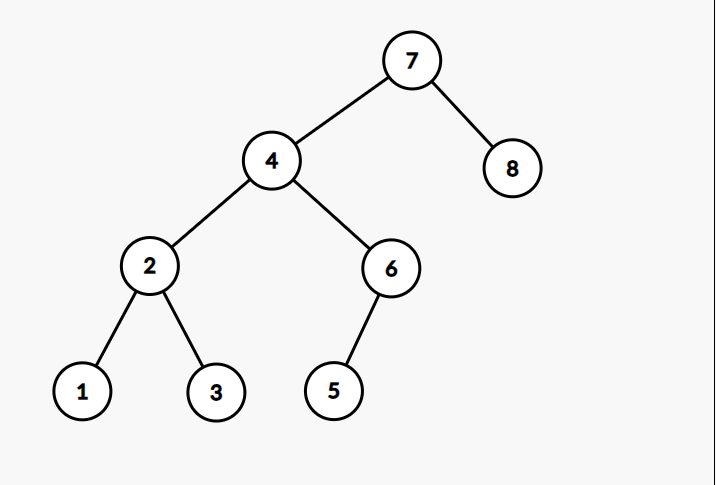
先把 及和它相连的边删掉,再考虑怎么把剩下的点重新接成一棵树。
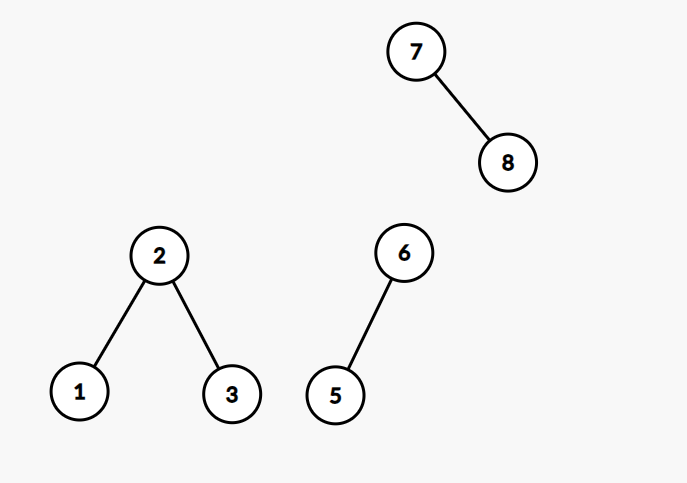
这种情况的处理方法一般是钦定一边的儿子来接替这个点的位置,这里我们钦定把左儿子接上来。
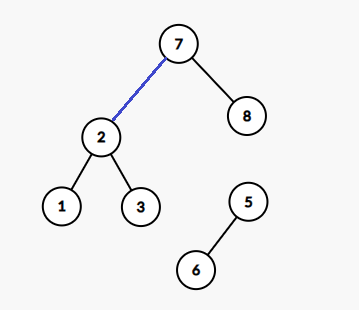
剩下的右子树怎么办呢?它肯定不能接在自己原来的位置上,因为接替 的 已经有右儿子了。根据二叉搜索树的性质,右子树的所有权值都大于左子树,所以我们把右子树整个接到(左子树里权值最大的那个点)的右儿子上。显然这个权值最大的点是没有右儿子的,因为不然它就不是最大的。
那这棵树长成了这样:
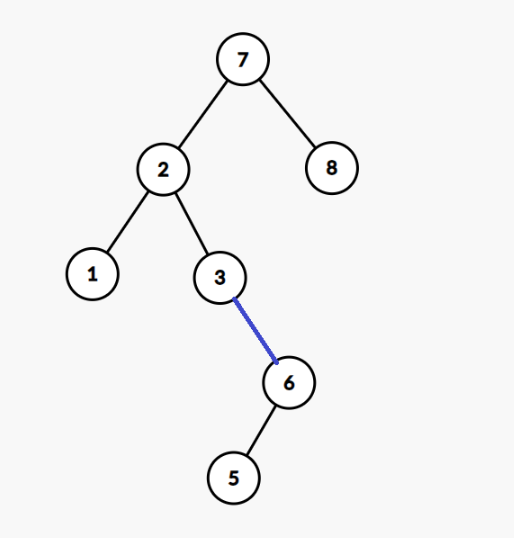
至此我们成功删除了 这个节点,并且依然满足二叉搜索树的性质。
至于查询操作各有不同,留到后面 Splay 的部分再逐一细说。
但根据上面两个操作也可以大致想象:朴素的二叉搜索树维护这些操作的时间复杂度都是 的。
在正常情况下,树高不会太高,似乎并没有什么大问题;但我们可以构造一些数据让树变得很高。
考虑依次对树插入节点 ,根据上面插入操作的流程,这棵树就会变成这样:
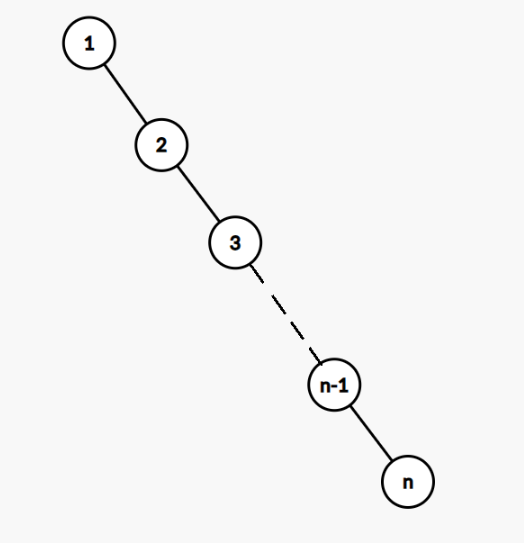
可见它的树高变成了 ,插入的复杂度也变成了 ,并不比暴力做法高效。
对于同一个序列,能构成合法的二叉搜索树有很多种形态,我们要保证自己构造的这棵树不出现上面的情况。
平衡树就是解决这个问题的算法。顾名思义,找一种调整方法让这棵二叉搜索树平衡,保持它的高度为 ,从而保证各个操作的时间复杂度。
Splay
Splay 的核心是通过对一些节点进行旋转,改变这棵树的结构,让它趋于平衡。
接下来将对操作和模板代码进行分段讲解。(原来这里只有代码没有讲解,所以等同于完全重写
一些基础操作 & 准备
这里我们先不考虑怎么转,只把它当个普通的二叉搜索树,把节点维护的信息定义出来。
实现上,可以如下文写一个结构体,也可以直接开一堆数组。前者的逻辑更清晰,但考虑到后文的大量调用,开一堆数组写起来码量会少一些。
当然也可以跟樱雪喵一样写几个 define(?
struct tree
{
int s[2],siz,fa,key;
tree(){s[0]=s[1]=siz=fa=key=0;}
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
然后实现几个简单的函数。
il int newnode(int key) {tr[++idx].key=key,tr[idx].siz=1;return idx;} //新建一个权值为 key 的节点
il void maintain(int x) {tr[x].siz=tr[ls(x)].siz+tr[rs(x)].siz+1;} //更新子树 size
il void clear(int x) {ls(x)=rs(x)=fa(x)=tr[x].siz=tr[x].key=0;} //清空一个节点(用于删除)
il bool get(int x) {return x==rs(fa(x));} //求 x 是它父亲的哪个儿子
rotate 操作
rotate 操作的本质是把某个给定节点上移一个位置,并保证二叉搜索树的性质不改变。
在 Splay 中,旋转操作分为左旋(Zag) 和右旋(Zig)。(这张图是从 OI-wiki 贺的,他点上标的是编号而不是权值。)
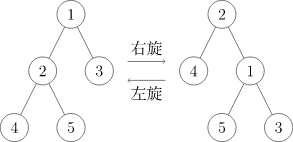
发现旋转时,不只是简单地改变根节点,还改变了树的结构。或许看了上图令人迷惑,我们分步演示一个 Splay 的右旋操作步骤。
对于下面这棵树的点 执行 操作,可以想象最后 会变成 的右儿子,所以先把 现在的右儿子断开,连到 下面:
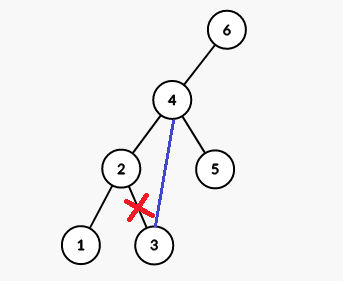
接下来,我们把 移到 上面,让它成为 的父亲:
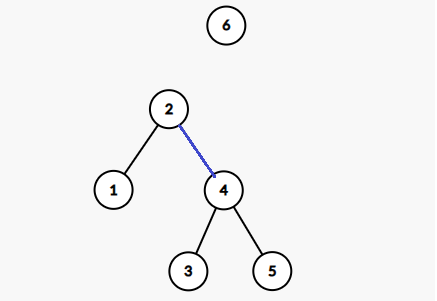
这一步上,虽然树的形态(连边状态)不改变,但平衡树是有根树,我们改变的是儿子和父亲的关系。
最后,把 和原来 的父亲 连起来:
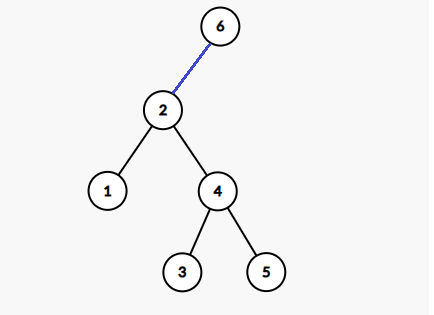
这时候我们就成功把点 上移了一个位置,而且保证了中序遍历没变。
代码实现时无需区分左旋和右旋,因为它们本质上都是根据 是父亲的哪个儿子进行的方向判断。操作完成后,要更新节点的 信息。
il void rotate(int x)
{
int y=fa(x),z=fa(y); int c=get(x); // x 在父亲的哪个方向
if(tr[x].s[c^1]) fa(tr[x].s[c^1])=y; // 把 x 相反方向的儿子接在 y 上,可以对照上文的图理解一下
tr[y].s[c]=tr[x].s[c^1],tr[x].s[c^1]=y,fa(y)=x,fa(x)=z;
if(z) tr[z].s[y==tr[z].s[1]]=x; //这里千万不要想当然改成 get(y)!因为 fa(y) 已经不是 z 了。
maintain(y),maintain(x);
}
upd: 这只猫敲板子又把 if(z) tr[z].s[y==tr[z].s[1]]=x; 写错了。避雷避雷避雷!
Splay 操作
的作用是把点 一路旋到根上。这里我们分为 种情况来讨论 应该怎么转。
Zig / Zag
最简单的情况是 现在的深度为 ,那么我们直接执行 rotate(x) 即可。这张图应该不会造成啥理解障碍,直接贺过来了。
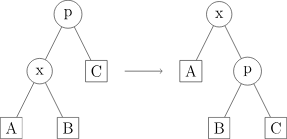
Zig-Zag / Zag-Zig
这种情况也比较直观。设 。如果 和 相对于各自的父亲是不同方向的,我们就对它们执行 Zig-Zag 或 Zag-Zig 操作。
比如这棵树长这个样子。
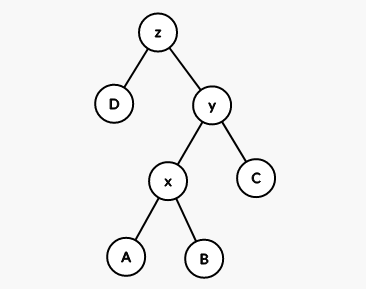
我们先执行 rotate(x),变成这样:
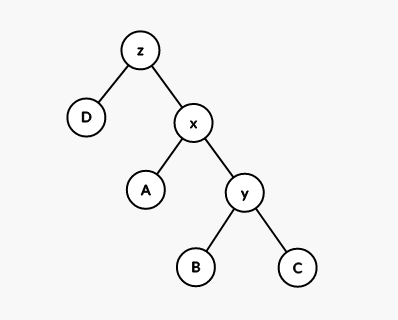
然后再执行一次 rotate(x),就把 一共往上移了两个位置。
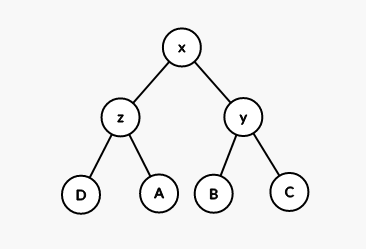
Zig-Zig / Zag-Zag
依然设 。如果 和 相对于各自的父亲是同向的,我们就对它们执行 Zig-Zig 或 Zag-Zag 操作。
以 Zig-Zig 操作为例,树在转之前长这样:
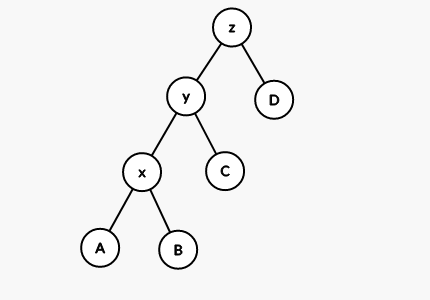
我们规定,这种情况下先转 再转 ,而不是上文那样转两次 (这么做的原因真的显然吗?)。这是用于保证复杂度的,后文 Spaly 部分会对其进行分析。
先 rotate(y):
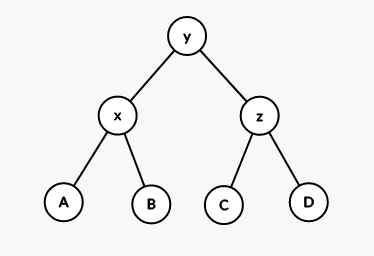
再 rotate(x):
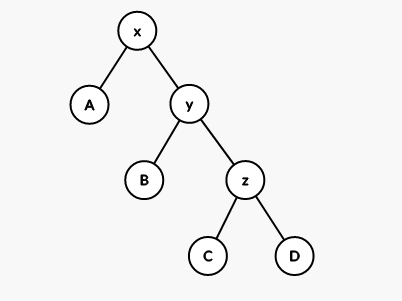
至此讲完了 Splay 的 种操作,而 Splay 函数的代码实现实际上很短。
il void splay(int x)
{
for(int f=fa(x);f=fa(x),f;rotate(x)) // 不论哪个操作,最后一步都是 rotate(x)
if(fa(f)) rotate(get(f)==get(x)?f:x); // 判断转 y 还是转 x
rt=x;
}
这里放一段 Xu_brezza 学长写的注释。感觉有点乐的。原文链接
void rotate(int x){//旋转操作
int y = fa[x],z = fa[y],chk = get(x);//爹,爹的爹,是爹的哪个儿子
ch[y][chk] = ch[x][chk^1];//如果我是爹的左儿子,把我的右儿子给爹的左儿子//如果是右儿子,把我的左儿子给爹的右儿子
if(ch[x][chk^1])fa[ch[x][chk^1]] = y;//把这个儿子的爹改成我的爹
ch[x][chk^1] = y;//父子关系换了,哈哈!
fa[y] = x;fa[x] = z;//哈哈!哈哈!
if(z)ch[z][y == ch[z][1]] = x;//如果爹的爹存在,更新儿子,你滴儿子是我辣!
maintain(x);maintain(y);//pushup pushup
}
void splay(int x){
for(int f;f = fa[x];rotate(x))//我还有爹吗,有就旋
if(fa[f])rotate(get(x) == get(f) ? f : x);//如果有爹,相同的话要先旋爹
root = x;//我是根辣!
}
为保证 Splay 的复杂度,我们规定每次操作最后访问到的节点是 ,都要把 Splay 到根。
时间复杂度分析
比较复杂,需要用到势能分析。这里挂个 Link,神仙们有兴趣可以去看看。
这里就不证一遍了(让我证我也只会对着 OIwiki 贺),记下来它是 的就可以。
单旋 Spaly
上面我们学的 Splay 是双旋的,也就是根据 和 是否同向分为两种不同的操作。我曾经很不理解为什么不一直只转 ,不知道大家刚学的时候会不会这么想。
实际上确实有只转 的这个东西,它叫 Spaly,和 Splay 的区别就是单旋还是双旋。但这玩意的时间复杂度是假的,举个例子:
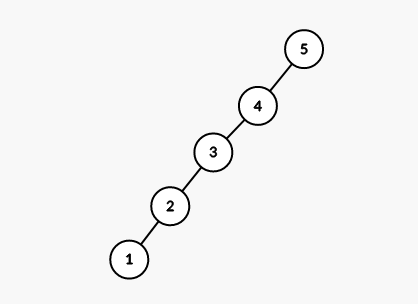
这棵树退化成了链,我们显然希望通过旋转操作让它不再是链。但是如果单旋,先 spaly(1),发现还是一条链;
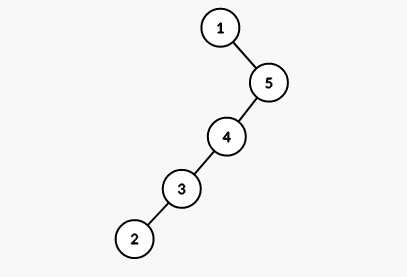
我们再试试接下来 spaly(2),结果还是一条链。
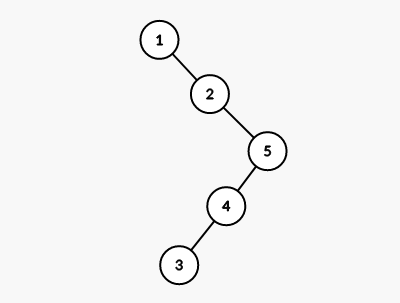
可以自己画画图模拟转的过程,就会发现它完全没有起到平衡的作用。
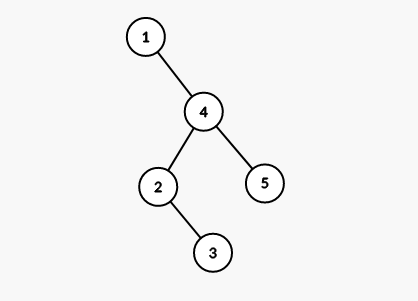
而对原链进行 Splay(1),即先后 rotate 2,1,4,1,发现这棵树操作完改变了结构,不是一条链。这是我们希望看到的。
应用
学完了 Splay 的核心操作,插入删除查找什么的就和二叉搜索树没啥区别了。
这里一个一个操作说。
实现上,我的原则是在各个操作不互相依赖的情况下减少码长。虽然相互依赖能写出代码很短的板子(1.7k?),但如果题里只要求实现一部分操作,你还要把不用的也写上,就很不合算。
哦吐槽一句 OIwiki 的板子又互相依赖又写得很长。打算照着学的快跑,希望不要有人跟我一样费好大劲去背那个阴间板子。
插入
和前面二叉搜索树一样,唯一的区别是最后 Splay(x)。所以直接放代码:
il void ins(int key)
{
int now=rt,f=0;
while(now) f=now,now=tr[now].s[key>tr[now].key];
now=newnode(key),fa(now)=f,tr[f].s[key>tr[f].key]=now,splay(now);
}
删除
似乎这个东西大部分人的写法都依赖查询排名的函数,所以一般被放到最后讲。不过樱雪喵的板子貌似没有这个问题,于是直接按顺序放在了这里。
前面详细讲过了二叉搜索树怎么删点,依然直接给出代码:
别被吓跑,delete 是全文代码最长的操作了,剩下的都很短 QAQ。
upd: 直接 return 的复杂度假了,感谢评论区大佬指出。
il void del(int key)
{
int now=rt,p=0;
while(tr[now].key!=key&&now) p=now,now=tr[now].s[key>tr[now].key]; // 找到要删除的这个点
if(!now) {splay(p);return;}
splay(now); int cur=ls(now);
if(!cur) {rt=rs(now),fa(rs(now))=0,clear(now);return;} //没有左儿子,摆
while(rs(cur)) cur=rs(cur);
rs(cur)=rs(now),fa(rs(now))=cur,fa(ls(now))=0,clear(now); //把右儿子接在(左子树的最大权值)下面
maintain(cur),splay(cur);
}
查询 的排名
从根节点开始,根据左子树的 判断我们查询的 在哪边的子树里;因为一个平衡树里可能有一堆权值是 的点,这里我们本质上要找的是 严格小于 的点数 。
每次往右子树走,左边的子树就给答案贡献了 个比 小的数。
il int rnk(int key)
{
int res=1,now=rt,p;
while(now)
if(p=now,tr[now].key<key) res+=tr[ls(now)].siz+1,now=rs(now);
else now=ls(now);
return splay(p),res;
}
注意,这里虽然只是在树上跑点,没有改变平衡树的结构,但依然要进行 Splay。
考虑构造这样的数据:依次在树上插入 ,画一下可以发现即使每次插入完都有在 Splay,它也还是一条链。当然这对插入的时间复杂度没有影响,因为每次根节点的右儿子都是空的,不会递归到链里。
但这对查询操作有影响啊。考虑插入完反复查询排名为 的数,单次复杂度就一直是 。于是就寄了!
而查询完 Splay 一下,这棵树就不再是一条链,保证了后续操作的均摊复杂度。
查询排名为 的数
同理,根据子树 直接判断排名为 的数走哪一边即可。
il int kth(int rk)
{
int now=rt;
while(now)
{
int sz=tr[ls(now)].siz+1;
if(sz>rk) now=ls(now);
else if(sz==rk) break;
else rk-=sz,now=rs(now);
}
return splay(now),tr[now].key;
}
查询 的前驱
前驱,定义为序列里最大的比 小的数。
一个写起来比较短的办法是,先插入一个 ,这样 就是根了;那 的前驱,就是先走根的左儿子,然后再一直走右儿子走到底。最后再删掉插入的这个 。
但是删除操作不好写,很多时候题面也不要求删除。我们换一种办法。
考虑从根往下走,如果当前点大于等于 ,那前驱一定在左子树,我们往左走;否则,前驱可能在这个点,也可能在这个点的右子树里,总之不在左子树里。所以先用这个点更新答案,再进入它的右子树继续找。
也麻烦不了多少。
il int pre(int key)
{
int now=rt,ans=0,p;
while(now)
if(p=now,tr[now].key>=key) now=ls(now);
else ans=tr[now].key,now=rs(now);
return splay(p),ans;
}
查询 的后继
后继就是最小的比 大的数,把前驱的做法反过来即可,不再赘述。
il int nxt(int key)
{
int now=rt,ans=0,p;
while(now)
if(p=now,tr[now].key<=key) now=rs(now);
else ans=tr[now].key,now=ls(now);
return splay(p),ans;
}
到这里就足以过掉 lg P3369 【模板】普通平衡树 了。
完整板子如下:
#include<bits/stdc++.h>
#define il inline
using namespace std;
il int read()
{
int xr=0,F=1; char cr;
while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
while(cr>='0'&&cr<='9')
xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
return xr*F;
}
const int N=1e5+5;
struct tree
{
int s[2],siz,fa,key;
tree(){s[0]=s[1]=siz=fa=key=0;}
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
int rt,idx;
il int newnode(int key) {tr[++idx].key=key,tr[idx].siz=1;return idx;}
il void maintain(int x) {tr[x].siz=tr[ls(x)].siz+tr[rs(x)].siz+1;}
il void clear(int x) {ls(x)=rs(x)=fa(x)=tr[x].siz=tr[x].key=0;}
il bool get(int x) {return x==rs(fa(x));}
il void rotate(int x)
{
int y=fa(x),z=fa(y); int c=get(x);
if(tr[x].s[c^1]) fa(tr[x].s[c^1])=y;
tr[y].s[c]=tr[x].s[c^1],tr[x].s[c^1]=y,fa(y)=x,fa(x)=z;
if(z) tr[z].s[y==tr[z].s[1]]=x; //not get(y)!
maintain(y),maintain(x);
}
il void splay(int x)
{
for(int f=fa(x);f=fa(x),f;rotate(x))
if(fa(f)) rotate(get(f)==get(x)?f:x);
rt=x;
}
il void ins(int key)
{
int now=rt,f=0;
while(now) f=now,now=tr[now].s[key>tr[now].key];
now=newnode(key),fa(now)=f,tr[f].s[key>tr[f].key]=now,splay(now);
}
il void del(int key)
{
int now=rt,p=0;
while(tr[now].key!=key&&now) p=now,now=tr[now].s[key>tr[now].key];
if(!now) {splay(p);return;}
splay(now); int cur=ls(now);
if(!cur) {rt=rs(now),fa(rs(now))=0,clear(now);return;}
while(rs(cur)) cur=rs(cur);
rs(cur)=rs(now),fa(rs(now))=cur,fa(ls(now))=0,clear(now);
maintain(cur),splay(cur);
}
il int pre(int key)
{
int now=rt,ans=0,p;
while(now)
if(p=now,tr[now].key>=key) now=ls(now);
else ans=tr[now].key,now=rs(now);
return splay(p),ans;
}
il int nxt(int key)
{
int now=rt,ans=0,p;
while(now)
if(p=now,tr[now].key<=key) now=rs(now);
else ans=tr[now].key,now=ls(now);
return splay(p),ans;
}
il int rnk(int key)
{
int res=1,now=rt,p;
while(now)
if(p=now,tr[now].key<key) res+=tr[ls(now)].siz+1,now=rs(now);
else now=ls(now);
return splay(p),res;
}
il int kth(int rk)
{
int now=rt;
while(now)
{
int sz=tr[ls(now)].siz+1;
if(sz>rk) now=ls(now);
else if(sz==rk) break;
else rk-=sz,now=rs(now);
}
return splay(now),tr[now].key;
}
int main()
{
int T=read();
while(T--)
{
int op=read(),x=read();
if(op==1) ins(x);
if(op==2) del(x);
if(op==3) printf("%d\n",rnk(x));
if(op==4) printf("%d\n",kth(x));
if(op==5) printf("%d\n",pre(x));
if(op==6) printf("%d\n",nxt(x));
}
return 0;
}
附一个樱雪喵早年间写的 OIwiki 版本 Splay。可以在码风基本相同的情况下对比看看区别(?
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
struct node{
int fa,s[2],siz,cnt,w;
}t[N];
int rt,tot;
void getsiz(int x) {t[x].siz=t[t[x].s[0]].siz+t[t[x].s[1]].siz+t[x].cnt;}
int gets(int x) {return x==t[t[x].fa].s[1];}
void clear(int x) {t[x].fa=t[x].s[0]=t[x].s[1]=t[x].siz=t[x].cnt=t[x].w=0;}
void turn(int x)
{
int y=t[x].fa,z=t[y].fa;bool chk=gets(x);
if(t[x].s[chk^1]) t[t[x].s[chk^1]].fa=y;
t[y].s[chk]=t[x].s[chk^1];
t[x].s[chk^1]=y;t[y].fa=x;t[x].fa=z;
if(z) t[z].s[y==t[z].s[1]]=x;
getsiz(y);getsiz(x);
rt=x;
}
void splay(int x)
{
for(int f=t[x].fa;f=t[x].fa,f;turn(x))
if(t[f].fa) turn(gets(x)==gets(f)?f:x);
rt=x;
}
void insert(int k)
{
if(!rt)
{
t[++tot].w=k;t[tot].cnt=1;getsiz(tot);
rt=tot;return;
}
int now=rt,f=0;
while(1)
{
//cout<<now<<" "<<t[now].w<<endl;
if(t[now].w==k) {t[now].cnt++;getsiz(now),getsiz(f);splay(now);return;}
f=now;now=t[f].s[k>t[f].w];
if(!now)
{
now=++tot;
t[now].w=k,t[now].fa=f,t[f].s[k>t[f].w]=now;
t[now].cnt=1;getsiz(now),getsiz(f);
splay(now);return;
}
}
}
int rnk(int k)
{
int now=rt,ans=0;
while(1)
{
if(k<t[now].w) {now=t[now].s[0];continue;}
ans+=t[t[now].s[0]].siz;
if(k==t[now].w) {splay(now);return ans+1;}
ans+=t[now].cnt;now=t[now].s[1];
}
}
int kth(int k)
{
int now=rt;
while(1)
{
if(t[now].s[0]&&k<=t[t[now].s[0]].siz) now=t[now].s[0];
else
{
k-=t[t[now].s[0]].siz+t[now].cnt;
if(k<=0) {splay(now);return t[now].w;}
now=t[now].s[1];
}
}
}
int pre()
{
int now=t[rt].s[0];
if(!now) return now;
while(t[now].s[1]) now=t[now].s[1];
splay(now);return t[now].w;
}
int nxt()
{
int now=t[rt].s[1];
if(!now) return now;
while(t[now].s[0]) now=t[now].s[0];
splay(now);return t[now].w;
}
void del(int k)
{
rnk(k);int now=rt;
if(t[now].cnt>1) {t[now].cnt--;getsiz(now);return;}
if(!t[now].s[0]&&!t[now].s[1]) {rt=0;clear(now);return;}
if(!t[now].s[0]) {rt=t[now].s[1];t[t[now].s[1]].fa=0;clear(now);return;}
if(!t[now].s[1]) {rt=t[now].s[0];t[t[now].s[0]].fa=0;clear(now);return;}
int x=pre();
t[t[now].s[1]].fa=rt;t[rt].s[1]=t[now].s[1];
clear(now);getsiz(rt);
}
int n;
int main()
{
scanf("%d",&n);
for(int i=1,op,x;i<=n;i++)
{
scanf("%d%d",&op,&x);
if(op==1) insert(x);
if(op==2) del(x);
if(op==3) cout<<rnk(x)<<endl;
if(op==4) cout<<kth(x)<<endl;
if(op==5) insert(x),cout<<pre()<<endl,del(x);
if(op==6) insert(x),cout<<nxt()<<endl,del(x);
}
return 0;
}
Splay 的序列操作
除了维护序列里有哪些值以外,平衡树另一个重要的用途是维护某些 只关心每个位置上的值,但是不关心大小关系 的序列。比如 lg P3391 【模板】文艺平衡树。
题意简述:给定一个长度为 的序列,支持多次区间翻转,求最后的序列。
Splay 在维护序列操作时的定义
感觉并不太好理解,当然更可能是我脑袋不好用又没看到有人讲,一直在试图把它往之前的 Splay 上类比。
这里,我们不再关心不同点的点值大小之间的关系,只关心每个权值之间的位置关系。所以这棵 Splay 虽然依旧叫 Splay,但和上文的二叉搜索树并不一样。
也就是说它现在不用满足 左子树权值 比 小一类的限制,它就是一棵正常的二叉树,中序遍历这棵树得到的权值序列是题里要维护的序列。或者说,满足二叉搜索树性质的是点的下标,而不再是权值。
比如序列 ,它对应的 Splay 就可以长成这样子:
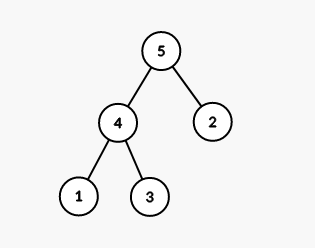
Splay 函数的改进
虽然这棵 Splay 已经不满足二叉搜索树的性质,但 rotate 函数旋转后不改变树的中序遍历,这一点是没变的。所以还是可以用原来的 Splay 函数来操作这棵树。
那为什么要改进呢?要先知道,我们想怎么维护区间翻转。
考虑对上图的一整个序列都区间翻转,看看对应的 Splay 有什么变化:
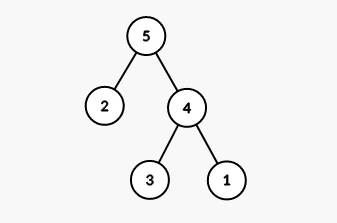
发现其实本质是交换这棵树内每个节点的左右儿子。所以考虑使用类似线段树的 lazy 标记,在这个点打标记,表示 pushdown 时要交换它的两个子树。
也要注意,给 打标记的时候 这个点的左右儿子还没换,这与线段树的 lazytag 不同。线段树在 上打标记,表示 已经修改过了,将要修改儿子的贡献。
当然你把它定义成和线段树一样的也不是不行,我很长一段时间里都这么写。但这样写 corner case 巨大多,看题解代码又一头雾水。后来才知道是定义不同上出的锅,衷心祝愿大家不要再踩雷。
这么做的前提,是要修改的区间正好在同一个子树里。对于不在一个子树里的情况,我们想点办法把它们转到一起。
更改 splay 函数的定义。我们令 splay(x,y) 表示 把下标为 的点一路向上转,直到它成为 的某个儿子。那么,假设我们现在想让下标为 的在一个子树里。
下文的图中,点的编号表示的是下标,不是权值。 显然,下标的中序遍历一定是 。
我们先 splay(l-1,0),把 转到根上(图可能有点抽象,但是不赶工今天上午都写不完了):
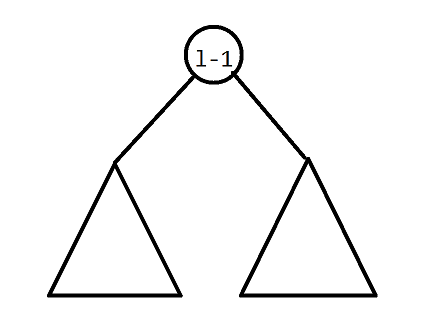
那么 肯定在根的右子树里,再 splay(r+1,l-1),把 转到 的下面。
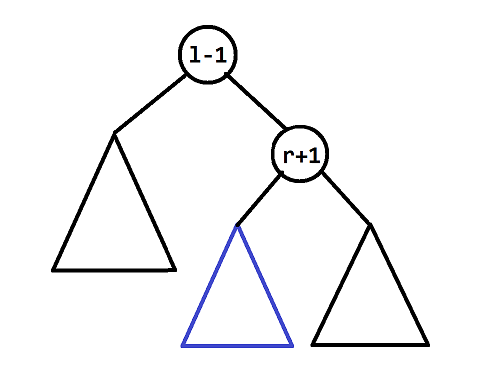
可以看出来,蓝色的那个子树就是区间 。
为了处理翻转 找不到 和 的问题,我们在 号点前和 号点后各插入一个虚点,用于翻转区间。这两个点权值是啥不重要,但是要能根据权值区分出来谁是虚点(因为它们不能输出),这里就赋成 了。
改进后的 Splay 函数,其实就是把判断父亲是不是根改成判断是不是 。
void splay(int x,int y)
{
for(int f=fa(x);f=fa(x),f!=y;rotate(x))
if(fa(f)!=y) rotate(get(f)==get(x)?f:x);
if(!y) rt=x;
}
其他函数
Find
使用 find 函数找到下标为 的点,原理和二叉搜索树的 kth 函数相同。中间要记得一边找一边 pushdown。同时因为有虚点,所以排名是实际的下标 。
il int find(int x)
{
int now=rt; x++;
while(now)
{
pushdown(now); int sz=tr[ls(now)].siz+1;
if(sz==x) break;
else if(sz>x) now=ls(now);
else now=rs(now),x-=sz;
}
return now;
}
reverse
根据上面的图,reverse 函数也不难写出:
il void reverse(int l,int r)
{
int x=find(l-1); splay(x,0);
int y=find(r+1); splay(y,x);
tr[ls(y)].lz^=1;
}
懒喵式建树!
建树的方法很多,比如像二叉搜索树一样写 insert 函数 / 类似于线段树的递归式建树。
但是樱雪喵比较懒,就直接一个循环把树建成一条链了,反正后面也要 splay 的。
il void build()
{
rt=newnode(0); int now=rt;
for(int i=1;i<=n+1;i++,now=rs(now)) tr[now].siz=n+3-i,rs(now)=newnode(a[i]),fa(rs(now))=now;
}
输出
中序遍历并输出就好了,别忘 pushdown,注意判一下虚点不输出。
void write(int now)
{
pushdown(now);
if(ls(now)) write(ls(now));
if(tr[now].key) printf("%d ",tr[now].key);
if(rs(now)) write(rs(now));
}
至此,用 Splay 维护序列的基本操作就完成了。贴一个本题的完整代码:
点击查看代码
#include<bits/stdc++.h>
#define il inline
using namespace std;
il int read()
{
int xr=0,F=1; char cr;
while(cr=getchar(),cr<'0'||cr>'9') if(cr=='-') F=-1;
while(cr>='0'&&cr<='9')
xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
return xr*F;
}
const int N=1e5+5,inf=2e9;
struct tree
{
int s[2],siz,fa,key,lz;
tree(){s[0]=s[1]=siz=fa=key=lz=0;}
}tr[N];
#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa
int rt,idx,a[N];
il int newnode(int key) {tr[++idx].key=key,tr[idx].siz=1;return idx;}
il void maintain(int x) {tr[x].siz=tr[ls(x)].siz+tr[rs(x)].siz+1;}
il void clear(int x) {ls(x)=rs(x)=fa(x)=tr[x].siz=tr[x].key=0;}
il bool get(int x) {return x==rs(fa(x));}
il void rotate(int x)
{
int y=fa(x),z=fa(y); int c=get(x);
if(tr[x].s[c^1]) fa(tr[x].s[c^1])=y;
tr[y].s[c]=tr[x].s[c^1],tr[x].s[c^1]=y,fa(y)=x,fa(x)=z;
if(z) tr[z].s[y==tr[z].s[1]]=x; //not get(y)!
maintain(y),maintain(x);
}
il void splay(int x,int y)
{
for(int f=fa(x);f=fa(x),f!=y;rotate(x))
if(fa(f)!=y) rotate(get(f)==get(x)?f:x);
if(!y) rt=x;
}
il void pushdown(int x)
{
if(!tr[x].lz) return;
swap(ls(x),rs(x)),tr[ls(x)].lz^=1,tr[rs(x)].lz^=1;
tr[x].lz=0; return;
}
il int find(int x)
{
int now=rt; x++;
while(now)
{
pushdown(now); int sz=tr[ls(now)].siz+1;
if(sz==x) break;
else if(sz>x) now=ls(now);
else now=rs(now),x-=sz;
}
return now;
}
il void reverse(int l,int r)
{
int x=find(l-1); splay(x,0);
int y=find(r+1); splay(y,x);
tr[ls(y)].lz^=1;
}
void write(int now)
{
pushdown(now);
if(ls(now)) write(ls(now));
if(tr[now].key) printf("%d ",tr[now].key);
if(rs(now)) write(rs(now));
}
int n,m;
il void build()
{
rt=newnode(0); int now=rt;
for(int i=1;i<=n+1;i++)
tr[now].siz=n+3-i,rs(now)=newnode(a[i]),fa(rs(now))=now,now=rs(now);
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=i;
rt=newnode(0); int now=rt;
for(int i=1;i<=n+1;i++) tr[now].siz=n+3-i,rs(now)=newnode(a[i]),fa(rs(now))=now,now=rs(now);
while(m--)
{
int l=read(),r=read();
reverse(l,r);
}
write(rt);
return 0;
}
更复杂的序列操作
在节点里添加更多信息,就可以维护一些更复杂的东西。比如这个经典题 P2042 [NOI2005] 维护数列。这里不具体讲做法了,很阴间,建议写之前做好调一天的心理准备。
算是写完了吧?为了补 ybtoj 而学 LCT,但是用了一上午写了一篇 Splay,怎么回事呢。至少在打字速度上取得了进步,倒也不坏。
LCT 的学习笔记没准下午写?要是学不会就学会了再写(
那就完结撒花!ww
本文来自博客园,作者:樱雪喵,转载请注明原文链接:https://www.cnblogs.com/ying-xue/p/17122409.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律