点分治详解【2023.9 重构】

2023.9 upd. 修了一下。
原文交了学校的研究性学习，反正可以糊弄老师看不懂（雾）。

虽然点分治过程本质相同，但同一个问题统计答案的方式很多。比如 luogu 点分治板子，题解区主要有三种做法：

• 开两个桶区分是否在当前子树，统计答案（本文的原做法）
• 按 \(dis\) 排序，双指针找合法区间
• 不考虑相同子树问题，先用桶处理答案再容斥

下文对三种做法分别进行说明，有事实性错误麻烦指出。

---

尽量正着说。

引入

点分治是一个快速处理树上问题的好方法。
这里的「树上问题」，指使用点分治的前提条件是我们不那么关心树的具体形态，比如 路径、连通块 相关的问题。
你可能会觉得它们明明很关心树的形态，不过别急。

这里先挂出一道例题，让大家对点分治能处理的问题有一个初步的认知，下文的讲解全部以该题为例。
lg P3806 【模板】点分治1
题意：给定一棵有 \(n\) 个点的树，询问树上距离为 \(k\) 的点对是否存在。

我们先考虑高级一点的暴力怎么做。
一个基本的暴力是枚举每个点对 \((u,v)\)，再树剖/倍增求它们的 LCA，时间复杂度 \(O(n^2\log n)\)。
在这个暴力的基础上看起来没有什么优化空间，那我们尝试先枚举 \(LCA\)。
指定根节点为 \(1\)。对于每个点 \(u\)，我们统计 所有以点 \(u\) 为 LCA 的点对 对答案的贡献。对此，我们可以开一个桶存放每个子树里出现的 \(dis\) 值，统计点 \(u\) 的时间复杂度为 \(O(siz_u)\)，总的时间复杂度即为 \(O(\sum siz_i)\)。
如果你不理解这个暴力，可以参照下面的代码：

void getdis(int now,int fa)//处理子树里每个点到 now 的距离 
{
	rem[++tot]=dis[now];//把所有出现过的 dis 值塞进数组备用 
	for(int i=head[now];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa) continue;
		dis[v]=dis[now]+e[i].w,getdis(v,now);
	}
}
void calc(int now)//统计 LCA 为 now 的点对的贡献 
{
	int p=0;//记录桶里哪些数值被修改过，保证清空桶的复杂度也为 siz[now] 
	for(int i=head[now];i;i=e[i].nxt)
	{
		int v=e[i].to;if(v==fa[now]) continue;
		dis[v]=e[i].w;tot=0;
		getdis(v,now);
		for(int j=1;j<=tot;j++)
			for(int k=1;k<=m;k++)//q[k]表示第 k 次询问 
				if(q[k]>=rem[j]) flag[k]|=t[q[k]-rem[j]];
		for(int j=1;j<=tot;j++) 
			if(rem[j]<=1e7) qwq[++p]=rem[j],t[rem[j]]=1; 
	}
	for(int i=1;i<=p;i++) t[qwq[i]]=0;
}

这个做法的时间复杂度似乎依旧看不出什么优化空间，但我们不妨试试换一种统计时间复杂度的方式。
对于点 \(u\) 到根节点的路径上的每个点，统计答案都会将 \(u\) 加进桶一次，点 \(u\) 被计算的次数即为 \(dep_u\)，总的时间复杂度为 \(O(\sum dep_i)\)。
当树为一条链时，时间复杂度可以卡满，达到 \(O(n^2)\)。
想最小化 \(\sum dep_i\)，我们要做的就是在这个做法的基础上想办法降低树的高度，而这就是点分治要做的事。

前置知识-树的重心

• 定义：对于树上的每一个点，计算其所有子树中最大的子树节点数，这个值最小的点就是这棵树的重心。

由此，我们可以得出重心的性质：以树的重心为根时，所有子树的大小都不超过整棵树大小的一半。
至于怎么找重心，上述定义和性质看起来等价，似乎根据哪个来判断对结果并没有影响。
但在点分治的过程中，我们钦定使用定义来判断；这样做的原因会在后文提到。

点分治

知道了上面这些，就可以开始讲点分治的具体过程了。

考虑下图的这棵树，假设我们处理完了点 \(2,4\)，现在要处理以 \(3\) 为根的子树。

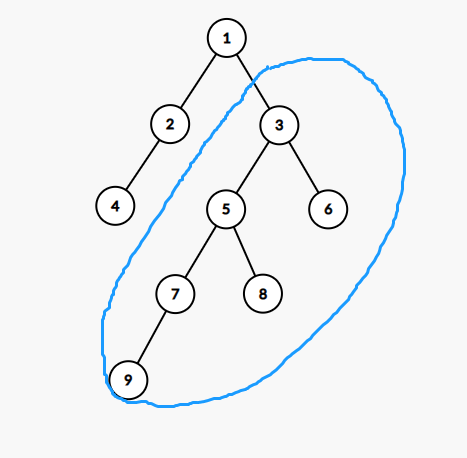
思考一个问题：处理这个子树就一定要从 \(3\) 开始处理吗？
首先可以肯定的是处理这个子树里的任何一个点都与子树外的点无关，更与 \(1\rightarrow 3\) 这条边无关。因为伸到子树外面去的路径应该在处理这棵子树前就被统计了。
所以处理到这棵子树时可以把这棵子树单独拿出来看。就像整棵树的那个根节点可以随意指定且不影响答案一样，以子树内任何一个点为根去递归处理整个子树，得到的结果是一样的。
这里选择的“根节点”与整棵子树在原图上的“根节点”是无关的，只是改变了处理答案的顺序，并没有改变原树的形态。

对于根节点的选择，前面树的重心的性质就有用了。如果选择子树的重心继续递归，这棵子树的树高一定不超过 \(O(\frac{siz_u}{2})\)。
那么每次的树高都减半的话，递归层数不会超过 \(\log_2 n\)，点分治 \(O(n\log n)\) 的复杂度就得到了保证。

（补充一句，其实点分治没有改变原树的树高，但通过改变递归顺序减少了递归层数，其实也就等同于降低了树的高度。）
这句话也有另一种理解，类比之前的 LCA。
发现要统计点对 \((x,y)\) 的答案，我们只关心能否在 \(x\to y\) 的路径上找到一个点 \(z\)，并分别统计 \(x\to z,z\to y\) 的信息。我们既不关心它们的 LCA 究竟是哪个点，也不关心 \(x\to z\) 的路径具体是什么。点分治改变树根的正确性即基于这一点，同样这也是前文所说该问题 不关心树的具体形态 的原因。

还有一个细节问题就是换了根节点之后怎么保证不会走到子树外面。
因为是从上往下处理的，处理到点 \(u\) 这棵子树的时候它的父亲一定被处理过了。那么开一个 \(vis\) 数组，每处理一个点就把它的 \(vis\) 标成 \(1\)，dfs 的时候只走 \(vis=0\) 的点就好了。

至此，点分治的部分就讲完了，梳理一下流程：

• 找当前子树的重心 (find)
• 统计 以重心为根时 以重心为 LCA 的点对 的贡献 (calc)
• 以重心为根，递归处理它的子树 (solve)

最后贴一下点分治的代码，getdis 函数和 calc 函数和上面那份暴力代码几乎相同，注释就不写了。

点击查看代码 qwq

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
	int xr=0,F=1;char cr=getchar();
	while(cr<'0'||cr>'9') {if(cr=='-') F=-1;cr=getchar();}
	while(cr>='0'&&cr<='9')
	    xr=(xr<<3)+(xr<<1)+(cr^48),cr=getchar();
	return xr*F;
}
const int N=1e4+5,M=1e7+5;
int n,m,Q[N];
struct edge{
	int nxt,to,w;
}e[N<<1];
int head[N],cnt;
void add(int u,int v,int w){
	e[++cnt]={head[u],v,w};head[u]=cnt;
}
int dis[N],rem[N],tot;
int t[M],ans[N],vis[N],siz[N],mx[N],S,rt;
void find(int now,int fa)
{
	siz[now]=1,mx[now]=0;
	for(int i=head[now];i;i=e[i].nxt)
	{
		int v=e[i].to; 
		if(vis[v]||v==fa) continue;
		find(v,now);
		siz[now]+=siz[v],mx[now]=max(mx[now],siz[v]);
	}
	mx[now]=max(mx[now],S-siz[now]);
	if(mx[now]<mx[rt]) rt=now;
}
void getdis(int now,int fa)
{
	rem[++tot]=dis[now]; 
	for(int i=head[now];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(vis[v]||v==fa) continue;
		dis[v]=dis[now]+e[i].w;
		getdis(v,now);
	}
}
int tsh[N],qwq;
void calc(int now)
{
	qwq=0;t[0]=1;
	for(int i=head[now];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(vis[v]) continue;
		dis[v]=e[i].w,tot=0,getdis(v,now);
		for(int j=1;j<=tot;j++)
			for(int k=1;k<=m;k++)
				if(Q[k]>=rem[j]&&t[Q[k]-rem[j]]) ans[k]=1;
		for(int j=1;j<=tot;j++) if(rem[j]<=1e7) t[rem[j]]=1,tsh[++qwq]=rem[j];
	}
	while(qwq) t[tsh[qwq--]]=0;
}
void solve(int now)
{
	vis[now]=1,calc(now);
	for(int i=head[now];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(vis[v]) continue;
		find(v,now),S=siz[v],rt=0,mx[0]=1e9;
		find(v,now);
		solve(rt);
	}
}
int main()
{
	n=read(),m=read();
	for(int i=1;i<n;i++)
	{
		int u=read(),v=read(),w=read();
		add(u,v,w),add(v,u,w);
	}
	S=n;
	for(int i=1;i<=m;i++) Q[i]=read();
	solve(1);
	for(int i=1;i<=m;i++) printf(ans[i]?"AYE\n":"NAY\n");
	return 0;
}

calc 函数的其他写法

不论具体的题目是什么，点分治的过程都是不变的，区别在于对特定的点统计经过它的路径的 calc 函数。
依旧以上题为例，也有其他统计答案的方法。这里写两个比较常见的，它们对做其他题目的思路或许会有一些启发作用。

双指针

不依赖于询问值域的做法，但复杂度是 \(O(n\log^2 n+nm\log n)\)。这个多出来的排序 \(\log\) 似乎不在瓶颈上？

\(\text{calc}(u)\) 时，我们 dfs 预处理子树内的每个点。\(dis_i\) 表示点 \(i\) 到 \(u\) 的距离，\(bel_i\) 表示 \(i\) 属于 \(u\) 的哪棵子树。同时，用 \(t\) 数组保存子树内所有点的编号。
把 \(t\) 数组内的点按 \(dis\) 值升序排序。
那么我们要找 \(dis_x+dis_y=k\) 且 \(bel_x\neq bel_y\) 的点对。定义双指针 \(l,r\)，易知在 \(l\) 增加的过程中 \(r\) 一定变小。
于是分成四种情况：

• \(dis_{t_l}+dis_{t_r}>k\)，左移 \(r\)；
• \(dis_{t_l}+dis_{t_r}<k\)，右移 \(l\)；
• \(dis_{t_l}+dis_{t_r}<k\)，但在同一棵子树，左移 \(r\)；（这里原题解分了两种情况讨论，但没有必要，实测统一左移 \(r\) 没有问题）
• 都不满足，说明 \(dis\) 和等于 \(k\) 且不在一棵子树。那么这条路径合法，累加答案。

只需要把 calc 函数改一下。

il bool cmp(int x,int y) {return dis[x]<dis[y];}
il void calc(int u)
{
    tot=0; t[++tot]=u,bel[u]=u,dis[u]=0;
    for(int i=head[u];i;i=e[i].nxt)
    {
        int v=e[i].to,w=e[i].w;
        if(vis[v]) continue;
        getdis(v,u,v,w);
    }
    sort(t+1,t+tot+1,cmp);
    for(int i=1;i<=m;i++)
    {
        if(ans[i]) continue;
        int l=1,r=tot;
        while(l<r)
        {
            if(dis[t[l]]+dis[t[r]]>q[i]) r--;
            else if(dis[t[l]]+dis[t[r]]<q[i]) l++;
            else if(bel[t[l]]==bel[t[r]]) r--;
            else {ans[i]=1;break;}
        }
    }
}

容斥

很普遍，但是没找到复杂度正确的容斥写法的 blog。
大致思想是，我们不考虑是否在同一子树，两两枚举 \(u\) 内的点，再容斥掉同一子树的贡献。两两枚举这步会被菊花图卡成 \(O(n^2)\)。

不同找重心方法的时间复杂度分析

其实对于上文代码的写法，使用哪种找重心都可以。
但有很多人的 solve 是这么写：

void solve(int now)
{
	vis[now]=1,calc(now);
	for(int i=head[now];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(vis[v]) continue;
		S=siz[v],rt=0,mx[0]=1e9;
		find(v,now);
		solve(rt);
	}
}

这里传入的 \(S\) 值并不是实际的 \(siz_v\)，看起来并不正确。实际上这种写法的正确性取决于找重心的方式，找 \(n/2\) 的确实不对，但找最小子树是对的。
具体的证明可以看 lca-一种基于错误的寻找重心方法的点分治的复杂度分析。

看起来就这些，点分树学会了再写。
done update.