网络流 24 题做题记录

网上似乎找不到关于网络流24题顺序的博客...那就按 lg 难度标签随机开题力（）
昨天划水一天只学了 EK 和 Dinic，希望够用（？
感觉写博客在加深印象这方面的效果还是相当不错的qwq

最大流

P2763 试题库问题

自己完全看不出和网络流有啥关系...看完题解只能说是长见识了qwq
对于匹配问题，先建立源点汇点，源点与题目相连，边权为 1；汇点与类型相连，边权为该类型的题目数。
然后对于每道题向它属于的类型连边，边权为 1。
借用一张洛谷题解里的图 \(\downarrow\)

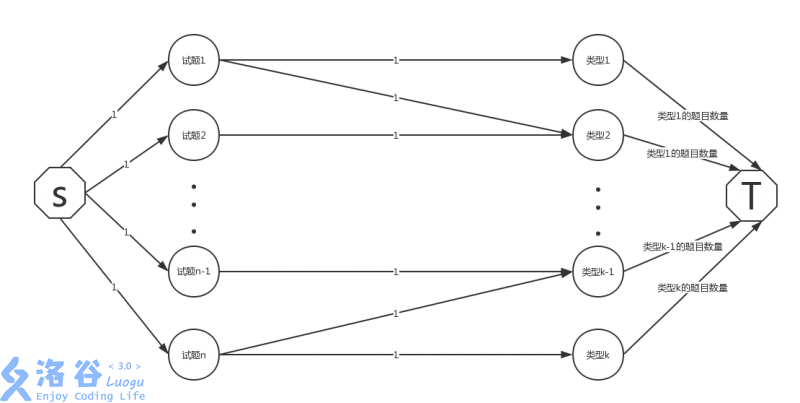
至于统计方案，对于右面类型节点，遍历他们相邻节点（除 t 以外）有哪些边权为 \(1\) 即可。（反边边权为 1，证明这条路被走过）

P3254 圆桌问题

和上一题异曲同工诶qwq
源点向每个公司连边，容量为公司人数；每个桌子向汇点连边，容量为桌子能容纳的人数。然后每个公司分别向每个桌子连一条容量为 1 的边，跑最大流。

P2756 飞行员配对方案问题

二分图匹配板子（？ 最简单的一题qwq
连边和上面一样，所有边权都是 \(1\)。没了。

P2764 最小路径覆盖问题

真的看了好久才理解为什么是二分图/kk
因为原图是 DAG，所以链的数量就是匹配不上的边的数量。（每断开一条边都多出一条链）
每个点最多只有一个入度一个出度。所以可以把点拆开考虑连向它的点和它连向的点。保证都最多有一个就行。
那对于原图每条边 (u,v)，在新图上就是 (u,v+n,1)。跑最大流进行匹配即得答案。

P2765 魔术球问题

基本和上题同理。
把每个点拆成两个，因为从小往大放，对于每个点和比它小且和为完全平方数的点连边。
每加一个点跑一遍最大流，需要的柱子数就是球数-匹配数。
注意：判断完全平方数千万不要写 return sqrt(x)*sqrt(x)==x ，你会喜提本机 AC 洛谷 RE！（调了我 1h/fn
p.s.正确写法：return (int)sqrt(x)*sqrt(x)==x

最小割

P3355 骑士共存问题

不会，打开题解，题解让我先去做方格取数，等我做完回来填坑/kel
题面都给画出红黄格子了，那就和方格取数一样分成两部分做。然后两边容量都是 1，中间是 inf。基本是一个东西，连边方法改改就行。

P2774 方格取数问题

寄。最小割没学。学完再写（？ upd:好了学完了，回来写题解了qwq
先把所有方格分成黑点和白点。（说不明白，像国际象棋棋盘那么分（？）
然后合法解就是要满足没有相邻的黑点白点被同时选。
源点向所有黑点连边，容量为点权；同理，所有白点向汇点连边。然后对于每个黑点向与它相邻的白点连容量为 inf 的边。
合法解则为选择容量尽可能小的边删除，使得源点不能到达汇点，即最小割。
由于最小割=最大流，对这个图跑最大流，最后答案就是 \(sum-ans\)。

费用流

P4014 分配问题

源点向每个人连边，每件工作向汇点连边，容量为 \(1\)，费用为 \(0\)；人向工作连边，容量为 \(1\)，费用为 \(c_{i,j}\)。
分别 spfa 找最短路最长路。

P4015 运输问题

怎么这么多板子...
源点向每个仓库连边，容量为 \(a_i\)；每个商店向汇点连边，容量为 \(b_i\)。费用都是 \(0\)。
仓库向商店连边，容量无限制(inf)，费用为 \(c_{i,j}\)。在图上跑费用流。

P4013 数字梯形问题

码农题能不能去似啊/fn
对于权值在点上不好处理，我们把一个点拆成两个，点权就是连接这两个新点的边权。
第一问：所有边容量都是 \(1\)。
第二问：连接不同层的边容量为 \(1\)，连接一个点所拆出不同点的边容量为 \(2\)。
第三问：所有边（源点到第一层除外）容量为 inf。
分别建图并跑费用流。

P4016 负载平衡问题

懒得写网络流做法（
如果是一个链而不是环，可以直接贪心，优先满足左边。
而环的情况下一定有两堆之间没有移动。枚举这个断点并贪心找最小答案即可。

P3358 最长k可重区间集问题

一道建了不知道多少个假图的坑人题。终于过了。
说不明白，看图 \(\downarrow\) （样例）

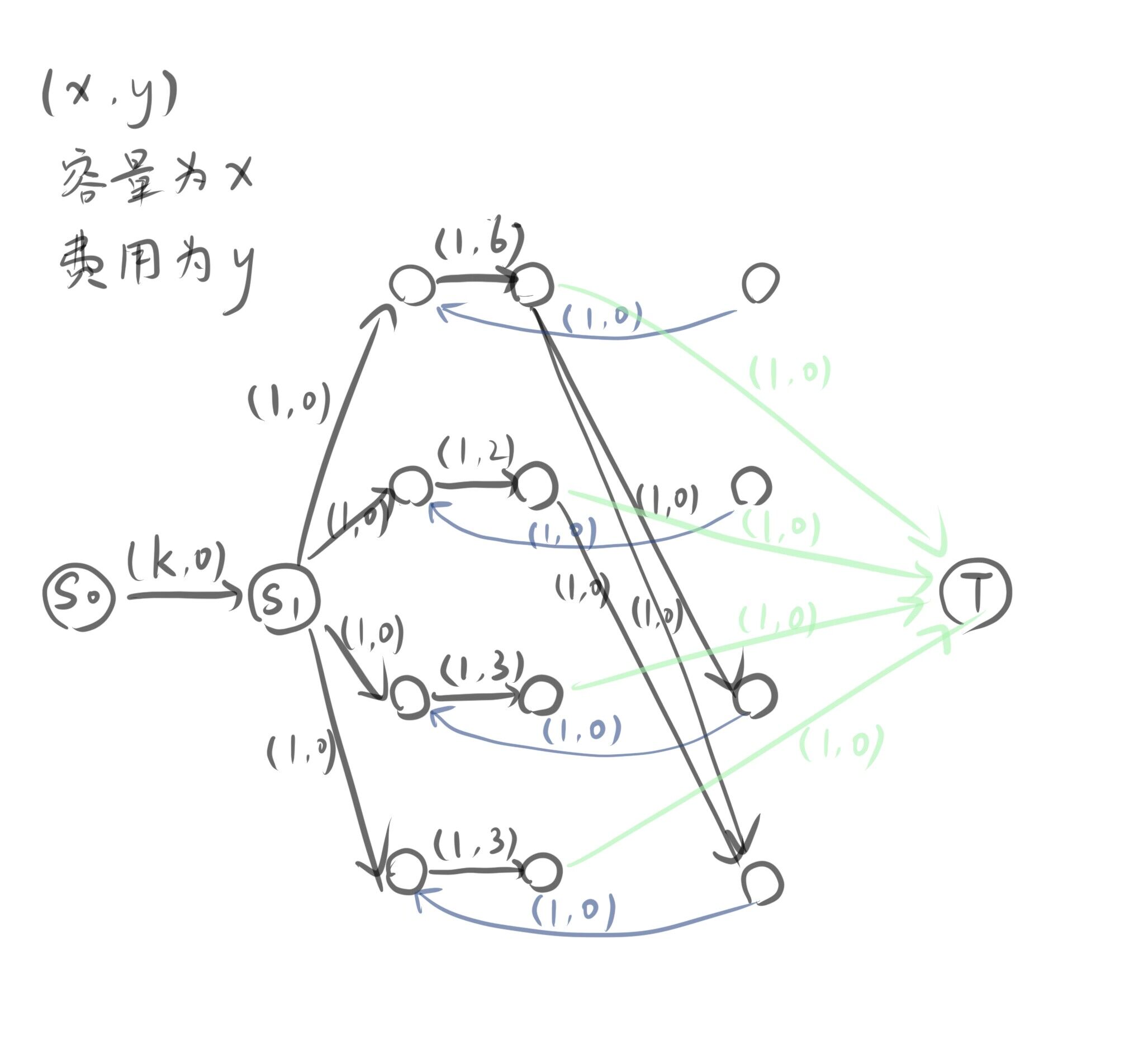
虽然我自己看着都不靠谱，但确实是对的（？
注意区间 (l,r) 的长度是 r-l 而不是 r-l+1。

附：

建议开题顺序

（同一类型题难度从小到大排列）

最大流

• 飞行员配对方案问题
• 试题库问题
• 圆桌问题
• 最小路径覆盖问题
• 魔术球问题

最小割

• 方格取数问题
• 骑士共存问题

费用流

• 负载平衡问题
• 分配问题
• 运输问题
• 数字梯形问题
• 最长k可重区间集问题

p.s. 现在处于 打开一道题->思考->想不出来->换一道题 的状态（？
最后还是决定先去学别的了。咕咕咕。