HDU 1025 LIS二分优化

题目链接：

acm.hdu.edu.cn/showproblem.php?pid=1025

Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 28755    Accepted Submission(s): 8149

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.



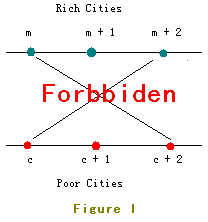
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

 

 

Output

For each test case, output the result in the form of sample.
You should tell JGShining what's the maximal number of road(s) can be built.

 

 

Sample Input

2

1 2

2 1

3

1 2

2 3

3 1

 

 

Sample Output

Case 1:

My king, at most 1 road can be built.

 

Case 2:

My king, at most 2 roads can be built.

Hint

Huge input, scanf is recommended.

 

题目大意就是给出两两配对的poor city和rich city，求解最多能修几条不相交的路。此题可以转化为LIS问题。转化过程如下：

数据中有2列，为方便表述，暂且叫做第一列和第二列。
1.若第一列是是递增的（给出的2个样例都是递增的），那么要想尽可能多的做连线，则那么就需要找出第二列中最长的递增子序列，若出现非递增的序列，那么连线后一定会相交。
2.若第一列不是递增的，排序后按照1分析即可。
综上所述，题目便转换成LIS问题。

LIS有2种写法，一种是o(n²)的写法，一种是o(nlogn)的写法。题目中给出n<=500,500.采用o(n²）必定超时，最佳策略是o(nlogn)。
推荐一篇介绍这种写法的博文
最长上升子序列nlogn算法。通俗易懂，在此就不赘述如何设计此算法了。

 

 

LIS问题，不过要优化

#include<bits/stdc++.h>
#define max_v 500005
using namespace std;
int a[max_v],dp[max_v],len;
int main()
{
    int n,c=1;
    while(~scanf("%d",&n))
    {
        for(int i=1; i<=n; i++)
        {
            int x,y;
            scanf("%d %d",&x,&y);
            a[x]=y;
        }
        //dp[k]代表长度为k的LIS序列的最末元素,
        //若有多个长度为k的上升子序列，
        //则记录最小的那个最末元素
        //dp[]中的元素是单调递增的，
        //二分优化的时候利用这个性质

        dp[1]=a[1];
        len=1;
        for(int i=2; i<=n; i++)
        {
            if(a[i]>dp[len])
            {
                dp[++len]=a[i];
            }
            else
            {
               int j=lower_bound(dp,dp+len,a[i])-dp;
                dp[j]=a[i];
            }
        }
        if(len==1)
        {
            printf("Case %d:\nMy king, at most %d road can be built.\n\n",c++,len);
        }else
        {
            printf("Case %d:\nMy king, at most %d roads can be built.\n\n",c++,len);
        }
    }
    return 0;
}