洛谷4719 【模板】动态dp 学习笔记(ddp 动态dp)
qwq大概是混乱的一个题。
首先,还是从一个比较基础的想法开始想起。
如果每次暴力修改的话,那么每次就可以暴力树形dp
令\(dp[x][0/1]\)表示\(x\)的子树中,是否选择\(x\)这个点的最大权独立集。
如果这个点不选,那么他的所有儿子都是可以选的。
如果这个点选的,那么只能加上他的所有儿子不选的收益。
因为收益可能存在负数,所以要特别处理一下
void dfs(int x,int fa)
{
f[x][0]=0;
f[x][1]=val[x];
for (int i=point[x];i;i=nxt[i])
{
int p = to[i];
if (p==fa) continue;
dfs(p,x);
f[x][0]=max(f[x][0],f[x][0]+max(f[p][1],f[p][0]));
f[x][1]=max(f[x][1],f[x][1]+f[p][0]);
}
}
那么暴力修改的版本就迎刃而解了。
但是如何做正常的修改呢?
这时候就需要一个黑科技了
动态dp
动态dp大致上的思路就是通过矩阵来实现dp的转移,从而能做到快速修改的效果。
那么回到这个题。
由于是树上,所以不难相当用树链剖分+线段树来求解问题
由于刚才那个\(dp\)状态不太好优化,我们不妨来定义一下新的状态。
我们令\(dp[i][0/1]\)表示\(i\)的子树内,不考虑\(i\)的重儿子的是否选\(i\)的最大独立集。
然后用\(dp1\)表示上文的\(dp\)状态。
那么通过两遍\(dfs\)确定轻重儿子和相关信息之后,其实两个数组也就比较好处理了。
void solve(int x,int fa) //这里dp数组是忽略重儿子的贡献,dp1则是原来的dp,不能开成一个数组的原因是因为那样就不能保证一个点只会有重儿子被忽略
{
dp[x][0]=0;
dp[x][1]=val[x];
dp1[x][0]=0;
dp1[x][1]=val[x];
for (int i=point[x];i;i=nxt[i])
{
int p = to[i];
if (p==fa) continue;
solve(p,x);
dp1[x][0]=max(dp1[x][0],dp1[x][0]+max(dp1[p][0],dp1[p][1]));
dp1[x][1]=max(dp1[x][1],dp1[x][1]+dp1[p][0]);
if (p!=son[x])
{
dp[x][0]=max(dp[x][0],dp[x][0]+max(dp1[p][0],dp1[p][1]));
dp[x][1]=max(dp[x][1],dp[x][1]+dp1[p][0]);
}
}
}
需要注意的是,我们的\(dp\)数组,只是忽略当前子树的重儿子。qwq所以处理的时候,要用\(dp1\)更新\(dp\)。
但是其实到现在,对这个题还是没什么进展。
现在考虑怎么用这个\(dp\)数组来算答案呢。
我们令\(f\)表示现在的\(dp\),然后用\(g\)表示最终的\(ans\)。
那么不难发现$$g[i][0]=f[i][0]+max(g[son[i]][0/1])$$
如果我们定义一种新的矩阵运算\(max\),表示\(c[i][j]=max(c[i][j],a[i][k]+b[k][j])\)
那么实际上我们可以通过一个矩阵来完成转移?
没错
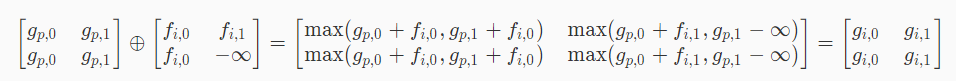
观察不难发现,对于每一个点的转移矩阵,其实就是那个\(f\)的矩阵,因为这个是可以实现就预处理好的。
那么由于对于一条重链来说,链尾的元素的\(g\)与\(f\)是相等的,并且矩阵乘法具有结合律,所以我们可以直接通过预处理某一个点,到他所在重链的链尾的区间矩阵乘积的和来求出这个点的\(g\),实际上每次询问答案,只需要查询1的值即可。
那么现在的问题就剩下怎么修改了
其实上面的转移过程,主要是为了修改做准备。
首先修改的时候,会修改这个单点的矩阵的值。
然后依次会修改每一条重链的链头\(fa\)的转移矩阵(相当于每一条重链的链头会发生变化,而他相对于他的父亲又是轻儿子,所以会影响)
这里修改的时候,我们选择一个策略就是用他原来的贡献,减去他现在的贡献。
所以要记录一个\(pre\)数组表示这个点的转移矩阵是什么,然后每次计算起来就比较方便,总之还是细节比较多的。
qwqqqqq
直接看代码吧
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<map>
#include<set>
#define pb push_back
#define mk make_pair
#define ll long long
#define lson ch[x][0]
#define rson ch[x][1]
#define int long long
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while (!isdigit(ch)) {if (ch=='-') f=-1;ch=getchar();}
while (isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
const int maxn = 1e6+1e2;
const int maxm = 2*maxn;
const int inf = -1e9;
struct Ju{
int x,y;
int a[3][3];
Ju operator * (Ju b)
{
Ju ans;
ans.x=x;
ans.y=b.y;
for (int i=1;i<=ans.x;i++)
for (int j=1;j<=ans.y;j++)
ans.a[i][j]=inf;
for (int i=1;i<=ans.x;i++)
for (int j=1;j<=ans.y;j++)
for (int k=1;k<=y;k++)
ans.a[i][j]=max(ans.a[i][j],a[i][k]+b.a[k][j]);
return ans;
}
};
void print(Ju x)
{
cout<<x.x<<" "<<x.y<<endl;
for (int i=1;i<=2;i++)
{
for (int j=1;j<=2;j++) cout<<x.a[i][j]<<" ";
cout<<endl;
}
cout<<"----------------"<<endl;
}
int point[maxn],nxt[maxm],to[maxm];
Ju f[4*maxn];
int dp[maxn][2];
int cnt,n,m,newnum[maxn];
Ju pre[maxn]; //pre表示之前的矩阵是多少,这个便于计算贡献。
int dfn[maxn],top[maxn],fa[maxn],tail[maxn];
int son[maxn],size[maxn];
int tot,q,val[maxn];
int back[maxn];
int dp1[maxn][2];
void addedge(int x,int y)
{
nxt[++cnt]=point[x];
to[cnt]=y;
point[x]=cnt;
}
//因为树上合并是从下到上,所以线段树的合并应该是右儿子乘左儿子。
void up(int root)
{
f[root]=f[2*root+1]*f[2*root];
}
void build(int root,int l,int r)
{
if (l==r)
{
f[root].x=2;
f[root].y=2;
f[root].a[1][1]=dp[back[l]][0];
f[root].a[1][2]=dp[back[l]][1];
f[root].a[2][1]=dp[back[l]][0];
f[root].a[2][2]=inf;
//pre[back[l]]=f[root];
// cout<<back[l]<<" "<<l<<" ";
// print(f[root]);
return;
}
int mid = l+r >> 1;
build(2*root,l,mid);
build(2*root+1,mid+1,r);
up(root);
}
void update(int root,int l,int r,int x,Ju p)
{
if (l==r)
{
f[root]=p;
return;
}
int mid = l+r >> 1;
if (x<=mid) update(2*root,l,mid,x,p);
if (x>mid) update(2*root+1,mid+1,r,x,p);
up(root);
}
Ju query(int root,int l,int r,int x,int y)
{
//cout<<l<<" "<<r<<" "<<x<<" "<<y<<endl;
if (x<=l && r<=y)
{
return f[root];
}
int mid = l+r >> 1;
if (y<=mid) return query(2*root,l,mid,x,y);
if (x>mid) return query(2*root+1,mid+1,r,x,y);
return query(2*root+1,mid+1,r,x,y)*query(2*root,l,mid,x,y);
}
void dfs1(int x,int faa)
{
size[x]=1;
int maxson=-1;
for (int i=point[x];i;i=nxt[i])
{
int p = to[i];
if (p==faa) continue;
dfs1(p,x);
fa[p]=x;
size[x]+=size[p];
if (size[p]>maxson)
{
maxson=size[p];
son[x]=p;
}
}
}
void dfs2(int x,int chain)
{
tail[chain]=x;
top[x]=chain;
newnum[x]=++tot;
back[tot]=x;
if (!son[x]) return;
dfs2(son[x],chain);
for (int i=point[x];i;i=nxt[i])
{
int p = to[i];
if (!newnum[p]) dfs2(p,p);
}
}
void solve(int x,int fa) //这里dp数组是忽略重儿子的贡献,dp1则是原来的dp,不能开成一个数组的原因是因为那样就不能保证一个点只会有重儿子被忽略
{
dp[x][0]=0;
dp[x][1]=val[x];
dp1[x][0]=0;
dp1[x][1]=val[x];
for (int i=point[x];i;i=nxt[i])
{
int p = to[i];
if (p==fa) continue;
solve(p,x);
dp1[x][0]=max(dp1[x][0],dp1[x][0]+max(dp1[p][0],dp1[p][1]));
dp1[x][1]=max(dp1[x][1],dp1[x][1]+dp1[p][0]);
if (p!=son[x])
{
dp[x][0]=max(dp[x][0],dp[x][0]+max(dp1[p][0],dp1[p][1]));
dp[x][1]=max(dp[x][1],dp[x][1]+dp1[p][0]);
}
}
}
void modify(int x,int y)//本质上,一次修改,就是 先单点修改, 然后依次修改每一条重链的链头的父亲(因为同一条链是可以直接乘法得到的,所以不用修改)
{
Ju tmp = query(1,1,n,newnum[x],newnum[x]);
//print(tmp);
tmp.a[1][2]+=y-val[x];
val[x]=y;
//print(tmp);
update(1,1,n,newnum[x],tmp);
for (int now=top[x];now!=1;now=top[now])
{
int faa = fa[now];
Ju ymh = query(1,1,n,newnum[faa],newnum[faa]); //当前点的父亲修改之前的值
Ju lyf = query(1,1,n,newnum[now],newnum[tail[top[now]]]); //这一段重链的值
ymh.a[1][1]+=max(lyf.a[1][1],lyf.a[1][2])-max(pre[now].a[1][1],pre[now].a[1][2]);
ymh.a[1][2]+=lyf.a[1][1]-pre[now].a[1][1];
ymh.a[2][1]=ymh.a[1][1];
update(1,1,n,newnum[faa],ymh);
pre[now]=lyf;//每次更新完他的父亲,就把pre数组修改
now=fa[now];
//cout<<now<<endl;
//print(ymh);
}
}
signed main()
{
n=read(),q=read();
for (int i=1;i<=n;i++) val[i]=read();
for (int i=1;i<n;i++)
{
int x=read(),y=read();
addedge(x,y);
addedge(y,x);
}
dfs1(1,0);
dfs2(1,1);
solve(1,0);
// for (int i=1;i<=n;i++)
// {
// cout<<i<<" "<<tail[top[i]]<<" "<<son[i]<<" "<<dp[i][0]<<" "<<dp[i][1]<<endl;
// }
build(1,1,n);
//cout<<query(1,1,n,newnum[1],newnum[tail[top[1]]]).a[1][1]<<endl;
for (int i=1;i<=n;i++)
{
pre[i]=query(1,1,n,newnum[i],newnum[tail[top[i]]]);
//print(pre[i]);
}
//return 0;
for (int i=1;i<=q;i++)
{
int x=read(),y=read();
modify(x,y);
Ju ymh = query(1,1,n,newnum[1],newnum[tail[top[1]]]);
cout<<max(ymh.a[1][1],ymh.a[1][2])<<"\n";
}
return 0;
}


