基数排序 顺序实现与链式实现
最近数据结构刚刚讲完了基数排序,以下我的一些见解:
大多数的排序都是通过比较数据大小的方法对待排数据序列进行排序整理过程。
而基数排序却很另类,那么,基数排序是采用怎样的策略进行排序的呢?
简要概括一下:基数排序是通过“分配”和“收集”两个过程来实现排序的。
而这个思想该如何理解呢?请看以下例子:
(1)有以下待排序列
309 385 867 183 341 605 385
(2)第一次分配和收集:
首先按照各个数据的个位数字(即按照9,5,7,3,1,5,5)分配到0-9的10个区间内
结果如下:

分配结束后。接下来将所有空间中的数据按照序号由小到大依次重新收集起来,得到如下仍然无序的数据序列:

(3)第二次分配和收集:
这次按照十位数字进行分配,步骤同上
结果如下:

分配结束后。接下来将所有空间中的数据按照序号由小到大依次再次收集起来,得到如下仍然无序的数据序列:

(4)第三次分配和收集:
这次按照百位数字进行分配,步骤同上
结果如下:

分配结束后。接下来将所有空间中的数据按照序号由小到大依次再次收集起来;

哎?!停一下!奇怪,数据竟然有序了!
当然,数据分别按照个,十,百位依次排序后自然是有序的,至于为什么,我相信细心的读者已经想明白了。
下面介绍一下对上面所说的基数排序算法做一些补充:
(1)如果数据大小更大,则需按照上面的思路继续排序(比如排序到千位,万位.....),排序的次数就是待排数据中最大数字的位数;
(2)上面的分析是说的数字的排序,如果要对等长的字符串集合排序,则各个空间的关键字由0-9变为‘a’-‘z’;
(3)基数排序是稳定的,而且看起来似乎在时间代价上很好,但实际并非如此,它在记录数较关键字大得多的情况下比较有效,还有一个缺点是:它对一些数据类型来说是难于实现的,如对实型或不等长的字串。
下面再思考一个问题:既然我们可以从最低位到最高位进行如此的分配收集,那么是否可以由最高位到最低位依次操作呢? 答案是完全可以的。
基于两种不同的排序顺序,我们将基数排序分为LSD(Least significant digital)或MSD(Most significant digital),
LSD的排序方式由数值的最右边(低位)开始,而MSD则相反,由数值的最左边(高位)开始。
注意一点:LSD的基数排序适用于位数少的数列,如果位数多的话,使用MSD的效率会比较好。
下面给出算法实现代码:
链式实现:

1 #include <iostream> 2 3 using namespace std; 4 const int maxn=100000+10; 5 const int Radix=20; 6 typedef struct 7 { 8 int next; 9 int key; 10 }SLNode; 11 typedef struct 12 { 13 SLNode r[maxn]; 14 int length; 15 }SLList; 16 typedef int ArrType[Radix]; 17 ArrType f,e; 18 int Ord(int k,int j) 19 { 20 for(int i=1;i<j;i++) 21 k/=10; 22 k%=10; 23 return k+10; 24 } 25 void Print_L(SLList L) 26 { 27 int mrk=0; 28 for(int p=L.r[0].next;p;p=L.r[p].next) 29 { 30 if(mrk) 31 printf(" "); 32 printf("%d",L.r[p].key); 33 mrk=1; 34 } 35 printf("\n"); 36 } 37 void Distribute(SLList &L,int i,ArrType &f,ArrType &e) 38 { 39 //printf("i=%d\n",i); 40 for(int i=0;i<Radix;i++) 41 f[i]=0; 42 //for(int p=L.r[0].next;p!=0;p=L.r[p].next) 43 for(int p=L.r[0].next;p;p=L.r[p].next) 44 { 45 int k=Ord(L.r[p].key,i); 46 //printf("%d\n",k); 47 if(f[k]==0) 48 { 49 f[k]=e[k]=p; 50 } 51 else 52 { 53 L.r[e[k]].next=p; 54 e[k]=p; 55 } 56 } 57 } 58 void Collect(SLList &L,int i,ArrType &f,ArrType &e) 59 { 60 int j=0; 61 while(f[j]==0) 62 j++; 63 L.r[0].next=f[j]; 64 int tail=e[j]; 65 while(j<Radix) 66 { 67 j++; 68 while(j<Radix&&f[j]==0) 69 j++; 70 L.r[tail].next=f[j]; 71 tail=e[j]; 72 } 73 } 74 void RadixSort(SLList &L) 75 { 76 for(int i=1;i<=6;i++)//待排数据中最大值的位数,可根据实际需要变化 77 { 78 Distribute(L,i,f,e); 79 Collect(L,i,f,e); 80 } 81 } 82 83 int main() 84 { 85 int n; 86 scanf("%d",&n); 87 SLList L; 88 L.length=n; 89 L.r[0].next=1; 90 for(int i=1;i<=n;i++) 91 { 92 scanf("%d",&L.r[i].key); 93 L.r[i].next=i+1; 94 } 95 L.r[n].next=0; 96 RadixSort(L); 97 Print_L(L); 98 return 0; 99 }
链式时间复杂度:
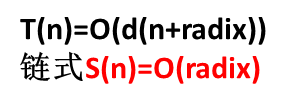
顺序实现:

1 //库函数头文件包含 2 #include<stdio.h> 3 #include<malloc.h> 4 #include<stdlib.h> 5 6 7 //函数状态码定义 8 #define TRUE 1 9 #define FALSE 0 10 #define OK 1 11 #define ERROR 0 12 #define INFEASIBLE -1 13 #define OVERFLOW -2 14 #define Radix 10 15 #define maxn 100010 16 typedef int Status; 17 typedef int QElemType; 18 19 typedef struct QNode 20 { 21 QElemType data; 22 struct QNode *next; 23 }QNode, *QueuePtr; 24 25 typedef struct 26 { 27 QueuePtr front; 28 QueuePtr rear; 29 }LinkQueue; 30 31 Status InitQueue(LinkQueue &Q) 32 { 33 Q.front=Q.rear=(QueuePtr)malloc(sizeof(QNode)); 34 if(!Q.front) 35 exit(OVERFLOW); 36 Q.front->next=NULL; 37 return OK; 38 } 39 Status DestroyQueue(LinkQueue &Q) 40 { 41 while(Q.front) 42 { 43 Q.rear=Q.front->next; 44 free(Q.front); 45 Q.front=Q.rear; 46 } 47 return OK; 48 } 49 Status EnQueue(LinkQueue &Q,QElemType e) 50 { 51 QueuePtr p=(QueuePtr)malloc(sizeof(QNode)); 52 if(!p) 53 exit(OVERFLOW); 54 p->data=e; 55 p->next=NULL; 56 Q.rear->next=p; 57 Q.rear=p; 58 return OK; 59 } 60 Status DeQueue(LinkQueue &Q,QElemType &e) 61 { 62 if(Q.front==Q.rear) 63 return ERROR; 64 QueuePtr p=Q.front->next; 65 e=p->data; 66 Q.front->next=p->next; 67 if(Q.rear==p) 68 Q.rear=Q.front; 69 free(p); 70 return OK; 71 } 72 Status QueueEmpty(LinkQueue Q) 73 { 74 if(Q.front==Q.rear) 75 return TRUE; 76 else 77 return FALSE; 78 } 79 typedef struct 80 { 81 int key; 82 }SLNode; 83 typedef struct 84 { 85 SLNode r[maxn]; 86 int length; 87 }SLList; 88 LinkQueue B[Radix]; 89 int Ord(int k,int j) 90 { 91 for(int i=1;i<j;i++) 92 k/=10; 93 k%=10; 94 return k; 95 } 96 void Print_L(SLList L) 97 { 98 int mrk=0; 99 for(int p=1;p<=L.length;p++) 100 { 101 if(mrk) 102 printf(" "); 103 printf("%d",L.r[p].key); 104 mrk=1; 105 } 106 printf("\n"); 107 } 108 void Distribute(SLList &L,int i) 109 { 110 for(int j=1;j<=L.length;j++) 111 { 112 int k=Ord(L.r[j].key,i); 113 EnQueue(B[k],L.r[j].key); 114 } 115 } 116 void Collect(SLList &L) 117 { 118 int i=1; 119 for(int j=1;j<Radix;j++) 120 { 121 while(!QueueEmpty(B[j])) 122 DeQueue(B[j],L.r[i++].key); 123 } 124 } 125 void RadixSort(SLList &L) 126 { 127 for(int i=0;i<Radix;i++) 128 { 129 InitQueue(B[i]); 130 } 131 for(int i=1;i<=6;i++) //最高位数为6,可根据实际变化 132 { 133 Distribute(L,i); 134 Collect(L); 135 } 136 } 137 int main() 138 { 139 int n; 140 scanf("%d",&n); 141 SLList L; 142 L.length=n; 143 for(int i=1;i<=n;i++) 144 { 145 scanf("%d",&L.r[i].key); 146 } 147 RadixSort(L); 148 Print_L(L); 149 return 0; 150 }
顺序时间复杂度:
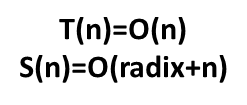
(由于我们所用教材为严蔚敏老师编写的,所以代码风格接近,也易于读懂。
坚持不懈地努力才能成为大神!




