Java数学函数 Math.atan2()详解

前言

今天在刷leetcode题时用到了atan2()函数，确实之前没用过这个函数，只知道Math库里面有反正切函数atan()、反正弦asin()、反余弦acos()，感觉功能挺强大的，趁机也学习一下。

介绍

Java中的Math.atan2(double x, double y)方法功能如下：

将指定的直角坐标(x, y)转换为极坐标(r, θ)，并返回弧度θ。

该方法通过计算 y/x 的反正切值来计算弧度θ，值域为(-π, π]。

具体理解请看下图：

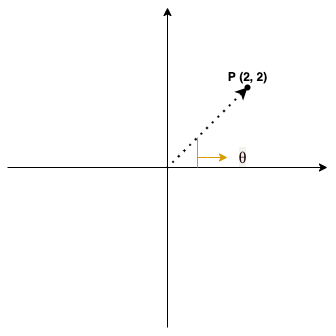
给定一个点P (2, 2)，利用θ=atan2(2, 2)函数求得的θ即为图中所示的角，可以直观看出θ是P与原点O所连直线和x轴的夹角。

如果给定两个点P1，P2，想求出这两点连线与水平线的夹角该如何求呢？实际上很简单，做一下简单的坐标变换即可，如下图所示：

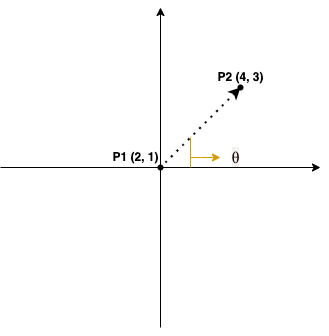
我们将坐标轴进行平移，使P1与原点O重合，那么现在的情况就与上一种情况并无不同了，但是计算θ的方法变为θ=atan2(y2-y1, x2-x1)=atan2(2, 2)。这样便可求出这两点连线与水平线的夹角了。

atan2与atan区别

这两个函数都是反正切函数，究竟有什么不同呢？

1. 参数个数不同：atan(double a)，而atan2(double y, double x)。
2. 参数含义不同：atan中的参数a一般传y/x，也就是斜率，而atan2中的两个参数就是实际中的x坐标和y坐标。
3. 值域不同：atan值域为\([-\frac{\Pi}{2}, \frac{\Pi}{2}]\)，而atan2的值域为\((-\Pi, \Pi]\)。

通过上述不同可以看出atan传递的参数为y/x，这样便会无法分辨在一三象限的x和y绝对值相同的点以及在二四象限的x和y绝对值相同的点。而atan2是可以通过不同的θ区分的。

具体使用

public class MainClass {
    public static void main(String[] args) {
        double x = 2, y = 2;
        System.out.println(Math.atan2(y, x)); // 0.7853981633974483
        System.out.println(Math.atan(y / x)); // 0.7853981633974483
        double x2 = 4, y2 = 3;
        double x1 = 2, y1 = 1;
        System.out.println(Math.atan2(y2 - y1, x2 - x1)); // 0.7853981633974483
        System.out.println(Math.atan((y2 - y1) / (x2 - x1))); // 0.7853981633974483
        // 下面有区别
        System.out.println(Math.atan2(y1 - y2, x1 - x2)); // -2.356194490192345
        System.out.println(Math.atan((y1 - y2) / (x1 - x2))); // 0.7853981633974483
    }
}

总结

针对atan2和atan函数，建议均使用atan2函数。这样无需额外判断便可得到不同象限的角。