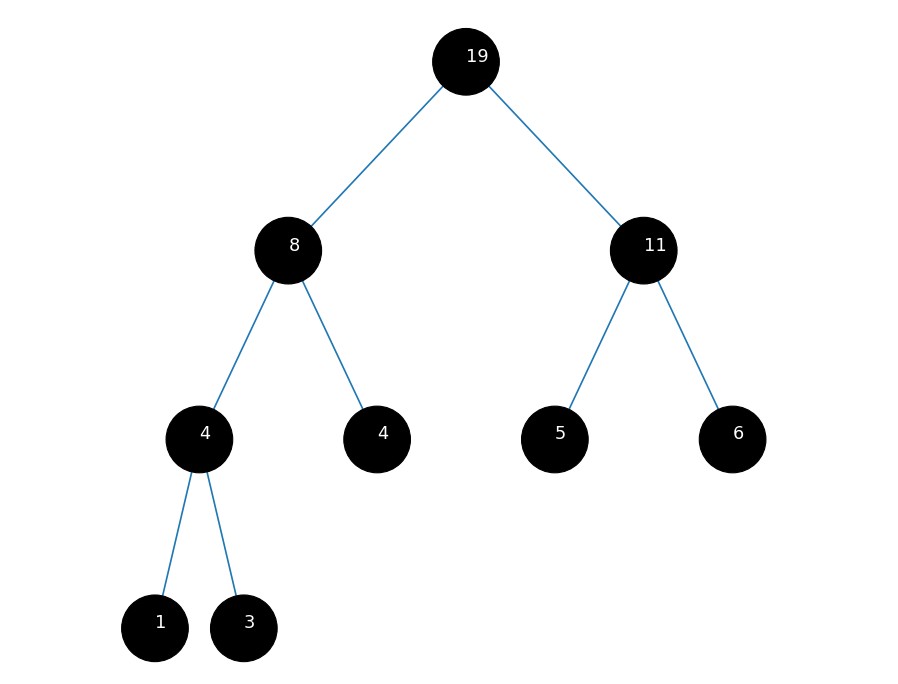
二叉树可视化 - 哈夫曼树
哈夫曼树可视化
import matplotlib.pyplot as plt
class Tree:
def __init__(self, weight=None, left=None, right=None):
self.weight = weight
self.left = left
self.right = right
self.is_red = False
def get_height(self): # 返回树高度,未优化算法应该比较慢
layers = [self]
layer_count = 0
while layers:
layer_count += 1
new_list = []
for node in layers:
if node.left:
new_list.append(node.left)
if node.right:
new_list.append(node.right)
layers = new_list
return layer_count
def visualize(self, axis='off'):
''' 可视化树结构
基本算法: 将树状结构映射到二维矩阵中,
如果节点左右下方有节点则把该节点加入到矩阵中的坐标中,
如节点(x,y)左下方有节点则把节点放入(x+offset,y+1)
offset为x坐标偏移量,
offset = 2**(len(matrix)-y-2)
'''
FONT_SIZE = 16
NODE_SIZE_SCALE = 1.5
figure, axes = plt.subplots(figsize=(8, 6), dpi=80)
height = self.get_height()
width_ = 2 ** (height - 1)
width = 2 * width_ + 1
matrix = [[[] for x in range(width)] for y in range(height)]
matrix[0][width_] = self # put head in the middle position
for y in range(len(matrix)):
for x in range(len(matrix[y])):
node = matrix[y][x]
if node:
x1, y1 = (1 / width) * (x + 0.5), 1 - (1 / height) * y - 0.2
axes.text(x1, y1, str(node.weight), color='white', fontsize=FONT_SIZE)
offset = 2 ** (len(matrix) - y - 2)
if node.left:
matrix[y + 1][x - offset] = node.left
x2, y2 = (1 / width) * (x - offset + 0.5), 1 - (1 / height) * (y + 1) - 0.2
line = mlines.Line2D([x1, x2], [y1, y2], zorder=-1)
axes.add_line(line)
if node.right:
matrix[y + 1][x + offset] = node.right
x2, y2 = (1 / width) * (x + offset + 0.5), 1 - (1 / height) * (y + 1) - 0.2
line = mlines.Line2D([x1, x2], [y1, y2], zorder=-1)
axes.add_line(line)
cc = plt.Circle(((1 / width) * (x + 0.5), 1 - (1 / height) * y - 0.2),
1 / width / 2 * NODE_SIZE_SCALE,
color=('r' if node.is_red else 'black'))
axes.set_aspect(1)
axes.add_artist(cc, )
plt.axis(axis)
plt.show()
class HuffmanTree:
"""哈夫曼树(huffmanTree)
构建方法:
将几点根据权重大小放到最小堆中,先从做小堆中取出两个最小元素,构成一棵树,根节点权重为两子树的和。然后将根节点插入堆中,依次上边操作,
共计操作数据长度-1次,此时堆中只有一个元素,就是哈夫曼树的根节点。WPL等于根节点的权重值。
"""
def __init__(self, element: list):
self._element = element
self._size = len(element) + 1
self._used = 0
self._case = [None for _ in range(self._size)]
def _is_full(self):
return self._used > self._size
def insert(self, root: Tree):
"""往堆中插入元素"""
if self._is_full():
return 'is full'
self._used += 1
add_node = self._used
father = self._used // 2
while father:
if root.weight > self._case[father].weight:
break
self._case[add_node] = self._case[father]
add_node = father
father //= 2
self._case[add_node] = root
def delete(self):
"""从堆中删除元素"""
if self._used == 0:
return 'is empty'
root = 1
res = self._case[root]
# node = self._used
while True:
left_son = root * 2
right_son = left_son + 1
if left_son < self._used and self._case[left_son].weight <= self._case[right_son].weight and self._case[
left_son].weight < \
self._case[self._used].weight:
self._case[root] = self._case[left_son]
root = left_son
elif right_son < self._used and self._case[right_son].weight <= self._case[left_son].weight and self._case[
right_son].weight < \
self._case[self._used].weight:
self._case[root] = self._case[right_son]
root = right_son
else:
break
self._case[root] = self._case[self._used]
self._case[self._used] = None
self._used -= 1
return res
def create(self):
"""构建哈夫曼树"""
for i in self._element:
tree = Tree(i)
self.insert(tree)
for _ in range(self._size - 2):
left = self.delete()
right = self.delete()
tree = Tree(left.weight + right.weight, left, right)
self.insert(tree)
tree = self.delete()
return tree
if __name__ == '__main__':
# heap = Heap()
a = [3, 1, 4, 5, 6]
huff = HuffmanTree(a)
r = huff.create()
# t = Tree()
r.visualize() # 可视化树结构
效果展示