bfs&dfs

如下图

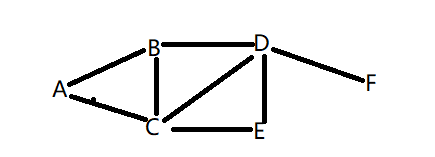
bfs代码

点击查看代码

"""
bfs算法:
    存储：将每个节点的相邻节点用key:value的形式存在字典中
    遍历：从起点开始，先把起点(key)的值(value)取出，然后检查取出的值是否已经被执行过，没有则继续取(key)出其值(value)执行前边的步骤
"""
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'C', 'D'],
    'C': ['A', 'B', 'D', 'E'],
    'D': ['B', 'C', 'E', 'F'],
    'E': ['C', 'D'],
    'F': ['D']

}


def bfs(graph, start):
    queue = [start]  # 待遍历的节点，是一个队列
    check = set(start)  # 已经走过的节点
    result = list()  # 结果
    while len(queue) > 0:
        node = queue.pop(0)  # 出队
        result.append(node)
        for el in graph[node]:
            if el not in check:  # 过滤已经走过的节点
                check.add(el)
                queue.append(el)  # 入队

    return result

dfs代码

dfs是将bfs中待遍历节点的存储结构从队列换成栈

点击查看代码

def dfs(graph, start):
    stack = [start]  # 待遍历的节点，是一个栈
    check = set(start)  # 已经走过的节点
    result = list()  # 结果
    while len(stack) > 0:
        node = stack.pop() # 出栈
        result.append(node)
        for el in graph[node]:
            if el not in check:  # 过滤已经走过的节点
                check.add(el)
                stack.append(el)

    return result

一个博客

https://blog.csdn.net/Huangkaihong/article/details/106131950