Algorithm I assignment Collinear
这本来应该是第三周的作业,但是由于其他作业逼近deadline,暂时推后了一周完成。
这周的assignment大大提高了我对这门课的看法,不得不说,Algorithms这门课的assignment部分设计得很好。为什么好?个人认为有以下几点:
- 程序要求解耦
- 循序渐进,这周的作业不允许使用hashcode()
- 输入变量不允许被程序改变
能做到1、3两点,在工程中也是高质量代码的体现
题目很简单,即给出一个点集,找所有出任意四点或以上共线的线段,将该线段的端点new 一个segment()对象存起来。看起来很简单,实际上到处都是坑TAT
第一部分是用brute force的方法做,由于4个及以上的点才是共线,这里要求中提出为了简化,brute方法不考虑5个及以上的点。所以既是对点集进行4层循环即可,时间复杂度是O(n4)。
但是这里需要注意的是,输入的点集,不能被直接操作,必须被赋值为拷贝才行,否则,外界如果更改了点集中的点,则会影响结果。这一点还说明了,java都是值传递,传进来的是一个数组引用的copy。
另外辩解条件必须要注意,其实挺容易出错的。

1 public class BruteCollinearPoints { 2 // finds all line segments containing 4 points 3 private int N; 4 private ArrayList<LineSegment> segment = new ArrayList<LineSegment>(); 5 6 public BruteCollinearPoints(Point[] points) { 7 if (points == null) 8 throw new java.lang.NullPointerException(); 9 N = 0; 10 Point[] copy = new Point[points.length]; 11 for (int i = 0; i < points.length; i++) { 12 copy[i] = points[i]; 13 } 14 Arrays.sort(copy); 15 for (int i = 0; i < copy.length - 1; i++) { 16 if (copy[i].compareTo(copy[i + 1]) == 0) { 17 throw new java.lang.IllegalArgumentException(); 18 } 19 } 20 for (int i = 0; i < copy.length - 3; i++) { 21 for (int j = i + 1; j < copy.length - 2; j++) { 22 double slope1 = copy[i].slopeTo(copy[j]); 23 for (int k = j + 1; k < copy.length - 1; k++) { 24 double slope2 = copy[i].slopeTo(copy[k]); 25 if (slope1 != slope2) 26 continue; 27 int temp = 0; 28 for (int l = k + 1; l < copy.length; l++) { 29 double slope3 = copy[i].slopeTo(copy[l]); 30 if (slope1 == slope3) 31 temp = l; 32 if ((l == copy.length - 1) && (temp != 0)) { 33 N++; 34 segment.add(new LineSegment(copy[i], copy[temp])); 35 } 36 } 37 } 38 } 39 } 40 } 41 42 // the number of line segments 43 public int numberOfSegments() { 44 return N; 45 } 46 47 // the line segments 48 public LineSegment[] segments() { 49 LineSegment[] results = new LineSegment[N]; 50 for (int i = 0; i < N; i++) { 51 results[i] = segment.get(i); 52 } 53 return results; 54 } 55 56 public static void main(String[] args) { 57 58 // read the N points from a file 59 // In in = new In(args[0]); 60 In in = new In("./collinear/rs1423.txt"); 61 int N = in.readInt(); 62 System.out.println(N); 63 Point[] points = new Point[N]; 64 for (int i = 0; i < N; i++) { 65 int x = in.readInt(); 66 int y = in.readInt(); 67 System.out.println("x:" + x + " y:" + y); 68 points[i] = new Point(x, y); 69 } 70 71 // draw the points 72 StdDraw.show(0); 73 StdDraw.setXscale(0, 32768); 74 StdDraw.setYscale(0, 32768); 75 for (Point p : points) { 76 p.draw(); 77 } 78 StdDraw.show(); 79 80 // print and draw the line segments 81 BruteCollinearPoints collinear = new BruteCollinearPoints(points); 82 for (LineSegment segment : collinear.segments()) { 83 StdOut.println(segment); 84 segment.draw(); 85 } 86 } 87 }
由于这个方法时间复杂度太高,于是提出一种N2 log N 的方法,核心思路就是,通过实现一个排序方法,使点始终保持有序性来提高效率。看到N*NlogN,就想到了遍历点后排序,orz。下面是官方给出的算法描述:
- Think of p as the origin.
- For each other point q, determine the slope it makes with p.
- Sort the points according to the slopes they makes with p.
- Check if any 3 (or more) adjacent points in the sorted order have equal slopes with respect to p. If so, these points, together with p, are collinear.

实现的思路就是:
- 对所有点排序,越靠近左下角的点越小
- 遍历每一个点,遍历点P过程中,先将其他点根据与P的斜率进行排序
- 对排序后的其他点进行遍历,若有斜率相同超过4个以上的点,即是要找的线段
按照这个思路,很快就实现除了代码,需要注意的除了边界等细节问题,再有就是,如何避免子线段和重复线段。这两个问题把我卡住很久。
先说如何解决子线,所谓子线段就是原本线段:a->b->c->d->e是符合条件的,我将其取出,但是我又把b->c->d->e也当作新的线段取出来了。一开始的思路是,每次遍历一个点,都将其所有在一条线段上的点找出来,然后将这些点集sort一下,取最大最小。即在搜寻b的时候,将a,c,d,e和其本身b进行排序,取最小a和最大e。这样问题就解决了,但是同样还有一个问题是,由于每个点都进行了这样的操作,会导致有很多重复的线段。通过a得到线段(a,e),通过b又得到一边(a,e),所以结果是需要去重的。非常自然的想到了hashset,保证了时间复杂度不高。
然而使用hashcode的思路都无法实现...原因是poin和segment两个class都继承了Object的hashcode()方法,但是仅仅是在调用时抛出异常...至于为何会这样,原因是第三周还没有讲到hashtable这个数据结构orz
这条路不行,退一步,用toString()方法,将其toString后,存入hashset,来检查是否有重复的线段。我太机智了。不过这样依然是不是100%的通过,看了下testcase,竟然有一条fail是说我不应该依赖于toString()方法...
为什么不让?我陷入了沉思,comment中提到,这个方法仅供debug用,不要用于实现算法...不过细想其实是非常有道理的。我的算法本身实际上是依赖于comparable接口以及camparator的实现。而不是依赖于point和segment这两个具体的类。所以本身我就不应该去依赖于这两个类其他的方法,用了toString()只能说是非常tricky的方法。这样的做法,做到了解耦。看到这个testcase,感觉自己和名校的学生差距就是在这些细节上拉开的。不做这样的题,意识不到interface到底有啥用,不就是定义了几个未实现的方法吗?可是正是通过约定好的接口,做到了解耦。以后如果有人要修改point toString(),依然不会影响到我的程序的正确性。这就无形中提高了效率。
好了,回来说说我是怎么解决这个问题的。注意到,我在遍历之前,就先sort了点,这个sort有啥用呢?这个sort意味着,等会对于每个点找共线线段时,是按照从左下往右上的顺序来的,看图说话:
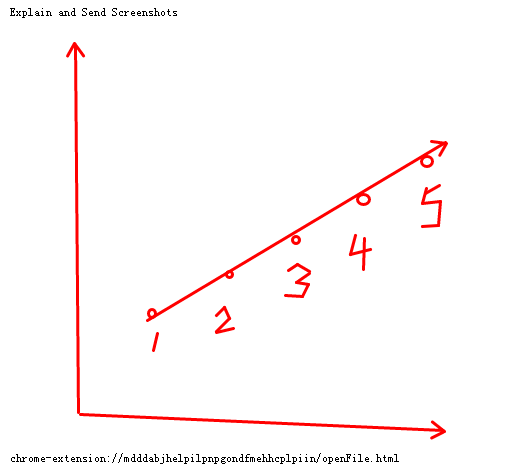
排过序的点是按照1,2,3,4,5的顺序来遍历的。当选取点1时,找到共线的5个点{1,2,3,4,5},因此我们选择最大最小作为线段(1,5)。
当选取点2时,找到了共线的5个点{1,2,3,4,5},这里也这里发现2<1,由于有序性,我们可以确认在此之前就有(1,5)被选取过了,所以这次的选择可以直接跳过。
这意味着,只要是当前遍历的点P不是共线点集中最小的点,我们都可以直接抛弃。这样就完美避免了重复的线段。
至此,根据这个方案,这个assignment圆满解决了。
一下是fast方法的实现,其他的代码就不贴了。

package collinear; import java.util.ArrayList; import java.util.Arrays; import java.util.Collections; import java.util.HashMap; import java.util.HashSet; import edu.princeton.cs.algs4.In; import edu.princeton.cs.algs4.StdDraw; import edu.princeton.cs.algs4.StdOut; public class FastCollinearPoints { private int N; private ArrayList<LineSegment> segment = new ArrayList<LineSegment>(); private Point[] points; public FastCollinearPoints(Point[] points) { if (points == null) throw new java.lang.NullPointerException(); this.points = new Point[points.length]; for (int i = 0; i < points.length; i++) { this.points[i] = points[i]; } N = 0; Arrays.sort(this.points); // remove repeat points for (int i = 0; i < this.points.length - 1; i++) { if (this.points[i].compareTo(this.points[i + 1]) == 0) { throw new java.lang.IllegalArgumentException(); } } Point[] temp = new Point[this.points.length]; Point[] copy = new Point[this.points.length]; ArrayList<ArrayList<Point>> end_sets = new ArrayList<>(); // use a copy to sort for (int i = 0; i < this.points.length; i++) { temp[i] = copy[i] = this.points[i]; end_sets.add(new ArrayList<Point>()); } Arrays.sort(copy); // to sort by slope for (int i = 0; i < copy.length - 1; i++) { Arrays.sort(temp, copy[i].slopeOrder()); // find same slope copy then save them as segment in segment // ArrayList int count = 1; double slope0 = copy[i].slopeTo(temp[0]); ArrayList<Point> set = new ArrayList<>(); for (int j = 0; j < temp.length; j++) { // record max point double slope1 = copy[i].slopeTo(temp[j]); if (slope1 == slope0) { set.add(temp[j]); count++; if (count > 2 && j == temp.length - 1) { set.add(copy[i]); Collections.sort(set); // System.out.println(set); if (set.get(0).compareTo(copy[i]) < 0) { } else { // no key, no set segment.add(new LineSegment(set.get(0), set.get(set.size() - 1))); N++; } count = 1; } } else { if (count > 2) { set.add(copy[i]); Collections.sort(set); // System.out.println(set); if (set.get(0).compareTo(copy[i]) < 0) { } else { // no key, no set segment.add(new LineSegment(set.get(0), set.get(set.size() - 1))); N++; } } set = new ArrayList<>(); set.add(temp[j]); count = 1; } slope0 = slope1; } } } // the number of line segments public int numberOfSegments() { return N; } // the line segments public LineSegment[] segments() { LineSegment[] results = new LineSegment[N]; for (int i = 0; i < N; i++) { results[i] = segment.get(i); } return results; } public static void main(String[] args) { // read the N points from a file // In in = new In(args[0]); In in = new In("./collinear/rs1423.txt"); int N = in.readInt(); // System.out.println(N); Point[] points = new Point[N]; for (int i = 0; i < N; i++) { int x = in.readInt(); int y = in.readInt(); // System.out.println("x:" + x + " y:" + y); points[i] = new Point(x, y); } // draw the points StdDraw.show(0); StdDraw.setXscale(0, 32768); StdDraw.setYscale(0, 32768); for (Point p : points) { p.draw(); } StdDraw.show(); // // print and draw the line segments FastCollinearPoints collinear = new FastCollinearPoints(points); for (LineSegment segment : collinear.segments()) { StdOut.println(segment); segment.draw(); } } }
老规矩,亮下分数:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号