模和同余定理
一、什么是余数
在整数的除法中,只有能整除与不能整除两种情况。当不能整除时,就产生余数。我们在读小学二年级时,已经学了带余数的出发了,我们来温习一下。
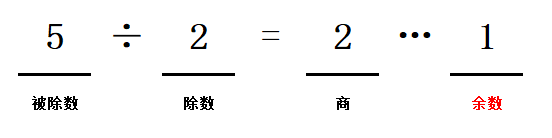
通过做了这么多年除法,我们可以理解到,余数是指整数除法中被除数未被除尽部分,且余数的取值范围为0到除数之间(不包括除数)的整数,也就是说余数一定比除数小。一个数除以另一个数,要是比另一个数小的话,商为0,余数就是它自己。
二、余数的性质
- 余数和除数的差的绝对值要小于除数的绝对值(适用于实数域
被除数=除数×商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数;余数=被除数-除数×商。
- 如果a,b除以c的余数相同,那么a与b的差能被c整除。例如,17与11除以3的余数都是2,所以17-11能被3整除。
- a与b的和除以c的余数(a、b两数除以c在没有余数的情况下除外),等于a,b分别除以c的余数之和(或这个和除以c的余数)。例如,23,16除以5的余数分别是3和1,所以(23+16)除以5的余数等于3+1=4。注意:当余数之和大于除数时,所求余数等于余数之和再除以c的余数。例如,23,19除以5的余数分别是3和4,所以(23+19)除以5的余数等于(3+4)除以5的余数。
- a与b的乘积除以c的余数,等于a,b分别除以c的余数之积(或这个积除以c的余数)。例如,23,16除以5的余数分别是3和1,所以(23×16)除以5的余数等于3×1=3。注意:当余数之积大于除数时,所求余数等于余数之积再除以c的余数。例如,23,19除以5的余数分别是3和4,所以(23×19)除以5的余数等于(3×4)除以5的余数。
三、三大余数定理
- 加法定理
a与b的和除以c的余数,等于a、b分别除以c的余数之和,或这个和除以c的余数。
比如:
23÷5=4.....3
16÷5=3.....1
(23+16)÷5=7.....(4=3+1) - 乘法定理
a与b的积除以c的余数,等于a、b分别除以c的余数之积,或这个积除以c的余数。
比如:
23÷5=4.....3
16÷5=3.....1
(23X16)÷5=73.....(3=3X1) - 同余定理
若两个整数a、b被自然数m除有相同的余数,那么称a、b对应模m同余,记为同余式a≡b (mod m)。由同余的性质,我们可以得到一个推论:若a、b同余,则a、b的差一定能被m整除,记为如果a≡b (mod m),那么一定有a-b=mk,k为整数。
四、模的理解
结合余数的定义、性质和同余定理,我们可以这样去理解:模就像是一个计量系统的计数范围,实质上是计量系统产生“溢出”的量,它的值在计量器上表示不出来,计量器上只能表示出模的余数。如时钟只能表示0~11点的数值,12则是该时钟的模,当值大于等于12时,则需要对时钟的模(12)进行取余运算,得到该计量系统的值。
还是以时钟计量系统位例,假设当前时针指向11点,而准确时间是8点,调整时间可有以下两种拨法:
- 一种是倒拨3小时,即:
11-3=8 - 另一种是顺拨9小时:
11+9=12+8=8
在以模为12的系统中,加9和减3效果是一样的,因此凡是减3运算,都可以用加9来代替。对“模”12而言,9和3互为补数(二者相加等于模)。
所以我们可以得出一个结论,即在有模的计量系统中,当某个值A, 需要做一个减法运算(A - B = X),得到某个想要的结果X时。我们可以化减为加,使得A + C也能得到想要的结果X。那么B和C就是互为补数,他们相加得到的值就是该计量系统的模,减B和加C的行为是同余的,既(A - B) mod 模 = X ,(A + C) mod 模 = X。根据这个结论,我们就不难理解计算机系统采用补码来表示数值了。首先计算机存储有位数限制,比如8位、16位、32位等,那么不同位数的二进制的模等于2n,比如有符号位的8位整数,模为28=256,我们来求一下(-13)10的二进制补码,首先求补数 256-13=243,转为二进制1111 0011,即为(-13)10的补码。




