二进制、八进制、十进制、十六进制的互相转换
在编程工作种，我们时常需要对不同的进制的数进行转换，以方便我们的工作、阅读和理解。在计算机领域，主要设计二进制、八进制、十进制和十六进制，下面我们就来讲讲这四种机制的整数相互转换方法。
一、查表法
就是我们制作一张包含各种进制的值一 一对应数值表，需要时查表就得，但是，我们知道，这不太现实，因为数是无穷的，我们不可能做一张无穷的表。在次但是，这也不是说查表法就不用了，其实我们一直在使用，你可能会说，没有，没见过，不对，有的，就在你的脑海里，我相信绝大部分程序员都有，比如，问你，(15)10对应的十六进制是多少，你肯定张口就答(F)16，为什么你能很快答出，是因为我们在日常工作和学习中，无形在脑海里建立了这张表。只是这张表很有限，更大的数你就不能一口答了，所以需要其他的转换方法，但是其他方法会用到查表法。
我们至少要建立起如下的一张表
二、短除法
短除法运算方法是先用一个除数除以能被它除尽的一个质数，以此类推，除到商是质数为止。具体在我们的进制换算里，当一个M进制数转N进制数时，就是用这个数除N取余，逆序排列。具体做法是：将N作为除数，用M进制整数除以N，可以得到一个商和余数；保留余数，用商继续除以N，又得到一个新的商和余数；仍然保留余数，用商继续除以N，还会得到一个新的商和余数；如此反复进行，每次都保留余数，用商接着除以N，直到商为0时为止
下面举例：
- 十进制转二进制、八进制、十六进制
(10)10--->(x)2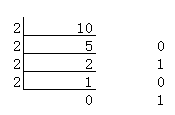
结果为(10)10--->(1010)2
(100)10--->(x)8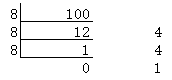
结果为(100)10--->(144)8 。
(100)10--->(x)16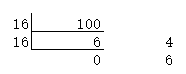
结果为(100)10--->(64)16 - 八进制转二进制、十进制、十六进制
(27)8--->(x)2
结果为(27)8--->(10111)2
(27)8--->(x)10
首先查表得 (10)10<===>(12)8
有如下算式
结果为(27)8--->(23)10
(756)8--->(x)16
首先查表得 (16)10<===>(20)8
(E)16<===>(16)8
有如下算式
结果，(756)8--->(1EE)16
二进制转其他进制和十六进制转其他进制我就不一一举例了，通过上面的例子，我们可以看到用短除法我们是可以进行任意进制的相互转换的，同时我们也可以发现，将高进制向低进制（只限于这几种进制，我们姑且认为高低顺序为：二进制<八进制<十进制<十六进制）转换时，要先有一步进制基数的查表换算过程，在加上我们人对二、八、十六进制的四则运算不熟悉，所以这三种进制进行短除法换算比较困难。由于十进制的基数本身就是十六进制的数码，同时代表的量意义也一样，所以总的来说，短除法特别适合十进制向二、八、十六进制的转换。
三、位权相加法
我们知道，任何进制的数都是由：位、数码、位权等要素构成，这也为我们进制间的转换提供了一种方法：位权相加法。假设当前数字是N进制，那么：对于整数，从右往左看，第i位的位权等于Ni-1。更加通俗的理解是，假设一个多位数（由多个数字组成的数）某位上的数字是1，那么它所表示的数值大小就是该位的位权。当我们由M进制转为N进制时要进行这样的运算：a*Ni-1+aNi-2+...+a*N1+a*N0。
下面举例：
- 二进制转十进制
转换公式：a*2i-1+a*2i-2+...+a*21+a*20
(11001)2=1*24+1*23+0*22+0*21+1*20=(16+8+0+0+1)10=(25)10 - 八进制转十进制
转换公式：a*8i-1+a*8i-2+...+a*81+a*80
(145)8=1*82+4*81+5*80=(64+32+5)10=(101)10 - 十六进制转十进制
转换公式：a*16i-1+a*16i-2+...+a*161+a*160
(145)16=1*162+4*161+5*160=(256+64+5)10=(325)10 - 二进制转八进制
由于两个进制的基数存在着这样的关系 8=23，也就是说3为二进制数正好是一位八进制数。所以只能是从低到高，按3位一组编组，高位不够3位补0，在编组内用二进制转十进制的公式
(11001)2=(011)2( 001)2=(0*22+1*21+1*20)(0*22+0*21+1*20)=(31)8 - 二进制转十六进制
由于两个进制的基数存在着这样的关系 8=24，也就是说4为二进制数正好是一位十六进制数。所以只能是从低到高，按4位一组编组，高位不够4位补0，在编组内用二进制转十进制的公式
(11001)2=(0001)16( 1001)16=(0*23+0*22++0*21+1*20)(1*23+0*22++0*21+1*20)=(19)16
我们可以看到，位权相加法特别适合二、八、十六进制转十进制，对其它情况则很困难，比如二进制转八、十六进制时先用了合位法，特别是高进制转低进制更是困难。
四、拆位拼接法
由于二进制、八进制和十六进制的基数有着这样的关系：8=23，16=24，也就十说一位八进制数等于3位二进制数，一位十六进制数等于4位二进制数，所以有如下转换方法。
- 八进制转二进制
一位八进制数通过查表拆成三位二进制，然后按八进制数的高低位组合起来即可。如：
( 2743)8---->(x)2
先拆成：2 7 4 3，然后分别查表对应的二进制 010 111 100 011
然后拼接，结果为( 2743)8---->(010111100011)2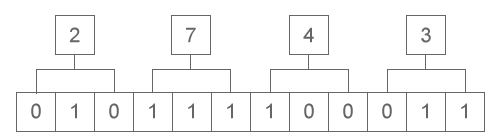
- 十六进制转二进制
一位十六进制数通过查表拆成四位二进制，然后按十六进制数的高低位组合起来即可。如：
( A5D6)16---->(x)2
先拆成：A 5 D 6，然后分别查表对应的二进制 1010 0101 1101 0110
然后拼接，结果为( A5D6)16---->(1010010111010110)2
五、借桥法
对某些困难的情况，我们可以先转位十进制或二进制，然后在转为对应的进制，我成为借桥法，中间的进制就是桥。比如十六进制转八进制，我们可以先用位权相加法转为十进制，在用短除法转为八进制。这就不举例了。
六、总结
- 短除法和位权相加法都能进行这四种进制的相互转换，只是在某些情况下较困难
- 十进制转二、八、十六进制时最好用短除法
- 二、八、十六进制转十进制时最好用位权相加法
- 二进制转八、十六进制最好用合位法和位权相加法
- 八、十六进制二转进制最好用拆位拼接法
- 八进制和十六进制的互相转换最好用用借桥法
