十进制和二进制的运算---我所理解到的人类的运算的本质

数，存在于宇宙的各个角落，不管有没有人类的存在，它都存在。只是在于有没有被我们发现。还好，人类发展至今，发现了各种数：自然数、分数、实数、虚数等。我们今天来说下自然数里的基本运算，也就是我们小学一二年级里学的四则运算：加减乘除。想想我们的学习过程：首先掰手指数数、识数、数的组合和拆分、10以内的加减法、100以内的加减发、乘法和除法。老师不断的讲解，我们不断的练习、考试、口算、背乘法表等，这一切为了什么。为的是给我们今后的学习打下基础。这个基础就是10进制数的数列表、加法表、乘法表，让这些表深深的存储在我们的脑海里。善于学习的人，他们还存储了减法表和除法表。所以当我们人类进行四则运算时，我们大脑其实是在不停的查表，在这五张表里交叉查询，灵活运用，完成运算得出结果。

一、十进制的运算

我以我们最熟悉的十进制数来举例，首先我们建立20以内的一个自然数列：

0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19

在数列里完成加法：4+7，以4为起点，从0开始计数查表，往右走7步是11，所以我们得出4+7=11；

在数列里完成减法：18-6，以18为起点，从0开始计数查表，往左走6步是12，所以我们得出18-6=12；

在数列里完成乘法：2X7,由于0乘任何数都等于0，所以我们从1开始，2个数一步进往右查7次是14，所以我们得出2*7=14；

在数列里完成除法：在单纯的自然数列里，我没右找到除法怎么查表，应该是无法完成，聪明的你想到了告诉我。

 

如上，只是在单纯的自然数列里，做四则运算有如下缺点：

• 当数过大时，太麻烦，效率不高
• 无法完成除法

我们聪明的大脑在我们认真的学些的过程中，建立了两个表：加发表和乘法表

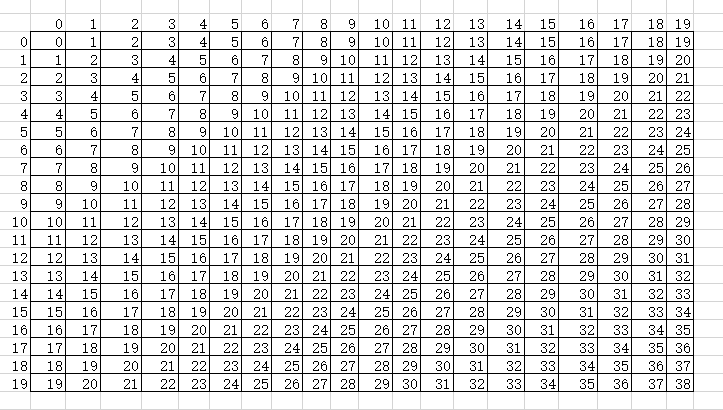
• 加法表
  

  用加法表做加法：4+7，直接在上表，横向找到4，纵向找到7，查表得11，所以4+7=11

  用加法表做减法：18-6，横向找到6，在这一列，纵向找到18，在往左找到18对应的开始一列的单元格的值是12，所以18-6=12
  
  
• 乘法表
  
  
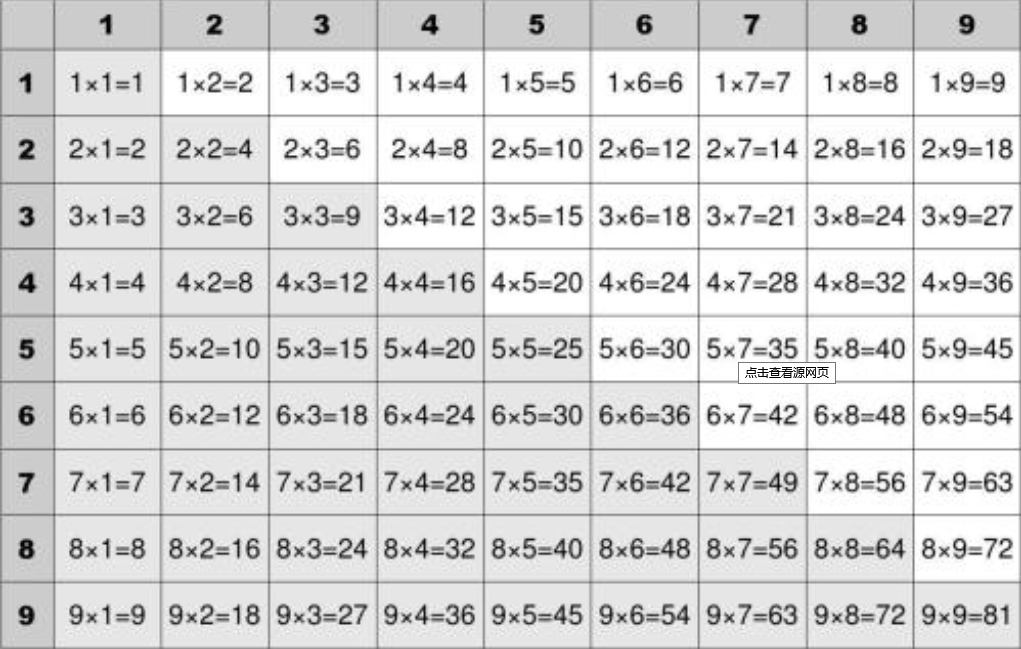
  用乘法表来做乘法：2X7，直接在上表，横向找到2，纵向找到7，查表得14，所以2X7=14。
  用乘法表来做除法：24/6,横向找到6，在这一列，纵向找到24，在往左找到24对应的开始一列的单元格的值是4，所以24/6=4。

可以看到，我们只用加法表和乘法表就能完成四则运算，也效率较高，特别是数值较大时比第一种优势较大。谁打脑海里的表大，内容丰富，谁就会计算得快。但这种方式也是有缺陷的，那就是数是无穷的，也就是这表是无穷大，谁也不可能存储完整的表，因为这本身就是不可能完成的任务，聪明的人类其实是这样做的：由于人类记忆有限，而数是无穷的，对普通人，我们采取的是按位分步计算，这样一来，我们只需存储10以内的表了，然后记住进位/借位规则就能快速正确的计算。如下图：

 

二、二进制运算

上面讲了，我们最熟悉的十进制四则运算，现在奖下我们程序员最熟悉的二进制数，他们是怎么运算的呢。其实是跟十进制一模一样的，都是查表，只是我们绝大多数人对它不熟悉，或者没用过，不了解，但我们程序员是一定要建立起对应的加发表和乘法表，方便我们处理工作种的问题。我们以加发表举例。

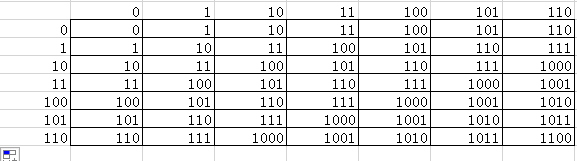
• 加法表
  

  
  做加法：10+11，横向找到10，纵向找到11，查表得101，所以10+11=101。
  做减法：1011-101，横向找到101，在这一列，纵向找到1011，在往左找到1011对应的开始一列的单元格的值是110，所以1011-101=110

乘法除法我就不举例，大家可以看到二进制跟十进制算法一模一样，只是我们别的进制的不熟悉而已。

三、总结

• 运算快的人，其实就是建立的表多、表大、内容丰富
• 查表是我们人类与生俱来的本能
• 不同进制的四则运算其实就是查表，也证明了不同进制是各自成体系，且具备系统完备性
• 在我们计算机编程里，查表是最基础的算法，它的特性就是以存储空间换时间