1. 马尔科夫决策过程
马尔科夫特性:
下一时刻的状态只与现在的时刻的状态相关,与之前的时刻无关,即状态信息包含了历史的所有相关信息。
马尔科夫奖励过程,$<S, P, R, \gamma>$:
$S$是有限状态集
$P$是状态转移概率矩阵,${p_{ss'}} = {\rm P}[{S_{t + 1}} = s'|{S_t} = s]$
$R$是奖励函数,${R_s} = {\rm E}[{R_{t + 1}}|{S_t} = s]$
$\gamma$是折扣因子
为什么要折扣因子呢
1. 数学上方便定义描述
2. 避免了马尔科夫过程的无限循环
3. 折扣可以表示对未来的不确定性
4. 如果奖励是经济的,即时奖励会比延后奖励带来更多的利润
5. 人/动物 确实会更倾向于即时奖励
6. 也存在无折扣的马尔科夫奖励过程
定义回报$G$是从$t$时刻开始的折扣奖励的总和
${G_t} = {R_{t + 1}} + \gamma {R_{t + 2}} + ... = \sum\limits_{k = 0}^\infty {{\gamma ^k}{R_{t + k + 1}}} $
定义马尔科夫奖励过程的价值函数$v(s)$是状态$s$下的长期价值,即状态$s$下,的期望回报
$v(s) = {\rm E}[{G_t}|{S_t} = s]$
对于马尔科夫奖励过程,为了体现其动态特性,利用贝尔曼方程递推得到:
$v(s) = {\rm E}[{G_t}|{S_t} = s]\\
= {\rm E}[{R_{t + 1}} + \gamma {R_{t + 2}} + {\gamma ^2}{R_{t + 3}} + ...|{S_t} = s]\\
= {\rm E}[{R_{t + 1}} + \gamma ({R_{t + 2}} + \gamma {R_{t + 3}} + ...)|{S_t} = s]\\
= {\rm E}[{R_{t + 1}} + \gamma {G_{t + 1}}|{S_t} = s]\\
= {\rm E}[{R_{t + 1}} + \gamma v({S_{t + 1}})|{S_t} = s]$
$v(s) = {\rm E}[{R_{t + 1}} + \gamma v({S_{t + 1}})|{S_t} = s]$
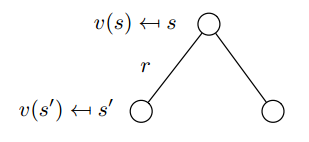
由上图可知,当前状态$s$的价值函数$v(s)$等于
当前状态到下一状态得到的即时奖励$R_s$,加上折扣后的下一状态的价值函数期望值$\gamma \sum\limits_{s' \in S} {{{\rm P}_{ss'}}} v(s')$
$v(s) = {R_s} + \gamma \sum\limits_{s' \in S} {{{\rm P}_{ss'}}} v(s')$
马尔科夫决策过程,$<S, A, P, R, \gamma>$:
引入有限动作空间$A$,将马尔科夫奖励过程转化为马尔科夫决策过程。
$S$是有限状态集
$A$是有限动作集
$P$是状态转移概率矩阵,${p_{ss'}^a} = {\rm P}[{S_{t + 1}} = s'|{S_t} = s, A_t = a]$
$R$是奖励函数,${R_s^a} = {\rm E}[{R_{t + 1}}|{S_t} = s, A_t = a]$
$\gamma$是折扣因子
定义策略$\pi$是在给定状态下的动作分布,$\pi (a|s) = {\rm P}[{A_t} = a|{S_t} = s]$
1. 策略完全定义了智能体的行为
2. 马尔科夫决策过程,决策即动作的选择,依赖于当前状态,与历史状态无关
3. 策略$\pi$是给定状态下的所有动作的概率分布,所以可以求状态转移概率${{\rm P}_{ss'}}$和状态的期望即时奖励$R_s$
${{\rm P}_{ss'}} = \sum\limits_{a \in A} {\pi (a|s){\rm P}_{ss'}^a}$
${R_s} = \sum\limits_{a \in A} {\pi (a|s)R_s^a} $
定义马尔科夫决策过程的价值函数$v_\pi(s)$,在状态$s$下, 服从策略$\pi$,即按照策略$\pi$来选择动作,的期望回报
$v_\pi(s) = {\rm E}[{G_t}|{S_t} = s]$
定义马尔科夫决策过程的动作-值函数$q_\pi(s)$,在状态$s$下,选择动作$a$后, 服从策略$\pi$的期望回报
$q_\pi(s) = {\rm E}[{G_t}|{S_t} = s, A_t = a]$
对于马尔科夫决策过程,为了体现其动态特性,利用贝尔曼方程递推得到:
${v_\pi }(s) = {{\rm{E}}_\pi }[{R_{t + 1}} + \gamma {v_\pi }({S_{t + 1}})|{S_t} = s]$
${q_\pi }(s,a) = {{\rm{E}}_\pi }[{R_{t + 1}} + \gamma {q_\pi }({S_{t + 1}},{A_{t + 1}})|{S_t} = s,{A_t} = a]$

${v_\pi }(s) = \pi (a|s)\sum\limits_{a \in A} {{q_\pi }(s,a)}$ (1)
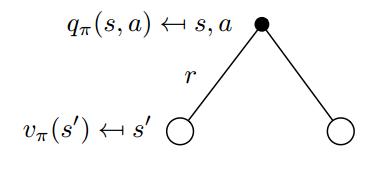
${q_\pi }(s,a) = R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{v_\pi }(s')} $ (2)
把公式(2)带入公式(1),得到${v_\pi }(s)$的贝尔曼递推方程,

${v_\pi }(s) = \sum\limits_{a \in A} {\pi (a|s)\left( {R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{v_\pi }(s')} } \right)} $
把公式(1)带入公式(2),得到${q_\pi }(s,a)$的贝尔曼递推方程,

${q_\pi }(s,a) = R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a\pi (a'|s')\sum\limits_{a' \in A} {{q_\pi }(s',a')} } $
定理:
对于任一马尔科夫决策过程,
1. 一定存在一个最优策略$\pi_*$比其他的所有的策略都好或者相等,$\pi_* \ge \pi, \forall \pi$
2. ${v_{{\pi _*}}(s)} = {v_*}(s)$ ${q_{{\pi _*}}(s, a)} = {q_*}(s, a)$
如果我们知道$q_{{\pi _*}}(s, a)$,就可以每次根据q值,选最大值对应的动作a,从而得到最优策略$\pi$
由于q值是包含了所有未来可能的状态的,所以可以每步贪心就可以了。
贝尔曼最优方程如下:
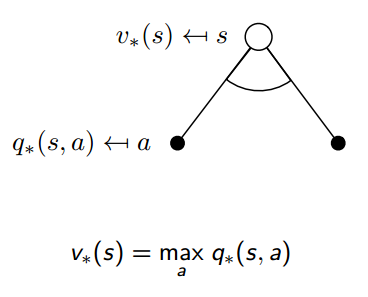
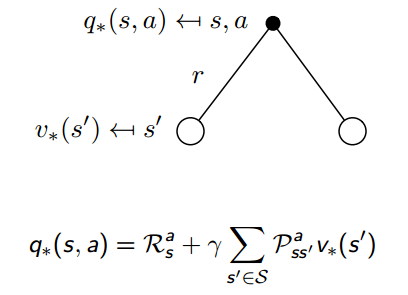
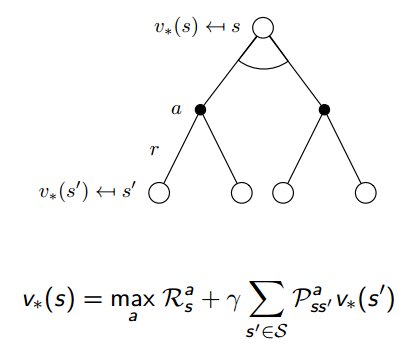

接下来就讲怎么迭代得到最优策略。
参考:
1. David Silver 课程
2. Reinforcement learning: An Introduction. Richard S. Sutton


