paper | Non-Local ConvLSTM for Video Compression Artifact Reduction

摘要

现有的方法使用单个相邻帧或一对相邻帧(在目标帧之前和/或之后)来完成帧质量增强。此外，由于高质量的整体帧可能包含低质量的patch，而高质量的patch可能存在于低质量的整体帧中，因此，目前关注于附近的峰值质量帧(PQFs)的方法可能会忽略低质量帧中的高质量细节。为了弥补这些不足，本文提出了一种利用多个连续帧的新型端到端深度神经网络——非局部卷积神经网络(NL-ConvLSTM)。在NL-ConvLSTM中引入了一种近似的非局部策略来捕获全局运动模式并跟踪视频序列中的时空相关性。该方法利用目标帧的前帧和后帧生成残差，重构出高质量的帧。在两个数据集上的实验表明，NL-ConvLSTM的性能优于现有的方法。

1.介绍

2.相关工作

（这篇文章，涉及到convLSTM和non-local两篇论文，我对convLSTM进行了实现，师兄讲过non-local，有时间再总结它们。）
我们使用NL-ConvLSTM机制来利用多个帧，在不需要显式运动估计和补偿（MFQE需要）的情况下捕获帧序列中的时空变化，采用近似策略进行非局部相似度计算，可以有效地减少伪影，并获得最优的性能。

3.方法

减少视频压缩伪影的目标是从一个压缩过的帧\(X_{t}\)推断出高质量的帧\(\hat{Y}_{t}\).\(X_{t} \in \mathbb{R}^{C \times N}\)是时刻t时的压缩帧。\(C\)是单张帧的channel数，\(N=HW\)，\(N\)是一维的，长度为\(H*W\)，\(H\)是帧的高，\(W\)是帧的宽。\(X_{t} \in \mathbb{R}^{C \times N}\)表示一个(2T+1)连续压缩帧序列，以\(X_{t}\)为输入，\(\hat{Y}_{t}\)为输出。

3.1 框架

我们的方法是一个端到端的可训练框架，由编码器、NL-ConvLSTM模块和解码器三个模块组成，如图2所示。它们分别负责从单独的帧中提取特征，学习帧间的时空相关性，将高层特征解码为残差，最终重构出高质量的帧。

编码器。它采用了几个二维卷积层来提取\(X_{t}\)的特征\(X_{t}\)作为输入，输出为\(\mathcal{F}_{t}=\left\{F_{t-T}, \ldots, F_{t+T}\right\}\)，\(F_{t} \in \mathbb{R}^{C_{f} \times N}\)是从相应的\(X_{t}\)中提取到的特征，\(C_{f}\)是输出特征的channel数。它单独处理每一帧。

NL-ConvLSTM。为了跟踪帧序列中的时空相关性，我们在编码器和解码器之间放置了一个ConvLSTM[41]模块。ConvLSTM能够从任意长度的帧序列中捕获时空信息，但不擅长处理大的运动和模糊运动。为了解决这一问题，我们将non-local[3]机制嵌入到ConvLSTM中，并开发了NL-ConvLSTM模块。这里，非局部相似性用于不同帧的像素，而不是用于帧[3]内的像素。NL-ConvLSTM模块N可以描述为

\[\left[\mathcal{H}_{t}, \mathcal{C}_{t}\right]=\mathcal{N}\left(F_{t-1}, F_{t},\left[\mathcal{H}_{t-1}, \mathcal{C}_{t-1}\right]\right) \]

不同于[37,41]中在t时刻只使用特征\(F_{t}\)送入的ConvLSTM， NL-ConvLSTM 把\(F_{t-1}\)也作为输入。输出相应的hidden state 和 cell state \(\mathcal{H}_{t}, \mathcal{C}_{t} \in \mathbb{R}^{C_{h} \times N}\)。这里，\(C_{h}\)是hidden state和cell state的channel数。此外，\(\mathcal{H}_{t-1}\)和\(\mathcal{C}_{t-1}\)在NL-ConvLSTM中没有直接输入到门操作中.反，我们计算\(F_{t−1}\)和\(F_{t}\)之间的帧间像素相似度\(S_{t}\)，然后对\(H_{t−1}\)和\(C_{t−1}\)以\(S_{t}\)为权重进行加权求和。本文还使用了双向ConvLSTM来学习前后帧的时空依赖性。在接下来的部分中，我们只提到了前向NL-ConvLSTM的操作.关于NL-ConvLSTM模块的详细内容可以参考图2(右)、图3、3.2和3.3部分。

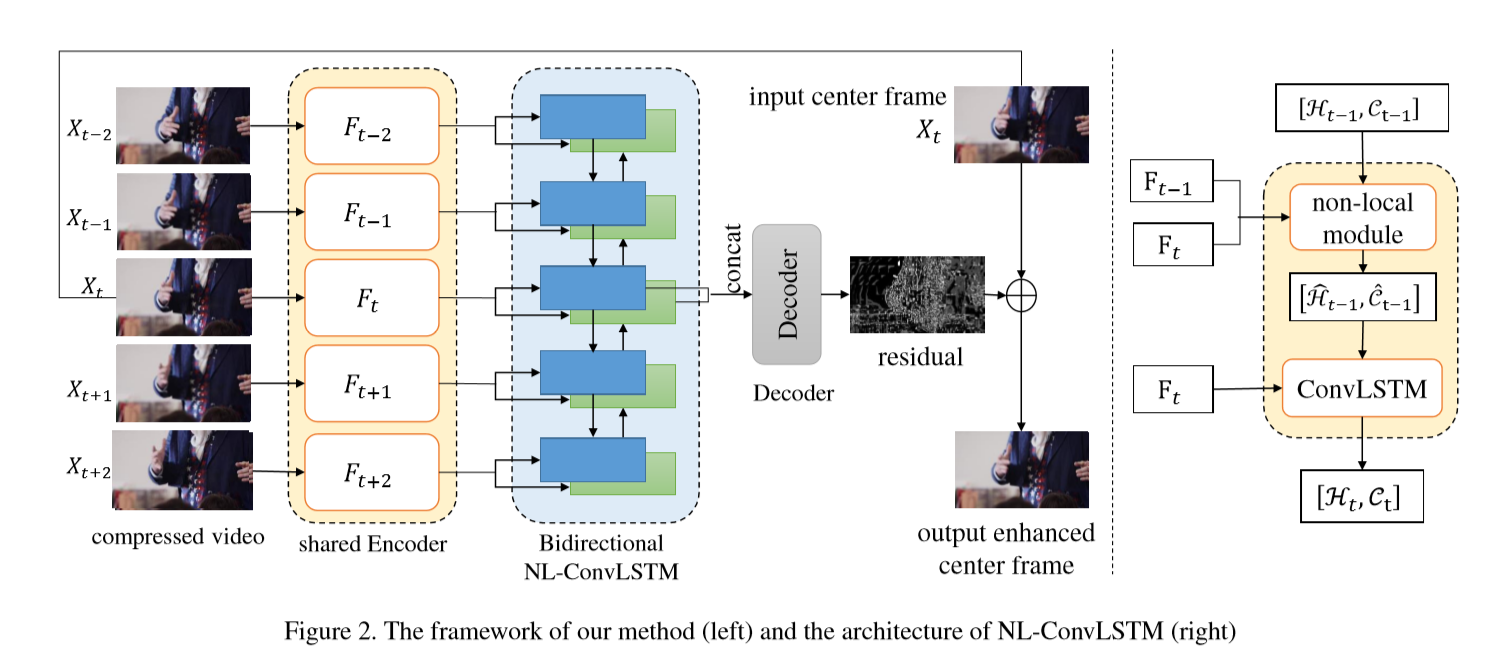
解码器。将NL-ConvLSTM模块两个方向的隐藏状态解码为残差，重构出高质量的帧。具体来说，我们首先通过一个kernel size为1×1的convolutional layer来合并这些hidden state，然后使用几个堆叠的convolutional layers来产生残差。

3.2 Non-local ConvLSTM

ConvLSTM可以描述为如下[37]:

\[\left[\mathcal{H}_{t}, \mathcal{C}_{t}\right]=\operatorname{ConvLSTM}\left(F_{t},\left[\mathcal{H}_{t-1}, \mathcal{C}_{t-1}\right]\right) \]

为了学习鲁棒的时空相关性，我们将非局部机制引入到ConvLSTM中来帮助估计帧序列中的运动模式。作为ConvLSTM的延伸，NL-ConvLSTM可以表示为：

\[\begin{aligned} S_{t} &=N L\left(F_{t-1}, F_{t}\right) \\\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] &=N L W \operatorname{arp}\left(\left[\mathcal{H}_{t-1}, \mathcal{C}_{t-1}\right], S_{t}\right) \\\left[H_{t}, C_{t}\right] &=\operatorname{Conv} L S T M\left(F_{t},\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right]\right) \end{aligned} \]

\(S_{t} \in \mathbb{R}^{N \times N}\)表示当前帧的像素与前一帧的所有像素之间的相似性矩阵。NL是计算两帧特征间相似矩阵的非局部算子，NLWarp是对t-1时刻的隐状态和单元状态进行加权和运算。
在非局部操作[3]之后，我们工作中的帧间像素相似度和非局部warping操作如下:

\[\begin{aligned} D_{t}(i, j) &=\left\|F_{t-1}(i)-F_{t}(j)\right\|_{2} \\ S_{t}(i, j) &=\frac{\exp \left(-D_{t}(i, j) / \beta\right)}{\sum_{\forall i} \exp \left(-D_{t}(i, j) / \beta\right)} \\\left[\hat{\mathcal{H}}_{t-1}, \hat{\mathcal{C}}_{t-1}\right] &=\left[\mathcal{H}_{t} \cdot S_{t}, \mathcal{C}_{t} \cdot S_{t}\right] \end{aligned} \]

\(i, j \in\{1, \cdots, N\}\)为特征图中像素的索引,\(F(i)\) 和\(\mathcal{H}(i)\)是位置\(i\)处的对应的特征和状态。\(D_{t}(i, j)\) 和 \(S_{t}(i, j)\)为t-1时刻前一特征图中像素i与t时刻当前特征图中像素j在所有通道上的欧氏距离和相似度。\(S_{t}(i, j)\)满足\(\sum_{i} S_{t}(i, j)=1\)，因此，非局部方法可以看作是一种特殊的注意机制[39]。

3.3. Two-stage Non-local Similarity Approximation

对于高分辨率的视频，直接计算\(S_{t} \in \mathbb{R}^{N \times N}\)，并且进行warping操作，会产生极高的计算量和内存开销。因此,我们提出一个两阶段的non-local方法近似\(D_{t}\)为\(\hat{D}_{t}\)，近似\(S_{t}\)为\(\hat{S}_{t}\)，在保证精度的同时，减少了计算量和内存。我们的近似方法的核心思想是根据编码器学习到的深度特征对图像块进行预滤波，然后再计算像素级的相似度。详情如下:

在第一阶段，我们使用平均池从编码器中提取feature map，并减少几何变换(移位和旋转)的块匹配灵敏度。表示平均池化的核大小为\(p\)，下采样特征图为\(F_{t}^{p}\)。然后将feature map的分辨率降低到\(N / p^{2}\)，即，为原分辨率的\(1 / p^{2}\)。下采样特征图\(F_{t}^{p}\)的每个超像素对应于原始特征图中的\(p^{2}\)像素块。因此，向下采样的距离矩阵\(D_{t}^{p} \in \mathbb{R}^{\left(N / p^{2}\right)^{2}}\)可以通过下面这个式子计算：

\[D_{t}^{p}(i, j)=\left\|F_{t-1}^{p}(i)-F_{t}^{p}(j)\right\|_{2}$$. For each pixel in any block $b_{t}$ of $F_{t}^{p}$ , we consider only $k*p^{2}$ pixels in the $k$ blocks of $F_{t}^{p}$ that are nearest to $b_{t}$. 在第二阶段，我们计算并存储$F_{t}$的每个像素与$F_{t-1}$对应的$k \times p^{2}$像素之间的相似性。而其他像素在前面的帧,$\hat{D}_{t}$元素和$\hat{S}_{t}$分别设置为$+\infty$和$0$。由于相似像素是稀疏的，一个像素可以由相邻帧的几个像素来表示，所以top-$k$块近似的质量损失可以忽略不计。图3展示了两阶段相似度近似的工作流程。$\mathcal{C}_{t}$的NLWarp操作与$\mathcal{H}_{t}$相似。为了简单起见，我们在图3中只显示了$\mathcal{H}_{t}$的操作。  （后面还有复杂度分析，non-local与运动补偿的比较，以及实验，这是大佬对这篇文章的看法https://www.cnblogs.com/RyanXing/p/11924219.html，看了之后发现这篇文章自己并没有看太懂，特别是加速non-local。实验和总结也很重要，慢慢来）\]