二分查找

一：二分查找算法

本文章列出刷题中常用的二分查找场景：寻找一个数、寻找左侧边界、寻找右侧边界。 ps：什么最大值的最小，最远的最近。->都是二分

1:1二分查找框架

int binarySearch(int[] nums, int key) {
    int left = 0, right = ...;

    while(...) {
        int mid = (right + left) / 2;
        if (nums[mid] == key) {
            ...
        } else if (nums[mid] < key) {
            left = ...
        } else if (nums[mid] > key) {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节.

但是元素必须是有序的建议  

建议计算mid防止溢出

 mid = (l + r + 1) / 2;

 

1.2寻找一个数 

搜索一个数，如果存在，返回其索引，否则返回 -1。

    public class BinarySearch
    {
        public static int bs(List<int> data, int key)
        {
            int low = 0, mid = 0;
            int high = data.Count - 1;
            while (low <= high)
            {
                mid = (low + high) / 2;
                if (data[mid] == key)
                {
                    return mid;
                }
                else if (data[mid] > key)
                {
                    high = mid - 1;
                }
                else if (data[mid] < key)
                {
                    low = mid + 1;
                }
            }
            return -1;
        }
    }

一个有顺序的数组,我要找一个东西,我直接切一半,我要找的小了我就往左跑,大了我就往右跑，重复....。

   PS：最差的情景 比较次数是:Log2(n+1),这个是运气真的差.且期望时间复杂度是O(Log2n).很惨

   一种是两端都闭的区间,一种是只闭一端的区间，问题点 如果索引大小为length是越界的，上述代码为两端都闭的区间

   显而易见调出条件为找到目标值就可以终止

   if (data[mid] == key)
   {
        return mid;
   }

 如果没找到，就需要 while 循环终止，然后返回 -1 

  当前是当前集合或者数组内没有搜索的数字

   1： while(left <= right) 的终止条件公式则为  [last,last-1], 例如：10000 ，9999 你的搜索区间直接为空，但此时while直接就终止了。因为你的搜索空间只有1，可见这时候搜索区间为空，没有数字即>=1000 又<=9999。所以while终止

   2：另外一种情况,你写个left < right ，公式则为[last,last]，如10000,10000，直接没有搜索区间，只有一个10000，这个区间[10000,10000]，不会被搜索,这个索引[10000]没有被搜索的，这样你就写了bug -->

 return  nums[first] == key? first: -1;

 

1.3 寻找边界的二分搜索

1.3.1 寻找右边界的二分搜索

再次强调：二分的最终的一个目的就是删掉不存在答案的区间。

如图：如果这个我要找 满足包含（可以理解为>=4）4的值 ，这种情况可以抽象为一个模型,满足的都为1，不满足的都为0. 只要找到第一个就是答案

 

 

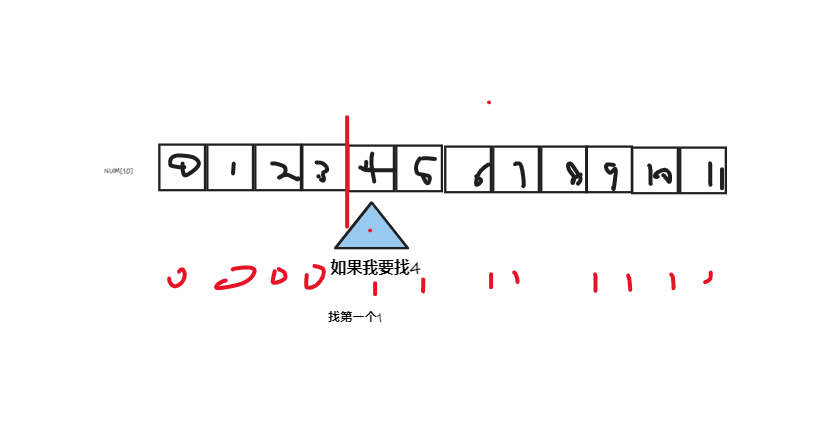
先初始化好两边的左右区间 ,现在需要变化一下while 的初始条件，

while(L!=R){
   int mid=（L+R）/2;
   L=mid+1
   R=mid
}

注解：

 

 

 

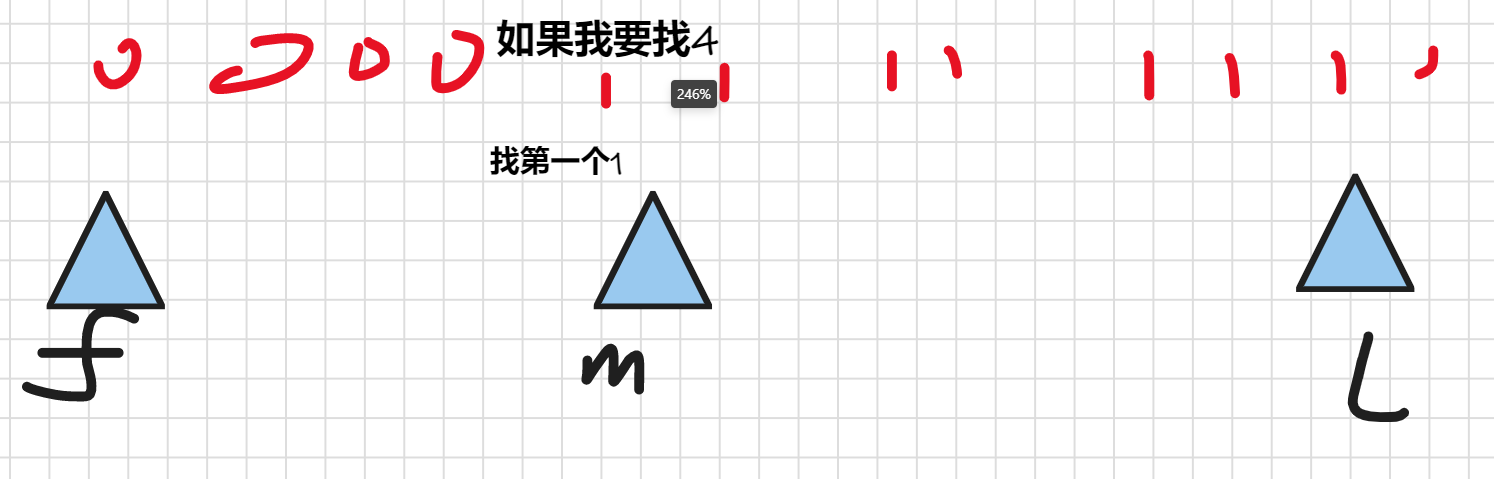
 这样看图你的右边一定都是1， 所以应该动的是last 指针 让他指过来

   有一种可能是 mid 也是可能是答案的，所以这个mid就不能删，所以Last 指针直接指mid，只删掉一定不存在答案的区间->所以动last指针，

为什么你指向的first->是+1

   如果循环在跑一次你的mid就指向了0了，而左边都是0，一定不是答案，所以first=first+1.

   结论是：左右指针重合时，就是第一个1

 

1.1.2 ：寻找左侧边界的二分搜索

 

 

 

 如上文得出的模型,与上文相反，这个是需要找最后一个1.

while（L!=R）{
   int mid =(L+R+1)/2；
   L=mid；
   R=mid-1；
}

 

 

 

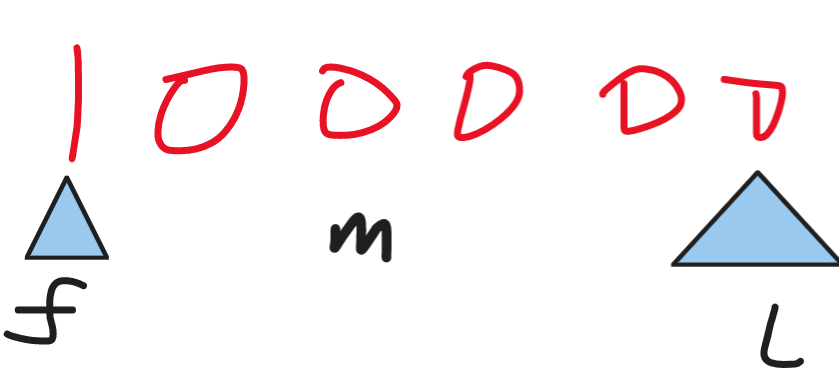
如果mid指向了1，则左边都是1。同理这个mid 也可能是最终答案，不能删除。

下次循环时L指向了这个mid，此时在求出一个mid,则应该动右边的指针。

 

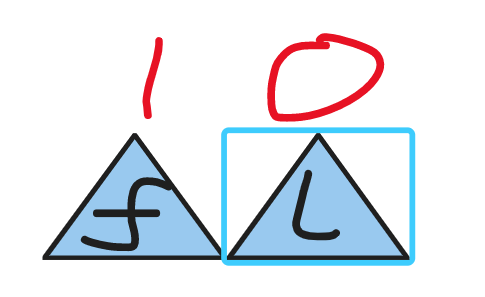
多次循环最终形成了这个样子，则在需要求一个mid =（f+l）/ 2  则 指向了左指针也就指向了mid,如果在动左指针，左指针还此处。 （现在就死循环了）

为了避免这个事情，提前给它+1，当遇到上文死循环时,则他就会指向了右边（L），而且右边一定不是答案，而L(R)=mid-1 又回到了F(F)这里.

此时左右重合就找了答案

 

下个目标为 斐波那契查找和 插值查找