后缀自动机
后缀自动机
初学建议看这个 基本上是最好的中文资料了。
字符串的SAM是一个dAg,它的边上会有一个字符,从根节点走到终止节点会构成一个后缀。它可以且只可以接受 $ s $ 的所有后缀,并且满足可以接受 $ s $ 的后缀的自动机中,SAM是节点最少的。
由于后缀自动机是个dAg,它的每个节点代表的是一些字符串(因为并不只有一条路可以到达)。
-
定义 : endpos 集合
对于一个 $ s $ 的非空子串 $ t $ ,endpos(t) 表示 $ s $ 中出现的所有 $ t $ 的结束位置。
-
定义:endpos 等价类
如果两个字串 $ t_1 $ , $ t_2 $ 的 endpos 集合相等,那么称他们在一个 $ endpos $ 等价类。
那么所有字串都可以被分成很多的 endpos 等价类。最终构建SAM后其实所有除了根的点就代表了一个 endpos 的等价类,SAM的点数其实就是 endpos 等价类的数量+1。
前面说过,再DAG上一个点代表了一些字符串,这些字符串是通过不同路径走到这个点生成的,而这些字符串就属于一个 endpos 等价类。
-
引理1:字符串的两个非空子串 $ u,v(|u|\leq|v|) $ 如果他们的 endpos 等价类相等那么可以推出 $ u $ 是 $ v $ 的字串。
这个证明比较显然的。
同时可以有 若 $ u , v $ endpos 集合相同且 $ |u|=|v| $ 那么
-
引理2:字符串的两个非空字串 $ u,v $ 它们的 endpos 集合要么互相包含,要么没有交。
而这两种情况取决于它们是否有子串关系。
并且有 如果 $ u $ 是 $ v $ 后缀,那么 $ endpos(u) \sube endpos(v) $ 比较显然。
-
引理3:把一个 endpos 等价类的串从长到短排序,那么长度一定是连续的。
也比较显然吧,证明就不写了。
我们知道了, SAM 的每一个节点代表的是一个 endpos 等价类,包含了很多串。由前面的引理我们也知道,它的所有串的长度是连续的。现在,我们定义一个点的后缀连接 link ,$ link(u) $ 连接向一个 endpos 等价类,这个等价类包含了最长的串 $ t $ 使得 $ t $ 是 $ u $ 中最短串的子串,并且它的 endpos 集合和这个点的 endpos 集合不同。如果我们认为 $ len(u) $ 为 $ u $ 节点的最长的串的长度,$ minlen(u) $ 表示 $ u $ 节点最短串的长度,且 $ t $ 所在的等价类对应的节点是 $ f $ 那么 $ len(f) + 1 = minlen(u) $。
同时为了方便,我们认为 $ t_0 $ 也就是根节点,它的 endpos 集合是全集,规定为 $ {0,1,\dots,|S|} $
-
引理4:所有后缀连接形成一棵树
显然。
-
引理5:后缀连接形成的树上,儿子节点的 endpos 被父亲的 endpos 包含,并且一个节点的儿子们没有交集。
首先,包含很容易想到,因为父亲的串是儿子的后缀,由引理 2 就知道了。
没有交集的话,假设一对兄弟由交集,那么它们必然由 endpos 集合的包含关系,也就是互为后缀(引理2)。假设 $ u , v $ 为 $ f $ 的儿子,$ u $ 是 $ v $ 的后缀,我们知道它们的等价类不同,但是 $ u $ 是 $ f $ 的儿子,意味着它比 $ f $ 长那么根据 link 的定义 $ v $ 必然会连接向节点 $ u $,而不是节点 $ f $ 。
后缀连接形成的树叫做 parent tree 。而 parent tree 的实质是一棵前缀树。
同时我们有 $ v $ 开始往上沿着 link 跳,得到的所有 串 的的长度组成的集合是 $ [0,len[v]] $ 。
构造SAM
SAM的构造同样采用增量法。
我们假设根节点是 $ t_0 $ ,添加一个字符 $ c $ ,我们添加一个点在最后,我们需要知道的是它的 link , son , 以及哪些点可以通过 $ c $ 转移到它。
-
我们记录添加前,整个串所代表的节点位置是 $ last $ 。
-
现在我们创建一个节点 $ cur $ 并且让 $ len(cur) = len(last) + 1 $ 。这个时候我们并没有确定 $ link(cur) $。
-
考虑怎么确定其他点向这个点的 son 的关系。原来可以转移到 $ last $ 的某一个后缀的所有转移,都可以通过添加字符 $ c $ 转移到 $ cur $ 。我们开始从 last 向上跳,记录当前跳到的节点是 $ p $ ,如果 $ p $ 没有向 $ c $ 的转移,那么我们添加从 $ p $ 向 $ c $ 的转移到 $ cur $ 。一直跳直到当前节点拥有向 $ c $ 的转移或者到达了根。假如我们顺利跳到了根节点,就意味着字符串中没有出现过添加 $ c $ 后字符串的后缀,也就是没有出现过字符 $ c $ (因为出现过 $ c $ 那么 $ c $ 就是字符串的后缀)。这种情况我们可以直接把 $ cur $ 的 link 指向根。
-
假设当前节点是 $ p $ ,它拥有向 $ c $ 的转移,假设 $ p $ 向 $ c $ 转移到了 $ q $ ,我们分两种情况来做:
-
$ len(q) = len(p) + 1 $ 这种情况下, $ q $ 上的最长的也只是 $ p $ 上最长的添加了一个 $ c $ 得到的后缀,我们就知道当前整个串的最长后缀就是 $ len(q)+1 $。因为 $ p $ 是第一个跳到的节点,是第一个添加 $ c $ 后仍然存在于字符串中的节点。又 $ len(p) + 1 = len(q) $ 所以 $ q $ 就是 $ cur $ 连向的点。
-
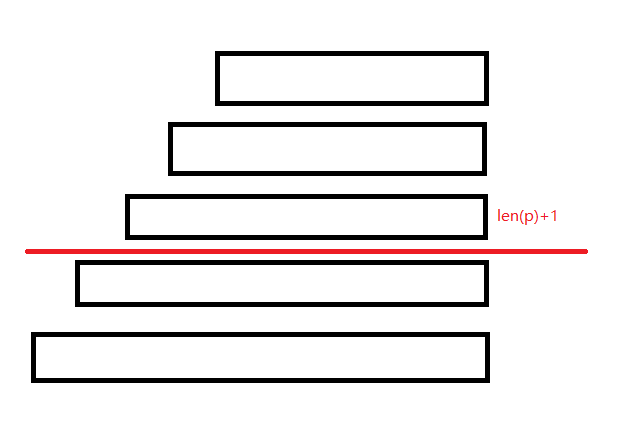
否则,$ len(q) > len(p) + 1 $ 这种情况下, $ q $ 上最长的必然不是 $ cur $ 的后缀。因为长度大于了 $ len(p)+1 $ 而 $ len(p)+1 $ 必然是当前整个串最长的后缀,我们可以把这个节点拆开,像这样:
![_D2QQ2BWXII__VL_G6VJR5B.png]()
上面这一段表示的点就是 $ link(cur) $ 指向的位置。它的 endpos 等价类又添加了一个新的位置(结尾),包含了下面这一些后缀表示的节点,显然就有下面这些后缀组成的点的 link 就是上面这一段。
同时我们需要继续从 $ p $ 跳 link 把原来指向 $ q $ 的点指向 cut 开的上面那一段组成的点。
-
-
别忘了更新 $ last $
代码丢在最后的。先来写另一个重要的东西:
SAM + 线段树合并
这是一种常用的套路今天学了一下。
有时我们需要一个 SAM 上一个节点的 endpos 集合。这个时候可以先把每个结束位置对应节点的 pos 设置为这个位置(用权值线段树存)。然后就 dfs 一下,合并线段树就好了。
那么这样复杂度为啥是对的呢,考虑一个点的所有儿子的 endpos 集合是没有交集的,因此总的线段树叶子个数是不会超过 2n 的,总空间复杂度是 $ O(nlogn) $
例题没意外应该会写的(🐦💨💨)。
写了。。在这里
- NOI 2018 你的名字
广义 SAM
如果要严谨的证明建议看 2015 年的论文。
大概就是对 Trie 来建 SAM 。
对于一个串,它的 endpos 集合是 Trie 上的所有点,满足对于这些点存在一个祖先,使得从祖先到这个点的路径连起来是这个串。和普通字符串上的 endpos 集合定义是很像的。
然后广义 SAM 上一个节点仍然表示一个 endpos 等价类,后缀链接连向的是最长的后缀使得它的 endpos 和这个点上的点不一样。其实是和 SAM 很类似的啦。
说一下广义SAM的构建:
-
最简单轻松的,如果只是插入一些字符串,那么插入一个后把 last 设置为根就好了。
据说这种构造在某些时候是会死掉的
但是好写啊,如果单词重复据说会加多点。。但是平时写由于很难出错一直写的这个。 -
标准的,对于所有串构造一棵 Trie 然后 BFS 这个 Trie 来构造。加入一个点的时候就把 last 设置为它父亲加入完时的 last。
注意,写 DFS 是会被卡的!可以看这篇博客
广义SAM的复杂度和 SAM 类似,节点数也是 2n 的啦。。具体内容见论文。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
#define MAXN 2000006
int n , lst;
char ch[MAXN];
ll ans = 0;
struct SAM{
int son[MAXN][27]; // sons
int par[MAXN] , len[MAXN]; // node
int head[MAXN] , nxt[MAXN<<1] , to[MAXN<<1]; // edge
int cnt , ecnt;
int sz[MAXN];
void adde( int u , int v ) {
to[++ecnt] = v;
nxt[ecnt] = head[u];
head[u] = ecnt;
}
void init( ) {
memset( son , 0 , sizeof son ) , memset( head , -1 , sizeof head );
cnt = lst = 1; ecnt = 0;
}
void addall( ) { // 将所有link边连到边集合中
for( int i = 2 ; i <= cnt ; ++ i ) adde( par[i] , i );
}
void ins( int x ) {
int cur = ++ cnt;
len[cur] = len[lst] + 1 , sz[cur] = 1;
int p = lst;
while( p && !son[p][x] ) son[p][x] = cur , p = par[p];
if( !p ) par[cur] = 1;
else {
int q = son[p][x];
if( len[q] == len[p] + 1 ) par[cur] = q;
else {
int cl = ++ cnt;
memcpy( son[cl] , son[q] , sizeof son[q] );
par[cl] = par[q]; // copy
len[cl] = len[p] + 1 , par[q] = par[cur] = cl;
for( ; son[p][x] == q ; p = par[p] ) son[p][x] = cl;
}
}
lst = cur;
}
void dfs( int cur ) {
for( int i = head[cur] ; ~i ; i = nxt[i] ) {
int v = to[i];
dfs( v );
sz[cur] += sz[v];
}
if( sz[cur] > 1 ) ans = max( ans , 1LL * sz[cur] * len[cur] );
}
} S ;
int main() {
S.init();
scanf("%s",ch); n = strlen( ch );
for( int i = 0 ; i < n ; ++ i )
S.ins( ch[i] - 'a' );
S.addall( );
S.dfs( 1 );
cout << ans << endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号