10.23 模拟赛
10.23 模拟赛
dls 毒瘤！
T1 爬杆
首先，50分很好做，单调栈找找就行了。。后面做法考场胡了个错误的贪心（Orz zzh 会正解）
每个点到全局最小点都得有路。我们可以考虑拿最小点出来递归左右（其实就是笛卡尔树）。
然后还有一个贪心，对于两个点我们想在其中修路，假设小的在左边，大的在右边，那么一定是小的走一段，剩下的都走大的，显然最优。其实第一段之间是不会有其他点的，所以可以看成是全部走的大的。
一个生动形象的例子，如果我们向从第一个梯子到最后一个得到一条路，那么可以这么修：
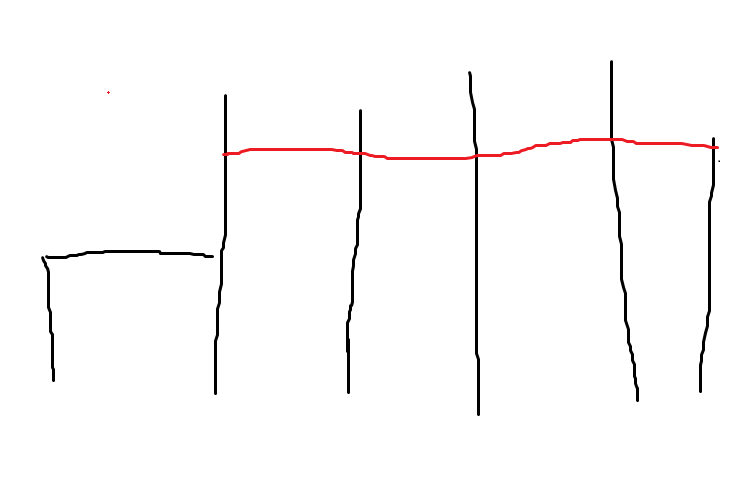
如果到达一个点，发现假设左边原本就搭建了高度 $ h_l $ 的梯子，那么递归时考虑如果 $ h_l = a_i $ 那么显然递归时不需要再修建新的梯子，否则都需要。 右边同理。
相当于存了笛卡尔树的板子了
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<stack>
using namespace std;
#define pii pair<int,int>
#define mp make_pair
#define int long long
#define MAXN 200006
#define MAXV 1000006
int n , mx;
int h[MAXN] , stk[MAXN] , top = 0;
int L[MAXN] , R[MAXN];
int T[MAXV << 2];
int que( int rt , int l , int r , int L , int R ) {
if( L <= l && R >= r ) return T[rt];
int m = l + r >> 1 , ret = -0x3f3f3f3f;
if( L <= m ) ret = max( ret , que( rt << 1 , l , m , L , R ) );
if( R > m ) ret = max( ret , que( rt << 1 | 1 , m + 1 , r , L , R ) );
return ret;
}
void mdfy( int rt , int l , int r , int p , int c ) {
T[rt] = max( T[rt] , c );
if( l == r ) return;
int m = l + r >> 1;
if( p <= m ) mdfy( rt << 1 , l , m , p , c );
else mdfy( rt << 1 | 1 , m + 1 , r , p , c );
}
int S[MAXN] , len[MAXN];
namespace solve2 {
int l[MAXN] , r[MAXN] , d[MAXN] , rt , stk[MAXN] , tp = 0;
bool cmp( int x , int y ) {
return h[x] < h[y];
}
void build(){
for( int i = 1 ; i <= n ; ++ i ) {
int k=tp;
while (k > 0 && h[stk[k-1]] > h[i]) --k;
if (k) r[stk[k-1]]=i;
if (k<tp) l[i]=stk[k];
stk[k++]=i;
tp=k;
}
}
int res(0);
void dfs( int u , int ll , int rr ) {
if( l[u] )
if( h[u] == ll ) dfs( l[u] , ll , ll );
else res += u - l[u] , dfs( l[u] , ll , h[l[u]] );
if( r[u] )
if( h[u] == rr ) dfs( r[u] , rr , rr );
else res += r[u] - u , dfs( r[u] , h[r[u]] , rr );
}
int main() {
build();
dfs( stk[0] , -1 , -1 );
return res;
}
}
int tt;
signed main() {
cin >> n;
for( int i = 1 ; i <= n ; ++ i ) scanf("%lld",&h[i]) , mx = max( mx , h[i] ) , S[i] = S[i - 1] + h[i];
cin >> tt;
for( int i = 0 ; i <= mx * 4 + 3 ; ++ i ) T[i] = -0x3f3f3f3f;
for( int i = 1 ; i <= n ; ++ i ) {
int t = que( 1 , 1 , mx , 1 , h[i] );
L[i] = t;
mdfy( 1 , 1 , mx , h[i] , i );
}
int ans = 0;
for( int i = 1 ; i <= n ; ++ i )
if( L[i] != -0x3f3f3f3f )
len[i] = len[L[i]] + ( h[i] - h[L[i]] ) * L[i] + S[i - 1] - S[L[i]] - ( i - 1 - L[i] ) * h[i] , ans += len[i] , ans += i * ( n - i );
else
len[i] = S[i] - h[i] * i , ans += len[i] , ans += i * ( n - i );
cout << ans << ' ';
if( tt == 1 ) return 0;
cout << solve2::main() << endl;
}
T2 变换
可以发现答案就是 不是 k 的数量 + 大于k小于k的连续段的长度/2的和
然后写代码是不可能写代码的这辈子不可能写代码的。
duliu!
T3 游戏
满足条件的情况一定是原树存在完美匹配。如果有点到子孙或者子孙到祖先的完美匹配，先手选择了一个位置，后手一定可以选择一个和它匹配的位置。否则在几次选择后先手必胜，因为无法完美匹配。
然后考虑设 $ dp[i][j] $ 表示 i 为根子树中有 j 个点还没有被匹配的情况数，就可以直接转移了。考虑根节点是否被选择，被选择其实就是 $ dp[i][j] = dp[i][j] + dp[i][j + 1] $
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
using namespace std;
#define int long long
#define MAXN 2006
#define P 998244353
int n;
int dp[MAXN][MAXN];
vector<int> G[MAXN];
int siz[MAXN];
void dfs( int u , int fa ) {
dp[u][0] = 1 , siz[u] = 1;
for( int v : G[u] ) {
if( v == fa ) continue;
dfs( v , u );
siz[u] += siz[v];
for( int j = siz[u] ; j >= 0 ; -- j ) {
dp[u][j] *= dp[v][0] , dp[u][j] %= P;
for( int k = 1 ; k <= siz[v] && j - k >= 0 ; ++ k )
dp[u][j] += dp[v][k] * dp[u][j - k] % P , dp[u][j] %= P;
}
}
int tt = dp[u][0];
for( int i = 0 ; i < siz[u] ; ++ i ) dp[u][i] += dp[u][i + 1] , dp[u][i] %= P;
dp[u][1] += tt;
}
signed main() {
cin >> n;
for( int i = 1 , u , v ; i < n ; ++ i )
scanf("%lld%lld",&u,&v) , G[u].push_back( v ) , G[v].push_back( u );
dfs( 1 , 1 );
int res = 0;
for( int i = 1 ; i <= n ; ++ i ) res += dp[1][i] , res %= P;
cout << res << endl;
}
