二叉树

一、基本概念

二叉树的性质：
性质1：一棵非空二叉树的第i层上至多有2^i-1个结点（i>1）。

性质2：深度为h的二叉树至多有2^h-1个结点（h>1）。

（证明）：根据性质1，二叉树中所有节点数为2⁰+2¹+...+2^h-1=2^h-1

性质3：对于任意一棵二叉树，如果其叶子结点数为n₀，度为2的结点数为n₂，则n₀=n₂+1。

（证明）：二叉树中所有结点数为：n=n₀+n₁+n₂ 。二叉树中有n-1条边，这些边由度为1和2的结点产生，即n-1=n1+2*n2，即n0+n1+n2=n1+2*n2+1，即n₀=n2+1。

满二叉树：

所有叶子结点位于同一层，其它非叶子结点的度为2。若满二叉树的深度为h，则其所有结点数必为：2^h-1。

 

 完全二叉树：

扣除最大层次那层后即成为一棵满二叉树，且层次最大那层的所有结点均向左靠齐。

 

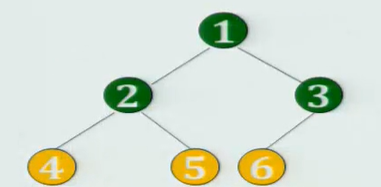
完全二叉树的性质：若完全二叉树有n个结点，按照从上到下，从左往右的顺序，从1开始，给每个结点编号，对于编号为i的结点有：

（1）如果i>1，则序号为i的结点的双亲结点为：i/2取整。（如2，3结点的双亲结点都为1）；如果i=1，则结点i为根节点。

（2）如果2i>n，则结点i无左子女（此时结点i为叶子节点）；若2i<=n，则其左子女为2i。

（3）如果2i+1>n，则结点i无右子女；若2i+1<=n，则其右子女为2i+1。

 二、二叉树的存储结构

1.顺序存储

将各结点通过编号后，存入数组中。

 

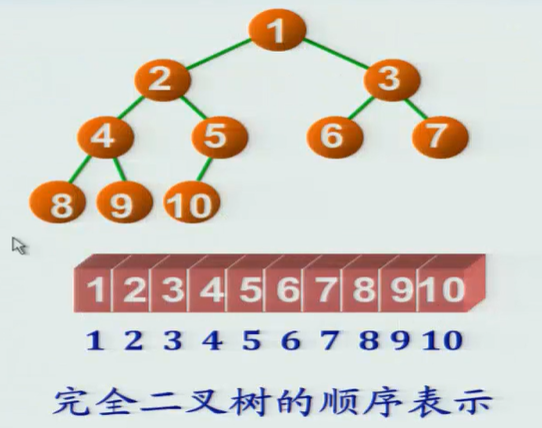
 顺序存储结构代码实现：

typedef Maxsize 100
typedef char datatype;
typedef struct{
    datatype data;
    int lchild,rchild;
}node;
node tree[Maxsize];
int n;
int root;

 

2.链式存储

每个结点包含三个域，分别用指针记录该结点的属性值，及左右子树的位置。

 

 

 

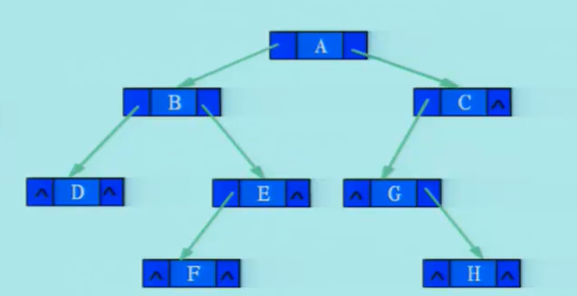
 链式存储结构代码实现：

typedef char datatype;
typedef struct node{
    datatype data;
    struct node*lchild,*rchild;
}bintnode;
typedef bintnode *bintree;

 

三、二叉树的创建

使用createbintree()函数创建二叉树，使用链式存储结构。按照前序遍历的顺序输入二叉树各结点值，遇到空结点使使用#代替。

（例子：ab##c##）

 

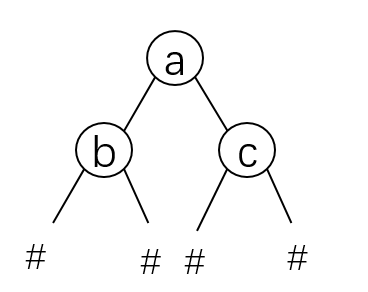
 前序遍历顺序创建二叉树代码实现：

bintree createbintree(){
    char ch;
    bintree t;
    if((ch=getchar())=='#')
        t=NULL;
    else{
        t=(bintree)malloc(sizeof(bintnode));
        t->data=ch;
        t->lchild=createbintree();
        t->rchild=createbintree();
    }
    return t;
} 

 

四、二叉树的遍历

1.递归遍历

递归前序遍历：

void preorder(bintree t){
    if(t){
        printf("%c ",t->data);
        preorder(t->lchild);
        preorder(t->rchild);
    }
}

 

递归中序遍历：

void inorder(bintree t){
    if(t){
        inorder(t->lchild);
        printf("%c ",t->data);
        inorder(t->rchild);
    }
}

 

递归后续遍历：

void postorder(bintree t){
    if(t){
        postorder(t->lchild);
        postorder(t->rchild);
        printf("%c ",t->data);
    }
}

 

2.非递归遍历

在采用非递归实现时，需用一个栈来记录回溯点。

/* 用于遍历的栈 */
typedef struct {
    bintree data[100];
    int tag [100]; 
    int top;
}sequence_stack;

/* 入栈操作 */
void push(sequence_stack *s,bintree t){
    s->data[s->top]=t;
    s->top++; 
}

/* 出栈操作，取栈顶元素 */
bintree pop(sequence_stack *s){
    if(s->top!=0){
        s->top--;
        return (s->data[s->top]);
    }
    else
        return NULL;
}

 

非递归前序遍历：

void preorder(bintree t){
    printf("前序遍历：");
    sequence_stack s;
    s.top=0;
    while((t) || (s.top!=0)){
        if(t){
            printf("%c ",t->data);
            push(&s,t);
            t=t->lchild;
        }
        else{
            t=pop(&s);
            t=t->rchild;
        }
    }
}

 

非递归中序遍历：

void inorder(bintree t){
    printf("中序遍历：");
    sequence_stack s;
    s.top=0;
    while((t) || (s.top!=0)){
        if(t){
            
            push(&s,t);
            t=t->lchild;
        }
        else{
            t=pop(&s);
            printf("%c ",t->data);
            t=t->rchild;
        }
    }
} 

 

 

φ(゜▽゜*)♪ 感谢观看，希望对你有帮助！