树

一、树的基本概念

结点：树上的每个结点。

结点的度：该结点的分支的个数。（如A的度是3，B的度是2）

树的度：树中所有结点的度的最大值。

叶子结点：度为0的结点。

分支结点：度大于0的结点。

结点的层次：假设根结点为第一层，则A为第一层，BCD为第二层。

树的深度：树中叶子结点所在的最大层次。

森林：是m（m>=0）棵互不相交的树的集合。

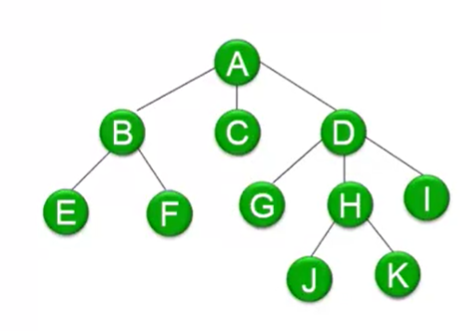
树的表示方法：

（1）括号表示法：子树在结点后面的括号中。如：A(B(E,F),C,D(G,H(J,K),I))

（2）嵌套集合表示法

 

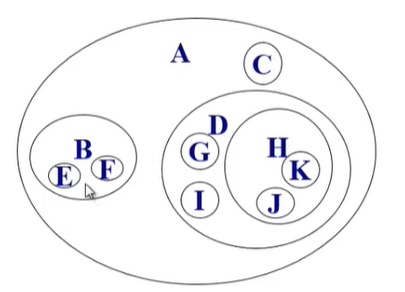
（3）凹入表示法

 

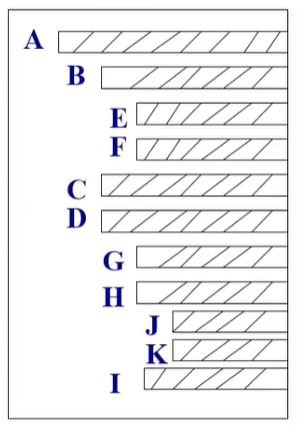
二、树的存储结构

1.双亲表示法

每个结点包含两部分信息：结点值data和双亲结点parent。

 

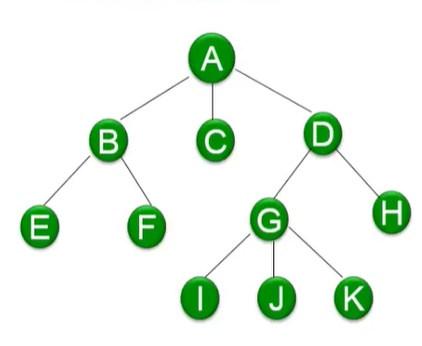
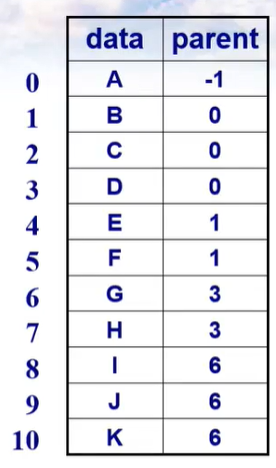
实现代码：

#define Maxsize 100
typedef char datatype //结点值类型 
typedef struct node{  //结点结构体 
    datatype data;
    int parent； 
}node;
typedef struct tree{  //树的结构体 
    node treelist[Maxsize];
    int length,root;
}tree; 

 

2.孩子表示法

 采用孩子表示法时，树中的每个结点包含两部分信息：自身的值，其所有子女的位置。

根据子女位置的实现方式不同，又可分为三种方法表示孩子结点：（1）指针，（2）数组，（3）链表。

 

2.1指针方式的孩子表示法

结点包含两个域：

（1）结点值data

（2）指针数组，数组中每个指针均为指向该结点子女的指针。

 

 

 

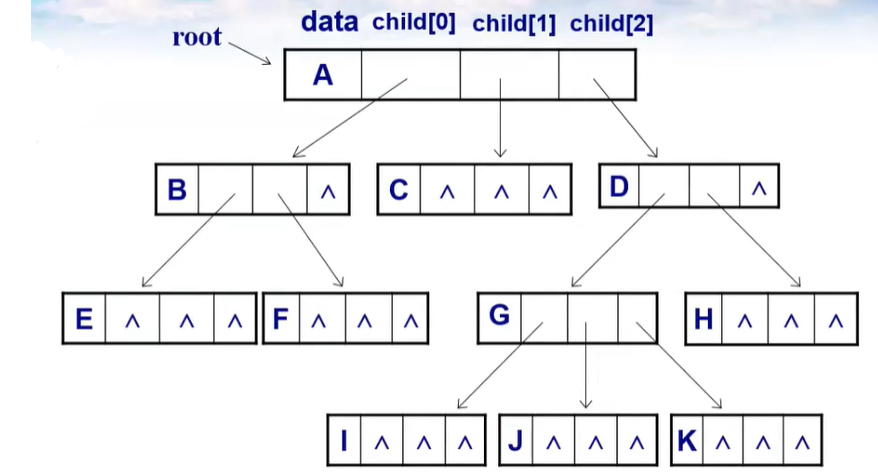
2.2数组方式的孩子表示方法

 

 代码实现：

#define m 3
#define Maxsize 20
typedef char datatype //结点值类型 
typedef struct node{  //结点结构体 
    datatype data;
    int child[m]； 
}node;
node tree[Maxsize];  //树 
int root;
int length;

 

2.3链式方式的孩子表示法

把每个结点的子女排列起来形成一个单链表，这样，n个结点就有n个单链表，再用数组将这n个单链表存储。

 

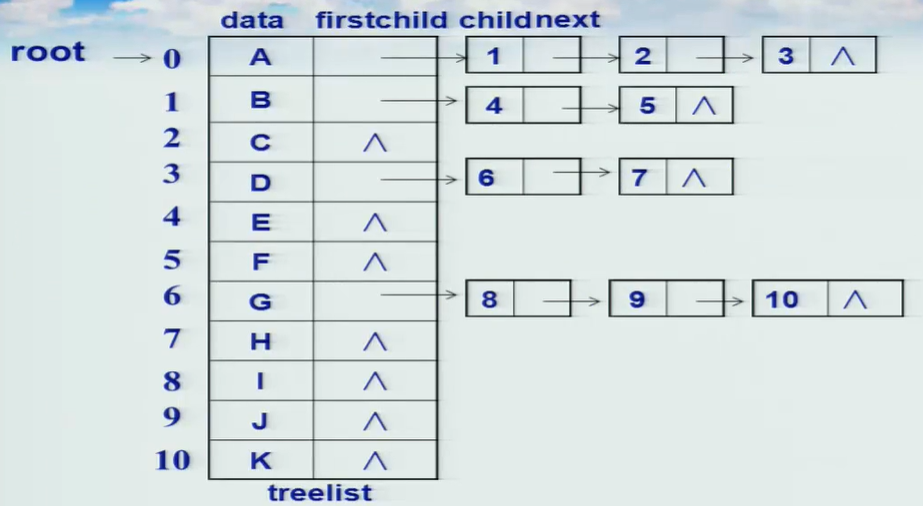
 代码实现：

#define Maxsize 100
typedef char datatype //结点值类型 
typedef struct chnode{  //结点后的链表 
    int child;        //结点下标 
    struct chnode*next 
}chnode;
typedef chnode* chpoint;

typedef struct {    //树中的每个结点 
    datatype data;
    chpoint firstchild;
}node; 

typedef struct{     //存放结点的数组 
    node treelist[Maxsize];
    int length,root;
}tree; 

 

3.孩子兄弟表示法（二叉树表示法）

在存储树中每个结点时，除了包含该结点值，还设置两个指针firstchild和rightsibling，分别指向该结点的第一个子女和其右兄弟，即二叉链表方式加以存储，因此该方法也被称为二叉树表示法

 

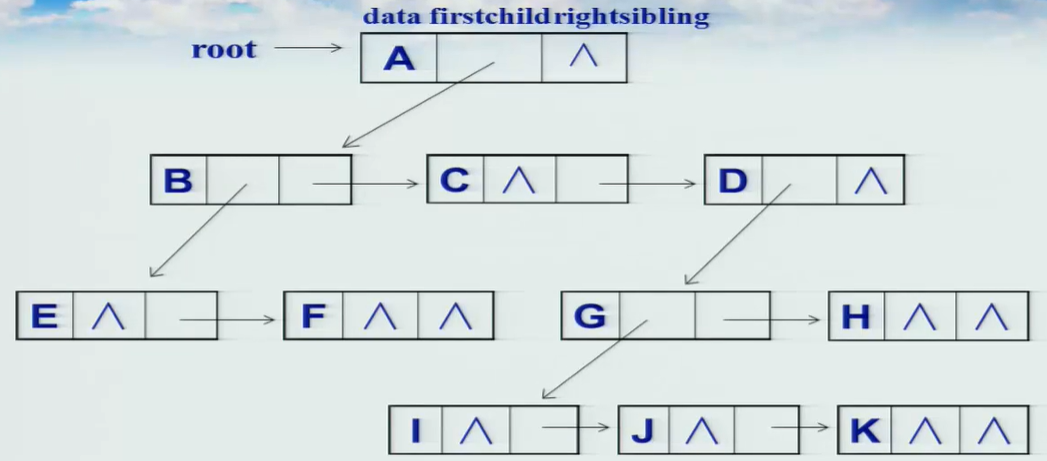
三、树的创建

 按照前序遍历的顺序，通过递归调用创建一棵度为3的树。

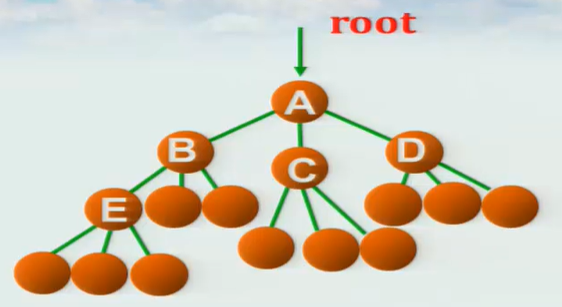
存储结构定义：

#define m 3
#define Maxsize 20
typedef char datatype; //结点值类型 
typedef struct node{  //结点结构体 
    datatype data;
    struct node* child[m]; 
}node;
typedef node* tree;

 

 功能函数：

tree createtree(){
    int i;
    char ch;
    tree t;
    if((ch=getchar())=='#')
        t=NULL;
    else{
        t=(tree)malloc(sizeof(node));
        t->data=ch;
        for(i=0;i<m;i++)
            t->child[i]=createtree();
    }
    return t;
} 

 

 四、树的遍历

1.前序遍历

先访问跟结点，然后依次访问根节点的每个子结点。

例1：👇前序遍历结果：ABEHIJCDFJK

 

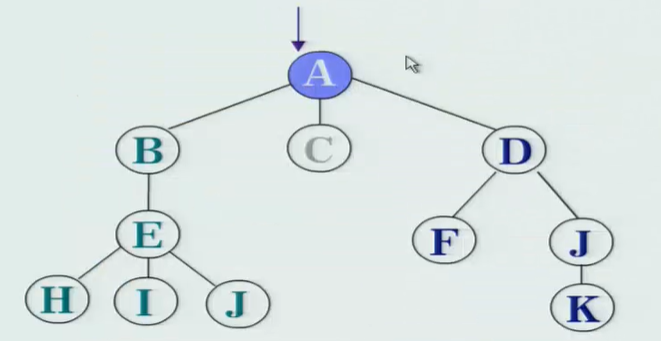
例2：👇前序遍历的结果是：ABCEFHIGD

 

 

2.中序遍历

因为树的度不确定，无法找出中序遍历的中间点，所以该方法只在二叉树中涉及。

 

3.后续遍历

先访问子树，再访问根节点

例1：👇后续遍历结果：HIJEBCFKJDA

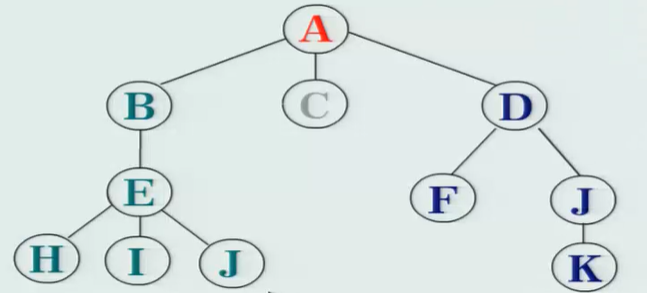
例2：下后续遍历的结果：BEHIFGCDA

 

4.层次遍历

按照树的层次，从根节点开始，一层一层的遍历

 例1：👇层次遍历的结果：ABCDEFGHI

 

 

(○｀ 3′○) 感谢观看，希望对你有帮助！