编译原理----文法和语言

字母表：符号的非空有限集。  例如∑={0，1，2}

 

符号：字母表中的元素。  例如：1

 

符号串：由字母表中的符号组成的任何有穷序列。  例如：01，012012，......

 

空符号串：ε

 

问：符号就是字符对吗？

答：不对。符号还可以是字符串，如C语言字母表中的符号{if，else，for......}

 

符号串的前后缀：从符号串S的尾部（头部）删去若干个（包括0个）符号之后所剩下的部分称为S的前（后）缀。

例如：011的前缀：ε，0，01，011

　　　011的后缀：011，11，1，ε

 

符号串集合：若集合A中的一切元素都是某字母表上的符号串，则称A为该字母表上的符号串集合。  例如：∑={a，b，c}   A={aa，ab，ac}

 

符号串的连接运算：符号串X和Y的连接是把Y的符号写在X的符号之后得到的符号串XY。

例如：X=01，Y=10，则XY=0110。

对于任意符号串S有：εS=Sε=S

 

符号串的幂运算：符号串自身连接n次得到的符号串Sⁿ=SS...SS。

例如：S=01， 则S⁰=ε，S¹=01，S²=0101，......

 

符号串集合的乘积：设A，B为符号串集合，则A和B的乘机定义为：AB={xy|x∈A，y∈B}

例如：A={a，b}，B={c，d}  ，则AB={ac，ad，bc，bd}

 

符号串集合的幂运算：例如A={0，1} 则A⁰={ε}，A¹={0，1}，A²={00，01，10，11}

 

符号串集合的闭包运算：

A⁺=A¹∪A²∪A³∪A⁴∪........       称为A的正闭包

A^*=A⁰∪A⁺          称为A的闭包

 例如：A={x，y} ，则A⁺={x，y，xx，xy，yx，yy，......} ，A*={ε，x，y，xx，xy，yx，yy，......} 

 

语言：是由句子组成的集合，是有一组符号所构成的集合

 

文法：是对语言结构的定义和描述（或称“语法”）

 

文法的形式定义：G[S]=（V_N，V_T，P，S）

　　　　　　　　　　V_N：非终结符号集

　　　　　　　　　　V_T：终结符号集

　　　　　　　　　　P：规则的集合

　　　　　　　　　　S：开始符号

 

直接推导：用产生式的右部替换产生式的左部

直接规约：用产生式的左部替换产生式的右部

 

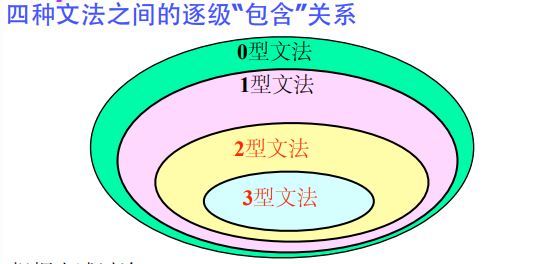
文法和语言的分类：0型，1型，2型，3型

0型文法：产生式左边始终包含至少一个非终结符号。（对0型文法做出某些限制可以的得到1，2，3型文法）。

1型文法：（上下文有关），aAb-->aBb只有在这样的a，b上下文中才能把A改写为B。

2型文法：（上下文无关），产生式左边一个非终结符号，右边为符号串（可以为空）。

3型文法：（正则文法），产生式左边一个非终结符号，右边只能为一个终结符号或者一个终结符号加一个非终结符号。A->Ba左线型，A->aB右线型。

 

 

文法的二义性：如果一个文法存在某个句子对应两棵不同的语法树，则说明这个文法是二义的。

 

句型分析：是指识别输入的符号是否为某一文法的句型（或句子）的过程。

 

最左(右)推导：指对于一个推导序列中的每一直接推导，被替换的总是当前符号串中的最左(右)非终结符号。最右推导也 称为规范推导。