洛谷 P1228 【地毯填补问题】
事实上感觉四个的形状分别是这样:
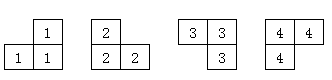
spj报错:
1:c 越界
2:x,y 越界
3:mp[x][y] 已被占用
4:mp[x][y] 从未被使用
题解:
初看这个问题,似乎无从下手,于是我们可以先考虑最简单的情况,既n = 2时
0 0 0 1 这时,无论公主在哪个格子,我们都可以用一块毯子填满
继续考虑n = 4的情况
我们已经知道了解决2 * 2的格子中有一个障碍的情况如何解决,因此我们可以尝试构造这种情况
首先,显然可以将4 4的盘面划分成4个2 2的小盘面,其中一块已经存在一个障碍了
而我们只需在正中间的2 * 2方格中放入一块地毯,就可以使所有小盘面都有一个障碍
于是,n = 4的情况就解决了
我们可以将n = 4时的解法可以推广到一般情况,既当n = 2 k时,我们均可以将问题划分为4个n = 2 k – 1的子问题,然后分治解决即可。
下面附上代码(算法:分治):
#include<cstdio>
typedef long long ll;
ll x,y,len; int k;
ll fun(int k)
{
ll sum=1;
for(int i=1;i<=k;++i) sum*=2;
return sum;
}
void solve(ll x,ll y,ll a,ll b,ll l)
{
if(l==1) return;
if(x-a<=l/2-1 && y-b<=l/2-1)
{
printf("%lld %lld 1\n",a+l/2,b+l/2);
solve(x,y,a,b,l/2);
solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
}
else if(x-a<=l/2-1 && y-b>l/2-1)
{
printf("%lld %lld 2\n",a+l/2,b+l/2-1);
solve(a+l/2-1,b+l/2-1,a,b,l/2);
solve(x,y,a,b+l/2,l/2);
solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
}
else if(x-a>l/2-1 && y-b<=l/2-1)
{
printf("%lld %lld 3\n",a+l/2-1,b+l/2);
solve(a+l/2-1,b+l/2-1,a,b,l/2);
solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
solve(x,y,a+l/2,b,l/2);
solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
}
else
{
printf("%lld %lld 4\n",a+l/2-1,b+l/2-1);
solve(a+l/2-1,b+l/2-1,a,b,l/2);
solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
solve(x,y,a+l/2,b+l/2,l/2);
}
}
int main()
{
scanf("%d %lld %lld",&k,&x,&y);
len=fun(k);
solve(x,y,1,1,len);
return 0;
}
如果大家满意就关注我吧!


