欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld。
希望与志同道合的朋友一起交流,我刚刚设立了了一个技术交流QQ群:433250724,欢迎对算法、技术、应用感兴趣的同学加入。
前面两篇回归(一)(二)复习了线性回归,以及L1与L2正则——lasso和ridge regression。特别描述了lasso的稀疏性是如何产生的。在本篇中介绍一下和lasso可以产生差不多效果的两种feature selection的方法,forward stagewise selection和最小角回归least angle regression(LARS)。尤其是LARS,网上很多资料写的不太清楚,我尽量写的清楚一点。本文主要是参考[1]的前面几章,大家可以直接看原文写的更清楚。
关于特征选择feature selection
在很多实际应用中,我们往往需要处理大量高维数据,其中存在很多噪音或者不相关的属性;而且维度越高计算量也越高。大多数工程师都会想到做一下特征选择,即挑选一部分有价值的属性维度用于计算,以期望在提高准确性的同时降低计算复杂度。那么如何进行特征选择呢?
一般来说可以分为有监督和无监督两大类,无监督的方法就是普适性的了,一般是希望从数据的分布、或者局部结构来找到区分性最好的属性,但是就是因为是无监督的,肯定不会对你所需要的任务有特别的倾向,选出来的不一定是最合适的特征。而有监督的选择肯定会基于训练样本的标记,使得选出来的特征会适合特定的任务,但是很难用到其他问题中。特征选择这个topic说实话被水了很多年,真正有价值的不见得多——很多以前觉得计算能力不足的问题选择随着CPU/GPU的性能提升,不再是瓶颈,那么很多降维的需求就没有了。现在还要做特征选择,一方面是希望找到真正有用的特征,另一方面是希望“稀疏”,事实证明稀疏性在提高模型的准确性以及降低overfitting方面都很有作用。
如果要看无监督的feature selection可以看一下浙大蔡登教授的Unsupervised Feature Selection for Multi-cluster Data [2],方法简单实用;在本文中,我们主要讨论两种有监督的选择方法,并且是基于greedy思想的。这两个方法和LASSO非常相关,上一篇中我也提过,LASSO本身也可以用来做特征选择。
问题描述
在本文中,用下图中的数据为例子来说明:
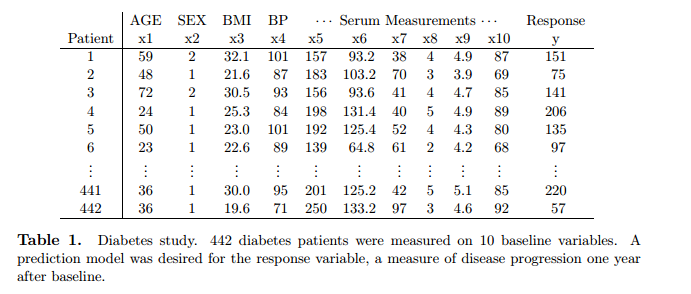
表 1
用X=(x1,x2,...,xn)T∈Rn×m表示数据矩阵,其中xi∈Rm表示一个m维度长的数据样本;y=(y1,y2,...,yn)T∈Rn表示数据的label,这里只考虑每个样本一类的情况。在表1的例子中,n=442,m=10。另外,假设数据是经过一些预处理的:样本中心化并且是列单位长度的,y是中心化的(减去均值),即
∑i=1nyi=0,∑i=1nxij=0,∑i=1nx2ij=1,j=1,2,…,m.
我们希望找到一个回归系数β^∈Rm,使得μ^=Xβ^。Lasso的优化目标是这样的:
minβ^=12∥y−μ^∥2,s.t.∑j=1m|βj^|≤t
其中参数t≥0。很明,当t不断增大的时候,对β^约束力就越来越小,当大到线性回归的β^的l1-norm的时候就没有约束力了。见图1左边,表示t不断增大的过程中,所有十个βj^的变化过程。很容易发现,在t比较小的时候,回归系数是稀疏的。比如在t=1000时,只有3、9、4、7维度是非零的。
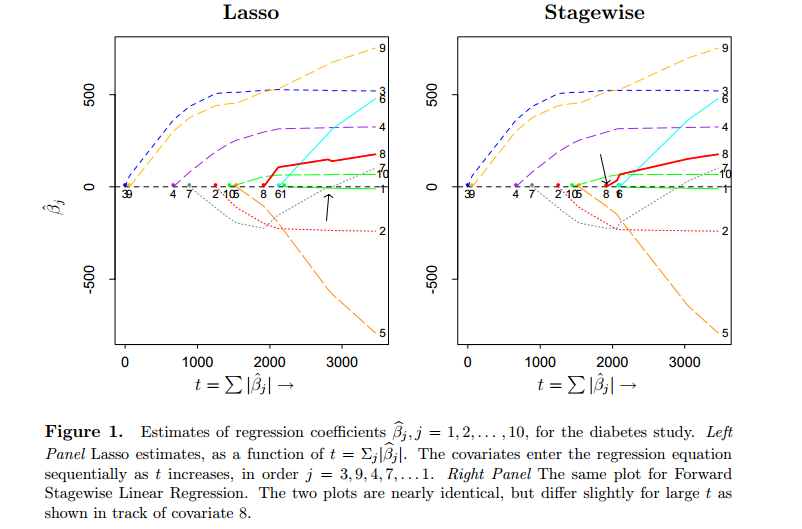
图1
forward stagewise selection
forward stagewise selection方法,下面简称为stagewise,是一个迭代算法。选择过程从μ^=0开始,并且不断向前走很小的step来完成回归模型(回归系数)。具体的过程如下:
令当前的回归预测是μ^,定义c(μ^)为当前的相关系数(current correlations):
c=c(μ^)=X′(y−μ^)
也就是说,
c^j是正相关于维度
xj∈Rn和当前残差的相关度。所以,下一步就是往相关系数最大的维度方向走一小步:
j^=argmax|c^j|andμ^→μ^+ϵ⋅sign(c^j^)⋅xj^
其中
ϵ是一个很小的常数——很小是很有必要的,如果很大的话就容易错过一些中间状态——比如,如果
ϵ=|c^j^|这么大的话stagewise方法就退化到了经典的“Forward Selection ”方法,是完全贪心选择的一次一个特征维度。但是在stagewise中,每次只会走很小一步,所以有可能在一个方向上走多步。图1的右图是stagewise的所有
βj^变化过程,大概有六千步很小的迭代,使得变化看起来很光滑。可以看到,Lasso和stagewise的结果看起来“几乎”是一样的,在比较小的
t的时候都会产生类似的稀疏的结果。
stagwise方法非常简单,易于实现,但是主要的问题是需要有大量的迭代步骤,因此计算量会比较大。事实上,不论是Lasso还是Stagewise方法都是Least angle regression(LARS)的变种。LARS的选择不需要经历那么多小的迭代,可以每次都在需要的方向上一步走到最远,因此计算速度很快,下面来具体描述一下LARS。
最小角回归Least angle regression,LARS
先用一个两维的例子来描述LARS的思路,后面再描述下任意维度下的统一算法。
LARS算法也是要得到形式为μ^=Xβ^的预测值,对于m维度的数据,最多只要m步就可以把所有的维度都选上,因此在迭代次数上是非常小的。下面图2说明了LARS在2维数据下的选择过程,X=(x1,x2)。
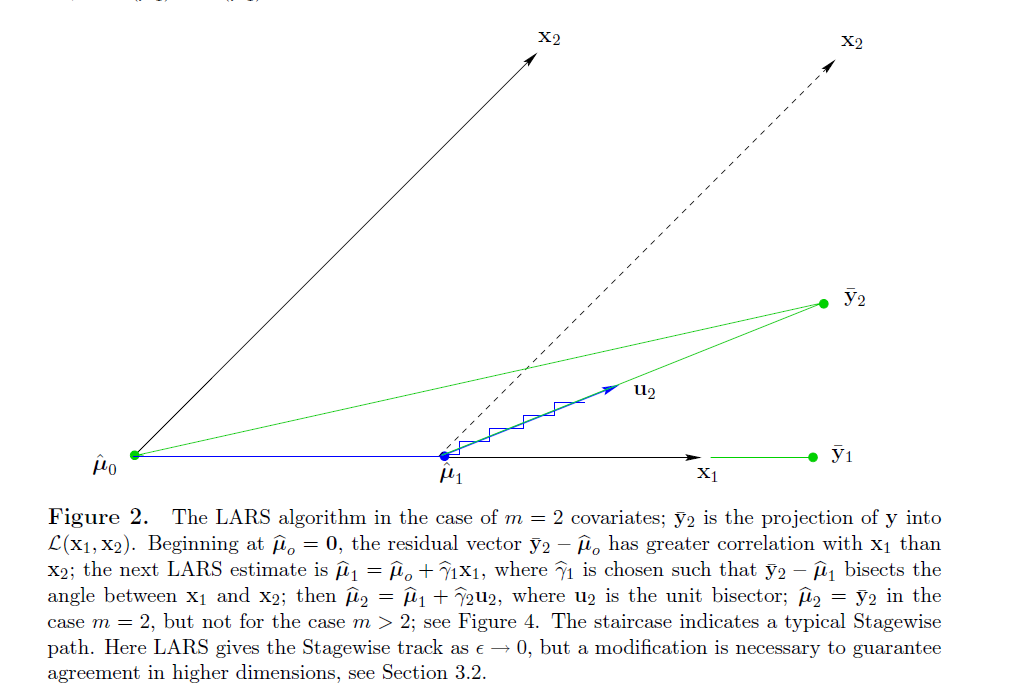
图2
对于前面一节提到的相关系数,我们可以把y等价替换成其在由x1,x2所张成的空间中的投影y¯2,即
c=c(μ^)=X′(y−μ^)=X′(y¯2−μ^)
算法也是从
μ^0=0开始的,从图2可以看出,
y¯2−μ^0显然更靠近
x1,也就是说,
c1(μ^0)>c2(μ^0),于是LARS会选
x1走一步,使得
μ^1=μ^0+γ^1x1
(在这里,如果是stagewise就选很小的
γ^1;而如果是Forward Selection,会选择一个足够大的
γ^1使得
μ^1=y¯1,即
y在
x1方向上的投影。)LARS会选择上面两个情况的一个中间结果——刚好使得
y¯2−μ^1可以平分
x1和
x2之间的夹角,因此,
c1(μ^1)=c2(μ^1)。 图2中可以看到上面的选择结果,
y¯2−μ^1是坐落在单位向量
u2的方向上的。下一步LARS的更新方向是:
μ^2=μ^1+γ^2u2
在
m=2的情况下,
γ^2是需要选择合适的大小使得
μ^2=y¯2,得到线性回归的结果。如果
m>2的情况下,LARS会继续探索更多的方向。图2中阶梯线表示stagewise的一个迭代过程,最后也攀爬到
y¯2。因此,其实LARS和stagewise的区别就在于,我们是可以计算出在一个方向上需要走多远的。
下面我们来讨论一下多维情况,和前面m=2一样,LARS的每一步都是沿着某一个角平分线的方向上走的。假设X的列向量x1,x2,…,xm都是线性无关的。记A是{1,2,…,m}的一个子集,定义矩阵
XA=(⋯sjxj⋯)j∈A
其中符号
sj=±1。定义
GA=XTAXA,以及
AA=(1TAG−1A1A)−1/2。其中
1A表示全1向量,长度和
A中的元素个数一样。对于
XA的角平分线方向上的单位向量
uA可以表示为:
uA=XAwA,wA=AAG−1A1A
使得和每一个
xj都有相同的角度(小于90度),并且
XTAuA=AA1A,and∥uA∥2=1
上面的可以当做结论,可以跳过证明部分。
证明:
1、首先uA肯定可以表示成XA的线性组合形式uA=XAwA,这里向量wA还是未知的;
2、uA平分X_{\mathbf{A}}XA,也就是说
XTAuA=XTAXAwA=z⋅1A
其中
z是一个常数,则
wA=z(XTAXA)−11A;并且
∥uA∥2=1,所以
z21TA(XTAXA)−1XTAXA(XTAXA)−11A=1z=(1TA(XTAXA)−11A)−1/2
得证。
好,接下来可以给出LARS的统一过程了。
假设当前步骤下LARS的预测结果是μ^A,所以要求当前的相关系数:
c^=c(μ^A)=X′(y−μ^A)
集合
A是其中拥有最大(绝对值)相关系数的维度的标号集合。
C^=maxj{|c^j|}andA={j:|c^j|=C^}
根据之前分析的,我们可以计算出
XA=(⋯sjxj⋯)j∈A
AA=(1TAG−1A1A)−1/2,GA=XTAXA
uA=XAwA,wA=AAG−1A1A
同时定义:
a=X′uA
那么下一步LARS更新μ^A会采用:
μ^A+=μ^A+γ^uA
γ^=min+j∈Ac⎧⎩⎨C^−c^jAA−aj,C^+c^jAA+aj⎫⎭⎬.
其中min+表示取正数部分的最小值,并且会把这个最小γ^值对应的j^这个维度加入到选出来的特征维度集合A了。新的active set是A+=A∪{j^}。
证:
如果当前步骤下LARS的预测结果是μ^A,那么下步之后的预测(会加进一个维度j)就是
μ(γ)=μ^A+γuA
其中γ>0,那么这个时候X所有维度xj的相关系数就是
cj(γ)=xTj(y−μ(γ))=xTj(y−(μ^A+γuA))=c^j−γaj
如果j∈A(在当前已选的集合里),那么,
|cj(γ)|=C^−γ(XTAXAwA)j=C^−γAA
从前面的AA=(1TAG−1A1A)−1/2可以知道AA>0,也就是说所有之前挑选出来的维度的相关系数(最大的相关系数)都等值地进行衰减(因为往uA走了一步,所以减去一个小的正值γAA)。
这个时候,对于那些j∈Ac的维度,如果要把一个j也加到A里面,就要cj(γ)=c^j−γaj=C^−γAA,此时可以算出一个γ;当然也可能相关系数是负的,所以c^j−γaj=−(C^−γAA),此时也可以算出一个γ;所以实际上我们是取上面两个γ中的较小值,同时,对所有j∈Ac都要做check取出一个最小的γ^,
γ^=min+j∈Ac⎧⎩⎨C^−c^jAA−aj,C^+c^jAA+aj⎫⎭⎬.
这个最小γ^值对应的j^这个维度就可以被加入到选出来的特征维度集合A了。新的active set是A+=A∪{j^}。最大(绝对值)相关系数是C^−γ^AA。
得证。
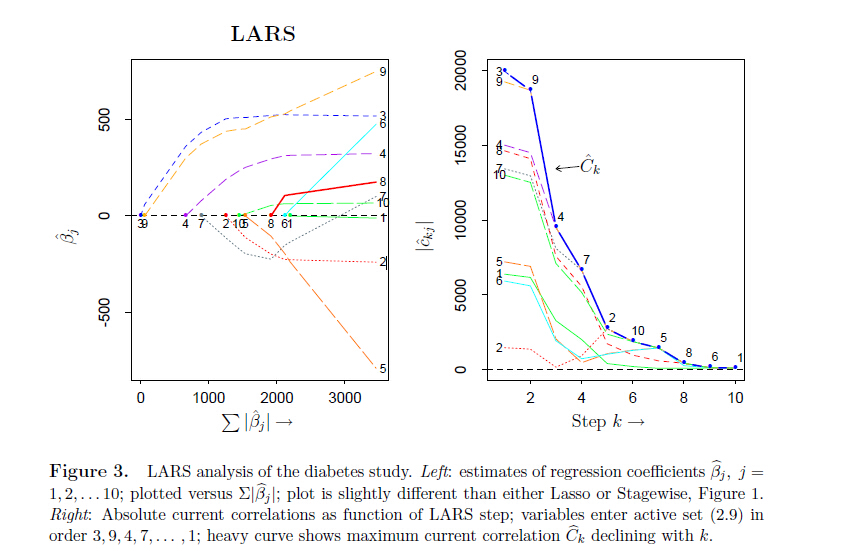
图3
图3是LARS的特征变化图,和图1类比,发现三种方法的结果看起来几乎都差不多,事实上他们也确实产生类似的稀疏系数。(关于LARS如何改造成LASSO可以参考[1]和[3]的先关章节,稍作修改即可,本文等后面有时间再补。)图3右图画的是相关系数的绝对值数值大小随着迭代选择的步数k的变化,
|c^kj|=|x′j(y−μ^k−1)|
可以看到不同的维度一旦被选择后就会一起衰减了,前面已经讨论过。
在LARS过程中,我们每一步都可以直接得到预测值μ^A,不过如果我们希望得到μ^A=Xβ^A中稀疏的β^A(只有选出来的维度非零)。应该这么做呢?假设我们当前的β^A是已知了的,根据前面的讨论,下一步是
μ^A+=μ^A+γ^uA=Xβ^A+γ^XAwA=X(β^A+γ^δA)
其中δA是吧wA从|A|长扩展成m维度长——把j∈A位置的元素用wA中相应元素,其余位置补零。这样就得到了下一步的稀疏系数应该是β^A+γ^δA。
这一篇就写到这里,描述了两种和lasso相关性强的特征选择方法,都可以产生稀疏的结果。尤其是LARS,每次选择都可以最优策略地加进一个维度,使得最多m步就可以结束算法。本系列到目前为止的(一)(二)(三)都和线性回归相关,线性回归三部曲到这里就暂告段落;接下来准备写一下决策树、逻辑回归等基础。加油加油!
参考资料
[1] Bradley Efron,Least Angle Regression
[2] dengcai, Unsupervised Feature Selection for Multi-cluster Data,KDD2010
[3] The Elements of Statistical Learning

