【枚举】 最大子矩阵(I)

题注：最大子矩形问题的解决办法最初由中国国家集训队王知昆前辈整理并发表为论文，在此说明并感谢。

Definition

　　给你一个大矩形，里面有一些障碍点，求一个面积最大的矩形，满足该矩形在大矩形内部且该矩形内部没有特殊点。矩形边界可以含有障碍点。这一类问题被称为最大子矩形问题。

Solution

　　首先引用一些由王知昆前辈定义的概念：

　　　　有效子矩形：合法的子矩形。

　　　　极大子矩形：对于一个有效子矩形，如果不存在完全包含它的有效子矩形，则该矩形是一个极大子矩形。

　　　　最大子矩形：所求的面积最大的有效子矩形

定理一：

　　　　一个最大子矩形一定是一个极大子矩形。

证明：

　　　　　　假设最大子矩形A不是极大子矩形，那么一定存在一个有效子矩形完全包含A，那么该矩形比A大且合法，则A不是最大子矩形。与假设矛盾。故一个最大子矩形一定是一个极大子矩形。

证毕。

定理二：

　　　　最大子矩形的四周一定不能再向外拓展。具体地，最大子矩形的四周边界上要么存在障碍点，要么是大矩形的边界。

证明：

　　　　　　假设最大子矩形的四周能向外扩展，那么它就不是一个极大子矩形。与【定理一】矛盾。

证毕。

　　这样，我们直接考虑枚举所有的障碍点作为矩形边界，判断它是不是一个合法的矩形，如果是，则更新答案。

　　记障碍点的个数是k，那么这么做的复杂度是\(O(k^5)\)。GG

　　考虑我们枚举每个点作为矩形的左边界，不断向右枚举它的右边界，能否顺手处理它的上下边界？

　　显然，对于左边界相同的矩形，右边界更靠右的矩形的上边界不高于靠左的矩形，下边界不低于更靠左的矩形。

　　那么我们可以每次枚举一个障碍点作为左边界，向右枚举右边界，每次更新上边界和下边界。

　　具体的方法为：每扫描到一个新的点，按照当前维护的上下边界计算面积并更新，更新后，如果当前点的竖直坐标高于左边界上的点，更新上边界，如果当前点的竖直坐标低于左边界上的点，更新右边界。

考虑特殊情况：如果两个点的竖直坐标相等，那么如何更新。

　　在这种情况下如果继续更新上边界或下边界，那么左边界就会同时作为上边界或下边界。如图：
　　
　　

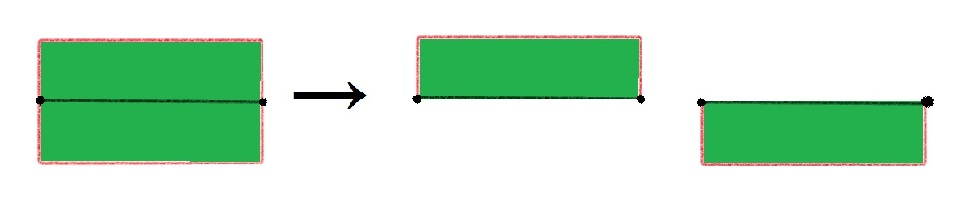
　　将枚举分为两种情况：左侧障碍点只作为左边界；左侧障碍点同时作为左边界和上或下边界。

　　对于第一种情况，遇到竖直坐标相等直接break。因为后面不会产生左侧障碍只作为左边界的矩形。

　　对于第二种情况，每次扫描维护矩形向上拓展和向下拓展的最大值，不断更新。讲左侧障碍点作为上或下边界，不断更新面积。对于特殊情况，因为它在边界上对答案没有影响，直接忽略即可。

考虑是否将矩形枚举完全：我们只考虑了左边界是障碍点的情况，对于左边界是大矩形左侧的情况没有枚举到。

　　对于这种矩形，分成两种情况：只有左侧是大矩形边界，右侧是障碍点；左右两侧都是大矩形边界。

　　我们将大矩形四个角上四个点都加入到障碍点中，按照上面的算法，对于第一种情况可以通过被从右向左扫描一遍解决掉。

　　下面讨论第二种情况：

定理三：

　　　　　　一个左右边界都在大矩形的左右边界上的子矩形是极大子矩形充要条件是上下边界是按照竖直坐标排序后相邻的两个障碍点。

证明：

　　　　　　　　充分性：假设上下边界的障碍点不是相邻的，那么显然存在k在两个点之间，从而在矩形内部，矩形不合法。

　　　　　　　　必要性：假设子矩形的上下边界不是障碍点，那么它不是一个极大子矩形。

证毕。

　　那么我们将障碍点按照竖直坐标排序，则他们之间矩形的面积是相邻两个障碍点的高度差和大矩形横向长度的乘积。每次更新答案即可。

Example

【P1578】奶牛浴场

description

由于John建造了牛场围栏，激起了奶牛的愤怒，奶牛的产奶量急剧减少。为了讨好奶牛，John决定在牛场中建造一个大型浴场。但是John的奶牛有一个奇怪的习惯，每头奶牛都必须在牛场中的一个固定的位置产奶，而奶牛显然不能在浴场中产奶，于是，John希望所建造的浴场不覆盖这些产奶点。这回，他又要求助于Clevow了。你还能帮助Clevow吗？

John的牛场和规划的浴场都是矩形。浴场要完全位于牛场之内，并且浴场的轮廓要与牛场的轮廓平行或者重合。浴场不能覆盖任何产奶点，但是产奶点可以位于浴场的轮廓上。

Clevow当然希望浴场的面积尽可能大了，所以你的任务就是帮她计算浴场的最大面积。

Input

输入文件的第一行包含两个整数L和W，分别表示牛场的长和宽。文件的第二行包含一个整数n，表示产奶点的数量。以下n行每行包含两个整数x和y，表示一个产奶点的坐标。所有产奶点都位于牛场内，即：\(0~\leq~x~\leq~L\)，0_\leqy_\leqW。

Output

输出文件仅一行，包含一个整数S，表示浴场的最大面积。

Sample Input

10 10
4
1 1
9 1
1 9
9 9

Sample Output

80

Hint

\(0~\leq~n~\leq~5000\)

\(1~\leq~L,W~\leq~30000\)

Solution

板子题要啥solution？

Code

#include<cstdio>
#include<algorithm>
#define rg register
#define ci const int
#define cl const long long int

typedef long long int ll;

namespace IO {
	char buf[100];
}

template <typename T>
inline void qr(T &x) {
	char ch=getchar(),lst=' ';
	while(ch>'9'||ch<'0') lst=ch,ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	if(lst=='-') x=-x;
}

template <typename T>
inline void write(T x,const char aft,const bool pt) {
	if(x<0) {putchar('-');x=-x;}
	int top=0;
	do {
		IO::buf[++top]=x%10+'0';
		x/=10;
	}while(x);
	while(top) putchar(IO::buf[top--]);
	if(pt) putchar(aft);
}

template <typename T>
inline T mmax(const T _a,const T _b) {if(_b<_a) return _a;return _b;}
template <typename T>
inline T mmin(const T _a,const T _b) {if(_a>_b) return _b;return _a;}
template <typename T>
inline T mabs(const T _a) {if(_a<0) return -_a;return _a;}

template <typename T>
inline void mswap(T &_a,T &_b) {
	T _temp=_a;_a=_b;_b=_temp;
}

const int maxn = 35010;

struct M {
	int x,y;
	inline M (int _a=0,int _b=0) {x=_a,y=_b;}
	inline bool operator<(const M &_others) const {
		return this->x<_others.x;
	}
};
M MU[maxn];

inline bool cmp(const M &_a,const M &_b) {
	return _a.y<_b.y;
}

int l,w,n;
int ans;

int main() {
	qr(l);qr(w);qr(n);
	for(rg int i=1;i<=n;++i) {
		qr(MU[i].x);qr(MU[i].y);
	}
	MU[++n]=M(0,0);MU[++n]=M(l,0);MU[++n]=M(0,w);MU[++n]=M(l,w);
	MU[0] = M(-1,-1);
	std::sort(MU+1,MU+1+n,cmp);
	for(rg int i=1;i<n;++i) {
		rg int upceil = 0,downfloor = l;
		rg int j=i+1;
		while(MU[j].y==MU[i].y) ++j;
		while(j<=n) {
			ans=mmax(ans,(downfloor-upceil)*(MU[j].y-MU[i].y));
			if(MU[j].x<MU[i].x) upceil=mmax(upceil,MU[j].x);
			else if(MU[j].x>MU[i].x) downfloor=mmin(downfloor,MU[j].x);
			else break;
			++j;
		}
		j=i+1;upceil=0;downfloor=l;
		while(MU[j].y==MU[i].y) ++j;
		while(j<=n) {
			ans=mmax(ans,(MU[j].y-MU[i].y)*mmax(MU[i].x-upceil,downfloor-MU[i].x));
			if(MU[j].x<MU[i].x) upceil=mmax(upceil,MU[j].x);
			else if(MU[j].x>MU[i].x) downfloor=mmin(downfloor,MU[j].x);
			++j;
		}
	}
	for(rg int i=n;i>1;--i) {
		rg int upceil = 0,downfloor = l;
		rg int j=i-1;
		while(MU[j].y==MU[i].y) --j;
		while(j) {
			ans=mmax(ans,(downfloor-upceil)*(MU[j].y-MU[i].y));
			if(MU[j].x<MU[i].x) upceil=mmax(upceil,MU[j].x);
			else if(MU[j].x>MU[i].x) downfloor=mmin(downfloor,MU[j].x);
			else break;
			--j;
		}
		j=i-1;upceil=0;downfloor=l;
		while(MU[j].y==MU[i].y) --j;
		while(j) {
			ans=mmax(ans,(MU[i].y-MU[j].y)*mmax(MU[i].x-upceil,downfloor-MU[i].x));
			if(MU[j].x<MU[i].x) upceil=mmax(upceil,MU[j].x);
			else if(MU[j].x>MU[i].x) downfloor=mmin(downfloor,MU[j].x);
			--j;
		}
	}
	rg int _temp=0;
	std::sort(MU+1,MU+1+n);
	for(rg int i=1;i<n;++i) {
		_temp=mmax(_temp,MU[i+1].x-MU[i].x);
	}
	ans=mmax(ans,_temp*w);
	write(ans,'\n',true);
}

Summary

这样的算法是有一定局限性的。当大矩形边界范围很大并且障碍点数较小时，使用本算法可以避免对坐标进行离散化降低代码难度并通过剪枝提升程序效率。但事实上，记大矩阵是 \(m~\times~n\)的矩阵，那么障碍点的个数上限会达到 \(m~\times~n\)，\(m\)与\(n\)较大时讲难以接受。

存在一种只与矩形大小有关的算法。将在后面的blog介绍。

再次感谢王知昆前辈