【数据结构】带权并查集

百度百科

没有带权并查集的百科

注：感谢@DDYYZZ julao与我的讨论

Definition&Solution

　　对于普通并查集，我们维护f[a]为a的父节点。但是在一些对父子关系有严格要求的问题中，我们并不能简单的通过f[a]=find(f[a])将a的父亲直接指向a的祖先。似乎解决办法只有不进行路径压缩。但是需要注意的是，不进行路径压缩的复杂度为O(mn)，其中m为操作个数，n为最大节点个数。对于一般的题目都无法承受。换一种思路，我们使用deepth[i]点i距离i的根节点的距离。这样，我们就可以一边进行路径压缩一边保留节点间的关系了。

　　要深入理解带权并查集的操作流程，首先需要深入了解普通路径压缩并查集是怎么工作的。例如，有如下两个集合：

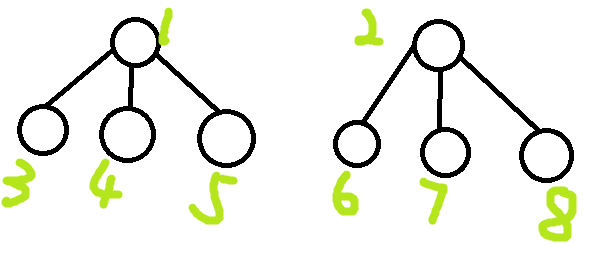
现在需要合并两个集合。合并后结果如图：

 

现在假如我们要合并3和另一节点，我们调用find(3)。其中find函数写法如下

int find(int x) {
    return f[x]==x?x:f[x]=find(f[x]);
}

这句话翻译后，是将自己节点的父亲接到父节点的父亲上。合并后效果如图：

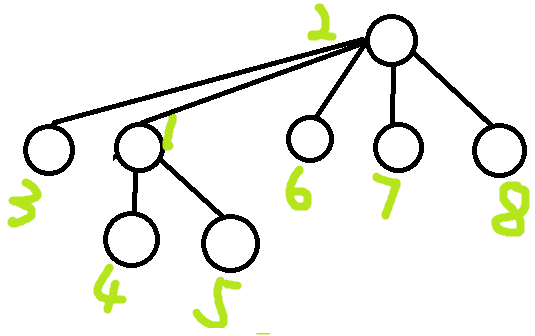
可以发现，真正对树形造成更改从而保证复杂度的，是find操作，而不是合并操作。在一次合并的时候，被合并节点的子树上的节点的信息并不是合法的（即不满足路压并查集的要求）。但是每次调用find函数时，通过父节点的信息更新子节点的信息，从而保证从被调用的节点到根节点的链上是合法的。由于根节点显然是合法的，整个过程的合法性可以通过数学归纳证明。

现在考虑最基本的带权并查集：对于两个已知链，将一条链的顶端合并到另一条链的尾部。询问链上两点间的距离。

我们不妨用deepth[i]代表i到i的父节点在链上的实际距离。考虑合并两条新链的时候，我们维护一个参数size[i]代表i所在链的长度。不妨设以i为头的链连接到以j为头的链的尾部，那么显然有deepth[i]=size[j],f[i]=j。

显然j原有的链上节点的信息是合法的，但是原来i链上的信息全部是不合法的。如何解决呢？考虑在find函数中通过父节点更新子节点的合法信息。当f[i]合法时，我们通过路径压缩将i点连接到f[i]的父节点上，归纳法易证i点会被连接到根节点上。（在这个问题中，根节点就是该链顶端的节点标号）那么deepth[i]应该记录i到根节点的实际距离。但这时deepth[i]存储的是i到f[i]的实际距离。但是注意到在归纳时i的父节点的信息已经是合法的了，那么deepth[f[i]]就应该等于f[i]到根节点的距离。显然，deepth[i]=deepth[i]+deepth[f[i]]。在等号右边，deepth[i]存储的是i到f[i]的实际距离。更新后，deepth[i]被更新为到根节点（顶端）的距离了。这样就可以保证我们用到的每个点，他们的信息都是合法的。需要注意的是，凡是经过路压的点，最终都会形成根-子孙的两层结构。由于我们进行了路径压缩，deepth[i]的合法值就是i到根节点的的距离。那么每次询问的答案就是abs（deepth[i]-deepth[j]）+1了。

下面是find函数的写法：

#define ci const int
int find(ci x) {
    if(frog[x]==x) return x;
    int k=frog[x];frog[x]=find(frog[x]);
    deepth[x]+=deepth[k];
    return frog[x];
}

以及合并函数

inline void cont(ci x,ci y) {
    int fa=find(x),fb=find(y);
    if(fa==fb) return;
    frog[fa]=fb;deepth[fa]=sz[fb];sz[fb]+=sz[fa];sz[fa]=sz[fb];
}

 

Example

lgP1196 [NOI2002]银河英雄传说

Description

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成 $30000$ 列，每列依次编号为 $1,2,\dots ,30000$ 。之后，他把自己的战舰也依次编号为 $1,2,\dots ,30000$ ，让第 $i$号战舰处于第 $i$ 列 $(i=1,2,\dots ,30000)$ ，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为 $M^{i,j}$ ，含义为第i号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令： $C^{i,j}$ 。该指令意思是，询问电脑，杨威利的第 $i$ 号战舰与第 $j$ 号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

Input

第一行有一个整数 $T(1\le T\le 500,000)$ ，表示总共有 $T$ 条指令。

以下有 $T$ 行，每行有一条指令。指令有两种格式：

1. $M^{i,j}$ ： $i$ 和 $j$ 是两个整数 $(1\le i,j\le 30000)$ ，表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第 $i$ 号战舰与第 $j$ 号战舰不在同一列。

2. $C^{i,j}$ ： $i$ 和 $j$ 是两个整数 $(1\le i,j\le 30000)$ ，表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

Output

依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第 $i$ 号战舰与第 $j$ 号战舰之间布置的战舰数目。如果第 $i$ 号战舰与第 $j$ 号战舰当前不在同一列上，则输出 $-1$ 。

Sample Input

4
M 2 3
C 1 2
M 2 4
C 4 2

Sample Output

-1
1

Hint

$(1\le T\le 500,000)$  

$(1\le i,j\le 30000)$

Solution

模板题

Code

#include<cstdio>
#define maxn 30010
#define ci const int

inline void qr(int &x) {
    char ch=getchar(),lst=NULL;
    while(ch>'9'||ch<'0') lst=ch,ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    if(lst=='-') x=-x;
}

template <typename T>
inline T mmax(const T &a,const T &b) {if(a>b) return a;return b;}
template <typename T>
inline T mmin(const T &a,const T &b) {if(a<b) return a;return b;}
template <typename T>
inline T mabs(const T &a) {if(a>=0) return a;return -a;}

template <typename T>
inline void mswap(T &a,T &b) {T temp=a;a=b;b=temp;}

int t,a,b;
int frog[maxn],deepth[maxn],sz[maxn];

int find(ci);
int ask(ci,ci);
void cont(ci,ci);

int main() {
    qr(t);
    for(int i=1;i<=30000;++i) frog[i]=i,sz[i]=1;
    while(t--) {
        char ch=getchar();while(ch!='M'&&ch!='C') ch=getchar();
        a=b=0;qr(a);qr(b);
        if(ch=='M') cont(a,b);else printf("%d\n",ask(a,b));
    }
    return 0;
}

int find(ci x) {
    if(frog[x]==x) return x;
    int k=frog[x];frog[x]=find(frog[x]);
    deepth[x]+=deepth[k];
    return frog[x];
}

inline void cont(ci x,ci y) {
    int fa=find(x),fb=find(y);
    if(fa==fb) return;
    frog[fa]=fb;deepth[fa]=sz[fb];sz[fb]+=sz[fa];sz[fa]=sz[fb];
}

inline int ask(ci x,ci y) {
    int fa=find(x),fb=find(y);
    if(fa!=fb) return -1;
    return mabs(deepth[x]-deepth[y])-1;
}

300