【神奇性质】【P5523】D [yLOI2019] 珍珠

D [yLOI2019] 珍珠

Description

给定一个 deque，要求支持 push_back 和 push_front 操作，并且查询前缀与非和以及后缀与非和。

deque中只会有 $0$ 或 $1$，一共有 $n$ 次操作，其中有 $m$ 次操作给定，剩下的操作随机。

Limitations

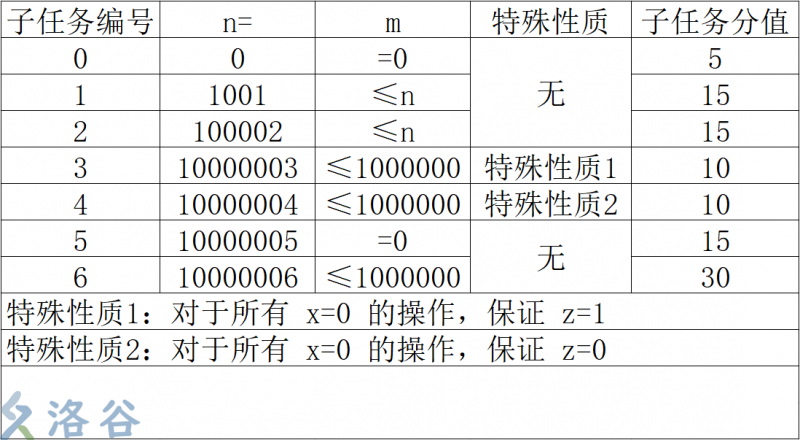
Solution

这是一道通过输入格式来防AK的题目

下面的做法只考虑前缀与非和，因为后缀的做法与前缀完全相同。

子任务 $0$：

没有操作，输出四个 $0$ 即可。期望得分 $5~pts$

子任务 $1$：

暴力模拟，每次从前面插入的时候后面的元素暴力移位，暴力查询与非和即可。时间复杂度 $O(n^2)$，期望得分 $15~pts$

子任务 $2$：

考虑用线段树来维护每个区间的与非和，但是这样产生了一个问题，两个区间的与非和是无法合并的，因为与非运算没有交换律和结合律。

但是我们注意到事实上对于某个区间，序列的首部到区间左端点之前所有元素的与非和只可能是 $0$ 或 $1$，因此线段树每个节点维护两个信息：当该区间之前所有元素的与非和是 $0$ 时与非上该区间的值，以及当该区间之前元素与非和是 $1$ 时与非上该区间的值，然后即可 $O(1)$ 转移。

时间复杂度 $O(n \log n)$，期望得分 $15 ~pts$

子任务 $3$：

插入的元素全部是 $1$。

考虑一堆连续 $1$ 的前缀与非和序列，一定形如 $101010101\dots$

证明上，考虑第一个位置一定是 $1$，然后 $1~\text{nand}~1~=~0$ ，$0~\text{nand}~1~=~1$，因此序列中 $0$ 和 $1$ 一定是循环出现的。

因此一个询问的答案一定是 $y~\&~1$。时间复杂度 $O(n)$，期望得分 $10~pts$

子任务 $4$：

插入的元素全部是 $0$。

考虑一堆 $0$ 的前缀与非和序列，一定形如 $011111111111 \dots$

用与子任务 $3$ 类似的办法即可解决。时间复杂度 $O(n)$，期望得分 $10~pts$

子任务 $5$：

考虑一个显而易见的事实，$0$ 与非任何数都得 $1$。

因此考虑一次查询如果与非和的最后一项是 $0$，则直接返回 $1$ 即可。

同时对于最后一项是 $1$ 的操作，只需要看这一项向前一共有连续的几个 $1$，由于前面那一项是 $0$，所以一段 $011111$ 的序列的与非和一定是 $1010101010\dots$，而与 $0$ 前面的项完全无关。

当然需要特判查询的 $0$ 是序列第一个元素，以及查询的 $1$ 前面没有 $0$ 的情况。

那么问题就变成了对于每个位置维护它前面第一个 $0$ 的位置。

由于 $m = 0$ ，序列中的元素是完全随机的，因此连续 $0/1$ 段的长度期望都是常数级的，因此暴力找即可，期望时间复杂度 $O(n)$，期望得分 $15~pts$

子任务 $6$：

考虑在序列不随机时怎么对每个数维护它前面第一个 $0$ 的位置。

事实上，在每插入一个 $0$ 时，都暴力修改这个 $0$ 的有元素的一侧的连续 $1$ 的信息即可。

例如，在序列左侧插入一个 $0$，则暴力修改 $0$ 右侧连续 $1$ 的左侧最近的 $0$ 的位置为该位置即可。在序列右侧插入同理。

考虑时间复杂度：每个为 $1$ 的元素都只会在左侧最近和右侧最近的 $0$ 插入的时候被修改信息，因此每个元素都只会被修改 $O(1)$ 次信息，即每次均摊修改 $O(1)$ 个信息，总的修改次数为 $O(n)$，因此总时间复杂度 $O(n)$，期望得分 $30~pts$。

appreciation

感谢@Burnside 神仙帮助进行题解的校对工作