【线段树】【P5522】[yLOI2019] 棠梨煎雪

C [yLOI2019] 棠梨煎雪

Background

岁岁花藻檐下共将棠梨煎雪

自总角至你我某日辗转天边

天淡天青 宿雨沾襟

一年一会信笺却只见寥寥数言

——银临《棠梨煎雪》

Description

给定 $m$ 个长度为 $n$ 的可能含有 ？ 的 01 串，其中 ? 既能代表 0 也能代表 1， $q$ 次操作，每次给定一个区间，求有多少 01 串满足区间内的所有字符串都可以解释成该 01 串，或者单点修改某个字符串。

Limitations

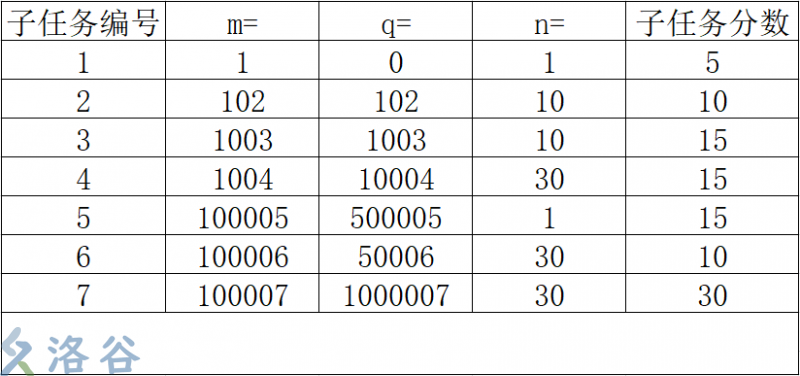
Solution

子任务 $1$：

输出 $0$ 即可得分，期望得分 $5~pts$。

子任务 $2$：

考虑 $n$ 只有 $10$，因此可以 $O(2^n)$ 去枚举所有可能的串，然后对于每个询问 $O(m)$ 的逐个判定是否合法。时间复杂度 $O(qm2^n)$，期望得分 $10~pts$。

子任务 $3$：

考虑对于一段所有字符串的第 $x$ 个字符，一共有四种可能：确定为 $0$；确定为 $1$；都可以；都不可以。如果 $0/1$ 都不可以，则答案为 $0$，因为不会有任何一个字符串匹配该区间。如果确定为某个数，则这一位只有一种可能；否则这一位有两种可能。根据乘法原理，如果有 $a$ 个位置有两种可能，则本次询问的答案为 $2^a$。

因此对于每个询问，$O(nm)$ 地去遍历区间内所有字符即可。时间复杂度 $O(nmq)$，期望得分 $15~pts$。

子任务 $4$：

考虑 $n$ 只有 $30$，可以状压到 int 中。具体的，维护两个 int，第一个 int 维护对应位是否确定是 $0$ 或 $1$，第二个 int 维护如果确定是 0 或 1 了那么具体是 0 还是 1。

例如，对于单个字符串，它所有的为 ? 的位置，在第一个 int 中对应位置是 0，所有为 0 或 1 的位置，在第在个 int 中对应的位置是 1，在第二个 int 中对应的位置是自身的值。

考虑 $a_1,~a_2$ 是询问的左端点到某个字符串之前所维护的两个 int，$b_1,~b_2$ 是该字符串的两个 int，现在合并这两个信息。

如果某一位置即不可以是 $1$，也不可以是 $0$，那么该字符串不为 ? 的位置在 $b_2$ 中对应的值应该至少有一个和 $a_2$ 中对应位置的值且 $a_1$ 的该位置为 $1$，位运算可以表现为 $(a1~\&~b_1)~\&~(a_2~\oplus~b_2) ~\neq 0$，则该询问的答案为 $0$。

否则这两段信息可以合并：将他们已经确定字符的位置合并起来，然后将确定位置对应的值合并起来即可。于是 $a_1$ 对 $b_1$ 取或， $a_2$ 对 $b_2$ 取或即可。

最终该询问 $0/1$ 都可以的位置的个数即为 $a_1$ 中 $1$ 的个数。

时间复杂度 $O(mq)$，期望得分 $15~pts$

子任务 $5$：

由于 $n$ 只有 $1$，问题变成了求某个区间内的字符是不是全是 0，全是 1，全是 ? 或 0 和 1 都有。可以考虑用线段树非常轻松的维护这样的信息。

时间复杂度 $O(q \log m)$，期望得分 $15~pts$

子任务 $6$：

世界上没有什么事情是开一棵线段树不能解决的，如果有，那就开 $30$ 棵。

时间复杂度 $O(nq \log m)$，期望得分 $10~pts$

子任务 $7$：

考虑结合子任务 $4$ 和子任务 $5$ 的做法，发现两个区间的状压信息也可以用子任务 $4$ 的方法合并。因此用线段树维护这两个 int 的状压信息即可。

时间复杂度 $O(q \log m)$，期望得分 $30~pts$