排序

排序low B三人组

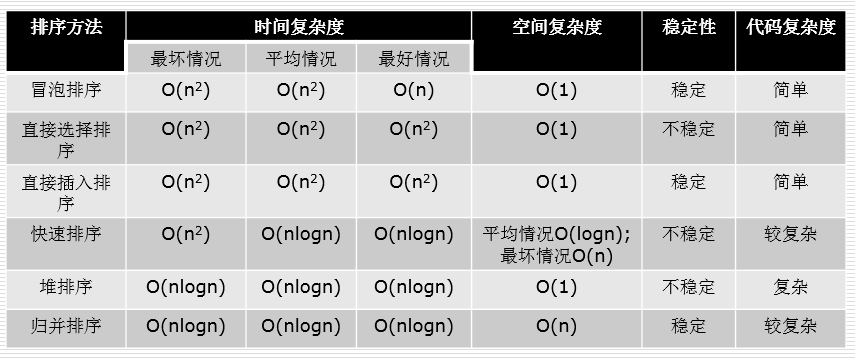
- 冒泡排序　　　　　　　　比较相邻的元素。如果第一个比第二个大，就交换他们两个。依次进行排序。

#冒泡排序
    - 列表每相邻的数,如果前边的比后边的大,那么交换这两个数
    - 算法复杂度 n^2


import random

def bubble_sort(li):
    for i in range(len(li) - 1):                # i 趟
        for j in range(len(li) - i -1):         # j 指针
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j]
    return li

li = list(range(10))
random.shuffle(li)
obj = bubble_sort(li)
print(obj)

- 选择排序　　　　　　　  一趟遍历记录最小的数，放到第一个位置。再一趟遍历剩余

# 选择排序
    - 一趟遍历记录最小的数,放到第一个位置;再一趟遍历记录剩余列表中最小的数,继续放置...
    - 时间复杂度 O(n^2)


def select_sort(li):
    for i in range(len(li) - 1):    #i 趟
        min_loc = i
        # 找i+1位置到最后面位置内最小的数
        for j in range(i+1,len(li)):
            if li[j] < li[min_loc]:
                min_loc = j
        # 和无序区第一个数作交换
        li[min_loc],li[i] = li[i],li[min_loc]
    return li

obj = select_sort([1,8,6,2,5,3])
print(obj)

- 插入排序 　　　　　　　 摸牌插入，将牌从无序区放到手中有序区，最开始手中有序区只有一张，后面抽牌放入手中有序区。

#插入排序
    - 列表被分为有序区和无序区 最初有序区只有一个元素
    - 每次从无序区选择一个元素 插入到有序区的位置 直到无序区变空


#方式一:

def insert_sort(li):
    for i in range(1,len(li)):  # i 代表每次摸到牌的下标
        tmp = li[i]
        j = i-1   # j代表手里最后一张牌的下标
        while True:
            if j<0 or tmp>=li[j]:
                break
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp
    return li

obj = insert_sort([1,8,6,2,5,3])
print(obj)


#方式二:

def insert_sort(li):
    for i in range(1,len(li)):  # i 代表每次摸到牌的下标
        tmp = li[i]
        j = i-1   # j代表手里最后一张牌的下标
        while j>=0 and tmp<li[j]:
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp
    return li

obj = insert_sort([1,8,6,2,5,3])
print(obj)

排序NB二人组

- 堆排序

def shift(data,low,high):        # shift函数复杂度：O(logn)
    """
    调整函数
    data: 列表
    low：待调整的子树的根位置
    high：待调整的子树的最后一个节点的位置
    """
    i = low                    # i指向空位置
    j = 2*i + 1        
    tmp = data[low]
    while j<=high:            #领导已经撸到底了
        if j != high data[j] < data[j+1]
            j+=1            #j指向数值大的孩子
        if tmp<data[j]:        #如果小领导比撸下来的大领导能力值大
            data[i] = data[j]
            i = j
            j = 2*i+1
        else:                #撸下来的领导比候选的领导能力值大
            data[i] = tmp
            break
    else:
        data[i] = tmp
        
        
@cal_time
def heap_sort(data):        # heap_sort函数复杂度：O(nlogn)
    n = len(data)
    # 建堆 
    for i in range(n//2-1,-1,-1):        
        shift(data,i,n-1)
    # 挨个出数
    for high in range(n-1,-1,-1):
        data[0],data[high] = data[high],data[0]
        shift(data,0,high-1)

堆排序

- 归并排序

# 一次归并
def merge(li,low,mid,high):
    i = lowe
    j = mid+1
    ltmp = []
    while i <= mid and j <= high:
        if li[i] <= li[j]:
            ltmp.append(li[i])
            i +=1
        else:
            ltmp.append(li[j])
            j +=1
    while i<=mid:
        ltmp.append(li[i])
        i += 1
    while j<=high:
        ltmp.append(li[j])
        j += 1
        
    li[low:high+1] = ltmp
    

def mergesort(li,low,high):
    if low<high:
        mid = (low+high)//2
        mergesort(li,low,mid)
        mergesort(li,mid+1,high)
        merge(li,low,mid,high)

快速排序

def partition(data,left,right):

    tmp = data[left]
    while left < right:
        # right 左移动
        while left < right and data[right] >= tmp:   #如果low和high没有相遇且后面的数一直大于第一个数 就循环
            right -=1
        data[left] = data[right]
        # left 右移动
        while left < right and data[left] <= tmp:   #如果low和high没有相遇且后面的数一直大于第一个数 就循环
            left +=1
        data[right] = data[left]
    data[left] = tmp
    return left


def quick_sork(data,left,right):

    if left <right:
        mid = partition(data,left,right)
        quick_sork(data,left,mid-1)
        quick_sork(data,mid+1,right)
    return data


alist = [33,22,11,55,33,666,55,44,33,22,980]

obj = quick_sork(alist,0,len(alist)-1)
print(obj)

备注：

　　说道排序其实python内置了（sorted）排序，一行就可以搞定

print(sorted([1,4,2,7,3,8,2]))

 def qsort(seq):

    if seq==[]:
        return []
    else:
        pivot=seq[0]
        lesser=qsort([x for x in seq[1:] if x<pivot])
        greater=qsort([x for x in seq[1:] if x>=pivot])
        return lesser+[pivot]+greater
 
if __name__=='__main__':
    seq=[5,6,78,9,0,-1,2,3,-65,12]
    print(qsort(seq))

　　

 

递归实例：汉诺塔问题

import time

def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2 - t1))
        return result
    return wrapper
t = 0
def hanoi(n, A, B, C):
    global t
    if n > 0:
        hanoi(n - 1, A, C, B)
        t += 1
        hanoi(n - 1, B, A, C)

@cal_time
def _hanoi(n):
    return hanoi(n, 'A', 'B', 'C')
_hanoi(25)
print(t)

　　

　　

 

二分法

　　例1、已知列表li=[5,7,7,8,8,10] 和 target = 8，求列表二个不同索引的value值相加为target，并且算法复杂度为O(log n).即：li[a]+li[b]=target,返回索引值

def bin_search(data_set,val):
    low = 0
    high = len(data_set) - 1
    while low <= high:
        mid = (low+high)//2
        if data_set[mid] == val:
            a = mid
            b = mid
            while data_set[a] == val and a>0:
                a -= 1
            while data_set[b] == val and b<len(data_set):
                b += 1
            return (a+1,b-1)
        elif data_set[mid] > val:
            high = mid - 1
        else:
            low = mid + 1
    return None

　　例2、已知列表li=[2, 7, 11, 15]，target=9,  li[i]+li[j]=target，索引i不等于j. 求i，j

法一：
    def two_sum(li, target):
        l = len(li)
        for i in range(l):
            for j in range(i+1, l):
                if li[i] + li[j] == target:
                    return (i, j)
        return None

    print(two_sum([2, 7, 11, 15], 17))
    
    
法二： 二分查找
    
    def bin_search(data_set, value):
        low = 0
        high = len(data_set) - 1
        while low <= high:
            mid = (low + high) // 2
            if data_set[mid] == value:
                return mid
            elif data_set[mid] > value:
                high = mid - 1
            else:
                low = mid + 1

    def two_sum_2(li, target):
        li.sort()
        for i in range(len(li)):
            b = target - li[i]
            j = bin_search(li, b)
            if j != None and i != j:
                return i, j

    print(two_sum_2([2, 7, 11], 14))
    
    
法三：

    def two_sum_3(li, target):
        li.sort()
        i = 0
        j = len(li) - 1
        while i<j:
            sum = li[i]+li[j]
            if sum > target:
                j-=1
            elif sum < target:
                i+=1
            else: #sum==target
                return (i,j)
        return None