算法
算法是解决特定问题求解步骤的描述，再计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。
数据结构和算法关系
数据结构和算法就像梁山伯与祝英台，罗密欧与朱丽叶，少了一个主角，光讲另一个主角的心路旅程就没法看了。
本文的算法只是为了帮助理解好数据结构，不会详谈算法的细节。
算法的特性
五项基本：输入、输出、有穷性、确定性和可行性。
1.输入：算法具有零个或多个输入。
2.输出：算法至少有一个或多个输出。输出形式可以是打印或返回值
3.有穷性：指算法在执行有限的步骤后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成。
注：有穷的理解并非纯数学意义上的，而是实际应用当中合理的、可以接受的“有边界”。比如，写了一个算法，计算机需要算个20年，一定会结束，数学意义上是有穷，但算法的意义就不存在了。
4.确定性：算法的每一步骤都具有确定的含义，不会出现二义性。
5.可行性：算法的每一步都必须是可行的，也就是说，每一步都能够通过执行有限次数完成。
算法设计的要求
1.正确性
算法的正确性是指算法至少应该具有输入、输出、和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。
正确性的层次：
- 算法程序没有语法错误。
- 算法程序对于合法的输入数据能够产生满足要求的输出结果。
- 算法程序对于非法的输入数据能够得到满足规格说明的结果。
- 算法程序对于精心选择的，甚至***难的测试数据都有满足要求的输出结果。
2.可读性
算法设计的另一目的是为了便于阅读、理解和交流。
可读性高有助于人们理解算法，晦涩难懂的算法往往隐含错误，不易被发现，并且难于调试和修改。
3.健壮性
当输入数据不合法时，算法也能做出相关处理，而不是产生异常或莫名其妙的结果。
4.时间效率高和存储量低
时间效率指的是算法的执行时间，执行时间越短，算法效率越高。、
存储量需求指的是算法在执行过程中需要的最大存储空间，只要指算法程序运行时所占用的内存或者外部硬盘存储空间。
算法效率的度量方法
1.事后统计方法
这种方法主要时通过设计好的测试程序和数据，利用计算机计时器对不同算法编制的程序的运行时间进行比较，从而确定算法效率的高低。
缺点：因为缺陷比较明显，一般不用
- 必须依据算法事先编制好程序，这通常需要花费大量的时间和精力。如果编制出来本身就是糟糕的算法，那就竹篮打水一场空了。
- 时间的比较依赖计算机硬件和软件等环境因素，有时会掩盖算法本身的优劣。就算同一台机器，CPU使用率和内存占用情况不一样，也会造成细微的差异
- 算法的测试数据设计困难，并且程序的运行时间往往还与测试数据的规模有很大关系，效率高的算法在小的测试数据面前往往得不到体现。
2.事前分析估量方法
在计算机程序编制前，依据统计方法对算法进行估算。
程序编写影响因素：
- 算法采用的策略、方法。
- 编译产生的代码质量。
- 问题的输入规模。
- 机器执行指令的速度。
一个程序的运行时间，依赖于算法的好坏和问题的输入规模。
问题的输入规模：输入量的多少。
第一种算法，执行了1+（n+1) + n + 1 = 2n+3次
第二种算法，执行了 1+1+1 = 3次
例子延伸：
不难看出，这里计算1002次。
在分析程序的运行时间时，最重要的时把程序看成是独立于程序设计语言的算法或一系列步骤。
分析一个算法时间时，重要的是把基础操作的数量与输入规模关联起来，即基本操作的数量必须表示成输入规模的函数。如图：
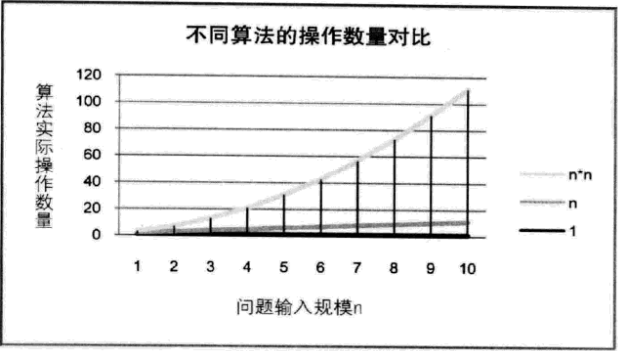
图中三种算法随着n值的越来越大，时间效率上的差异也就越来越大。
函数的渐近增长
输入规模n在没有限制的情况下，给定两个函数f(n)和g(n)，如果存在一个整数N，使得对于所有的n>N, f(n)总是比g(n)大，那么，我们说f(n)的增长渐近快于g(n)。
当n = 1时， 算法A效率比不上算法B（次数比算法B多1次）。当n>2时，算法A就开始优于算法B了，随着n的增加，算法A比算法B越来越好（执行的次数比B要少）。于是我们可以得出结论，算法A总体上要好于算法B。
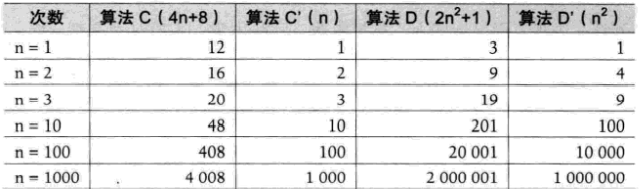
1.随着n的增大，后面的+3和+1已经影响不到最终算法变化了，如算法A‘和算法B’，所以，我们可以忽略这些加法常数。
2.与高次项相乘的常数并不重要，如下图：
3.最高次项的指数大的，函数随着n的增长，结果也会变得增长特别快，如下图：
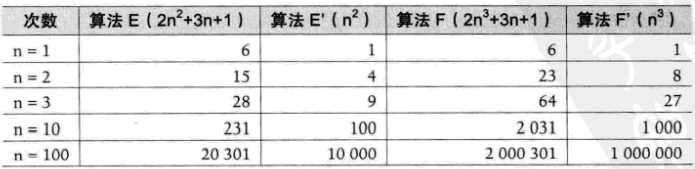
4.判断一个算法效率时，函数中的常数和其它次要项常常可以忽略，而更应该关注主项（最高阶项）的阶数。
如下图：算法G其实已经很趋近与算法I
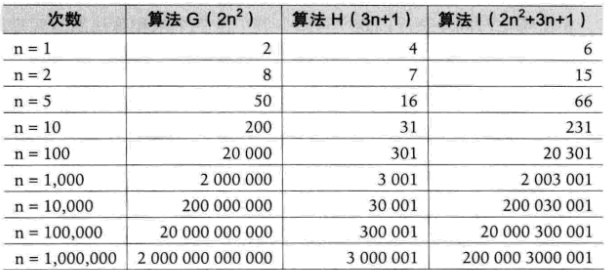
注：由上所述，判断一个算法好不好，只通过少量的数据是不能做出准确判断的。
结论：某个算法，随着n的增大，它会越来越优于另一个算法，或者越来越差与另一个算法。
算法时间复杂度
定义：在进行算法分析时，语句总的执行次数T(n)时关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，也就是算法的时间量度，记作：T(n) = O(f(n))。它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中f(n)时问题规模n的某个函数。
大写O()来体现算法时间复杂度的记法，我们称之为大O记法。
一般情况下，随着n的增大，T(n)增长最慢的算法为最优算法。
由此算法时间复杂度定义可知，我们的三个求和算法的时间复杂度分别为O(n), O(1), O(n2)。我们分别给它们取了非官方名称， O(1)叫常数阶、O(n)叫线性阶、O(n2)叫平方阶。
推导大O阶方法
- 1.用常数1取代运行时间中的所有加法常数
- 2.在修改后的运行次数函数中，只保留最高阶项。
- 3.如果最高阶项存在且不是1，则去除与这个项相乘的常数
得到的结果就是大O阶。
事实上，分析一个算法的时间复杂度，没有这么简单的。
常数阶
顺序结构的时间复杂度。时间复杂度O(1),如下图：
这个算法运行次数函数时f(n) = 3。根据大O结推导法，第一步把常数项改成1。它没有最高阶项，所以这个算法时间复杂度为O(1)。
f(n) = 12, 12和3的差异与n的多少无关，执行时间恒定算法，同样时O(1)
所以，我们称之为具有O(1)的时间复杂度，叫做常数阶。
线性阶
分析算法的复杂度，关键就是要分析循环结构的运行情况。如下：
int i; for (i = 0; i < n; i++) { /* 时间复杂度为O(1)的程序步骤序列 */ }
因为循环体中的代码须要执行n次，这种循环的时间复杂度为O(n)。
对数阶
由于每次count乘以2之后，距离n更近一分。也就是说，有多少个2相乘后大于n，则会退出循环。由2x=n得到 x=log2n。所以这个循环的时间复杂度为O(logn)。
平方阶
内循环如线性阶的分析，时间复杂度为O(n)。而对于外层的循环，不过时内部这个时间复杂度为O(n)的语句，再循环n次，所以这段代码的时间复杂度为O(n2)。如果外循环次数改为了m，时间复杂度就变为O(m * n)。
由此可以总结出，循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
由于当i=0时，内循环执行了n次， 当i=1时，执行了n-1次，。。。。当i=n-1时，执行了1次。
所以总执行次数为： n+(n-1)+.....+1 = n(n+1)/2 即 n2/2 + n/2
根据推导大O阶方法，第一条，没有加法常数不考虑，第二条，只保留最高阶项，因此保留n2/2，第三条，去除这个项的常数，也就是去除1/2， 最终这段代码的时间复杂度为O(n2)。
注：理解大O推导不算难，难的时对数列的一些相关运算，更多时考察数学知识和能力。
同理
它的执行次数f(n) = 1+n+n2+n(n+1)/2 = 3n2/2 + 3n/2+1,时间复杂度也是O(n2)。
常见的时间复杂度
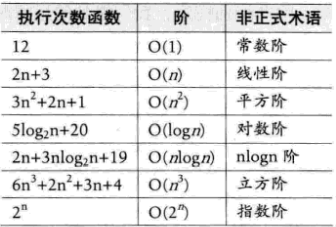
常用的时间复杂度所耗费的时间从小到大依次时：
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
指数阶以及阶乘阶除非是很小的n值，哪怕n只是100，都是噩梦般的运行时间，所以基本不用
最坏情况和平均情况
最坏情况运行时间是一种保证，那就是运行时间将不会再坏了。再应用中，这是一种最重要的需求，通常，除非特别指定，我们提到的运行时间都是最坏情况的运行时间。
如：我们查找一个由n个随机数字数组的某个数字，最好的情况是第一个数字，那么算法时间复杂度是O(1)，但也可能这个数字再最后一个位置上，那么时间复杂度就是O(n)，这是最坏的一种情况了。
平均运行时间是所有情况中最有意义的，因为它是期望的运行时间。
我们运行一段程序代码时，是希望看到平均运行时间的。可现实中平均运行时间很难通过分析得到，一般都是通过运行一定数量的实验数据后估算出来的。
对算法的分析，一种方法时计算所有情况的平均值，这种时间复杂度的计算方法成为平均时间复杂度。
另一种方法时计算最坏情况下的时间复杂度，这种方法称为最坏时间复杂度。一般没有特殊说明的情况下，都是指最坏时间复杂度。
算法空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作：S(n) = O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。
通常，我们使用“时间复杂度”来指运行时间的需求，使用“空间复杂度”指空间需求。当不用限定词地使用“复杂度”时，通常都是指时间复杂度。
