树形递归
Tree Recursion
递归:函数体中直接或间接调用函数自身,则称其是递归的。
树形递归:函数体中调用函数自身多次
示例1
斐波那契数列
def fib(n): """ 效率还比较糟糕,如计算fib(35) 0 1 1 2 3 5 8 13 21 >>> fib(0) 0 >>> fib(1) 1 >>> fib(8) 21 """ if n == 0 or n == 1: return n else: return fib(n-1) + fib(n-2)
示例2
计算一个正整数n在上限为n时的最大分割可能数
如下图表示计算组成6的所有正整数组合,且所有组合中的数要小于4
下图调用将返回9
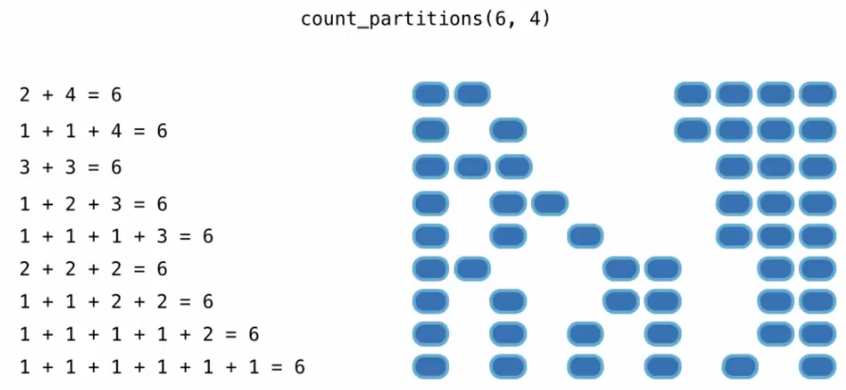
思路
递归的思想就是缩减问题规模,直至到一个不可再拆分的基底情况。不同于斐波那契数列,递归中需要控制的变量只有表示是第几个斐波那契数的n,因此只需要将n的基底情况0和1的返回值确定,之后就是递归调用了。
在当前问题中,有两个变量,一个是待拆分数n,另一个是组合可能最大数m,因此在考虑如何写递归函时,应当将两个变量的可能交叉组合,考虑所有的基底情况。
这时绘制图表可以帮助我们整理自己的思路,不至于混淆或遗漏。

设若n小于0,则不符合函数要求,返回0,即没有可能;
设若n为0,则不管m等于多少,都有一种可能,即自己本身什么都不加;
设若m等于0,则只要n不为0,都返回0,即没有可能要求的组合。
以上都是最基础的情况,剩下的一个就是要着重考虑的了,也就是要进行递归调用的情况。
假设调用count_partitions(6, 4),削减问题规模的话,可以知道它的值就是count_partitions(6, 3)加上一端固定为4时的所有可能。
这时,问题就变为如何用程序语言表述后者。如果只看向另一端,在当前例子中,就是可能组合的数不大于4时的2的所有组合,也就是count_partitions(6-4, 4)。
这样最后一种情况也就表示出来了。图示如下:

代码
def count_partitions(n, m): """ the number of partitions of a positive integer n, using parts up to size m, is the number of ways in which n can be expressed as the sum of positive integer parts up to m in an increasing order 对n而言上限为m-1的可拆分数 + 对n而言一侧为m的可拆分数(即对n-m而言上限为m的可拆分数) >>> count_partitions(6, 4) 9 >>> count_partitions(5, 3) 5 """ if n == 0: return 1 elif n < 0: return 0 elif m == 0: return 0 else: with_m = count_partitions(n-m, m) without_m = count_partitions(n, m-1) return with_m + without_m
示例3
在一个width * height的栅格长方形中,有一只毛虫蜷缩在左下角,另有一出口在右上角。如果它只能向上或向右移动,那么要达到出口,总共有多少种可能?
思路
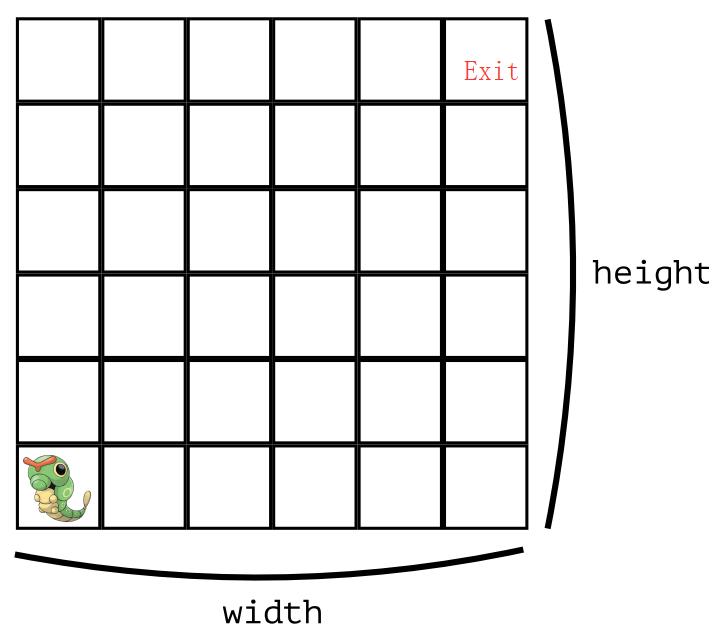
在这个问题中,到达出口的可能数不由毛虫决定,而是由长方形的宽和高决定。也就是这次的递归中要控制的两个变量,一个是height,另一个是width。
还是从最基础的情况开始思考:
设若宽和高都是1,那可能就只有一种,也就是待着不懂;
设若宽是1,那么高无论是多少,也都只有一种可能,就是沿着唯一的一条路向上走,别无他法;
设若高是1,那么宽无论是多少,也都只有一种可能,就是沿着唯一的一条路向右走,逃出生天;
有图示如下
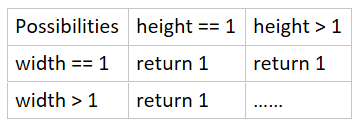
接下来考虑剩下的最后一种情况:宽和高都大于1时,毛虫可以怎么走?
那我们就将毛虫放在一个6 * 6(width * height)的长方形中去考虑。
已知毛虫只能向右走或向上走,不可反方向行动,那毛虫第一步开始就只有两种可能,每一种可能都可以依此为基础向下延申出其它可能。那么所有可能数就可表述为第一步向上走后所有可能数之和加上第一步向右走后的所有可能数之和。代入到当前例子中,毛虫第一步向右走后,就可视作其此时处在一个5 * 6的长方形中;毛虫第一步向上走后,就可视作其此时处在一个6 * 5的长方形中。如下图:
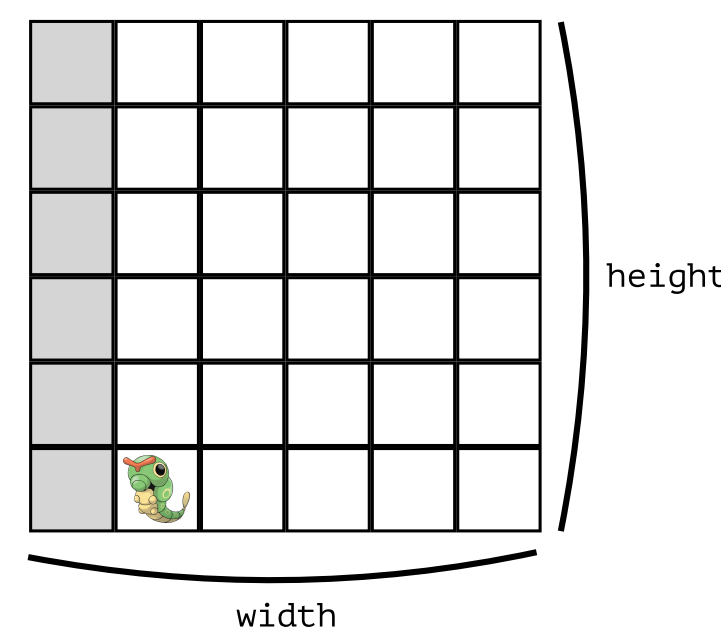
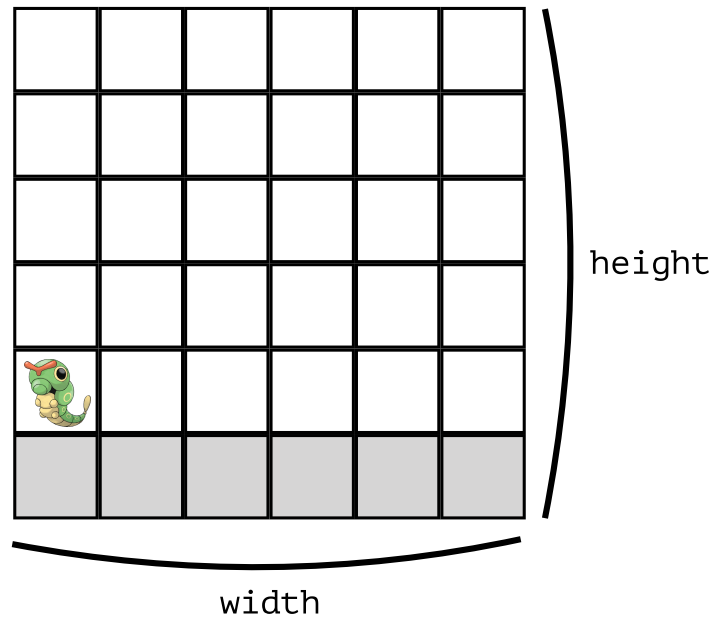
这就是分割当前问题的方法了,用程序也可以很容易地表示了。有图如下:

代码
def count_paths(width, height): """ In a rectangle grid of certain width and height, a caterpillar who can only move right or up is on the bottom left grid. In order to reach the exit at right top grid, How many different paths can the caterpillar take? >>> count_paths(1,1) 1 >>> count_paths(1,9) 1 >>> count_paths(10,1) 1 >>> count_paths(3,3) 6 """ if width == 1 and height == 1: return 1 elif width == 1 and height > 1: return 1 elif width > 1 and height == 1: return 1 else: return count_paths(width-1, height) + count_paths(width, height-1)
为了更清晰表达思路,也可简化如下:
def count_paths_simpler(width, height): """ >>> count_paths(1,1) 1 >>> count_paths(1,9) 1 >>> count_paths(10,1) 1 >>> count_paths(3,3) 6 """ if width == 1 and height == 1: return 1 else: caterprie_goes_up = count_paths(width-1, height) caterprie_goes_right = count_paths(width, height-1) return caterprie_goes_right + caterprie_goes_up
示例3
简化的背包问题
有一背包,和若干物品,各有其重,物品要放入背包中,且背包重物品的数量不可超过背包的最大承重。
另外物品也各有其价值,但这次为简化问题,暂不考虑各自价值,只求共有多少种装包方法。
思路
该问题仍是一个计算可能组合数的问题。物品可表示为一个元素为元组的列表,形如items = [(worth, weight),...]。
仍从最特殊的基本情况开始思考。因为基本情形中,不再有类似1 * 1长方形的基本单位,于是就从有无开始考虑,不再以1为基底。
设若没有物品,那不管背包能不能承重,都只有一种可能,就是什么都不放;
设若背包承重为0,物品也有的话,也就是有东西要放,背包却不能放重量大于0的物品,此时有几种可能呢?
这时,假设物品的重量可以为0,那么可能性就有很多,也就是取决于物品数量。这还可以算作是基底情况吗?
所谓的基底情况,必须足够简单,不会有不确定的可能。
换个思路,如果背包重量不以等于0为起点,而是以小于0为起点,那么无论有无物品,都只有0种可能了,因为就算什么也不放,也超过了最大承重0。
此时,将大于等于0归于一种情况。设若没有物品的话,那就只有一种情况,就是什么也不放。有图示如下:
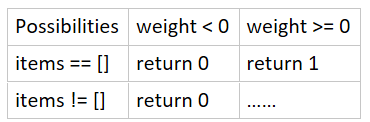
又留下了需要递归调用的最后一种情况。
再次只考虑最简单的问题。目光转向第一个物品,对其的处理只有两种可能,要么放入背包,要么不放入背包,其它可能组合也都以此为基础延申。
设若放入背包,那此时背包的最大承重就要减去物品的重量,剩下的问题就在当前重量下如何放入其它物品;
设若不放入背包,那背包的最大承重不变,剩下的问题就是在原最大承重下如何放入其它物品。
这也就是我们要进行递归调用的地方。有图如下:
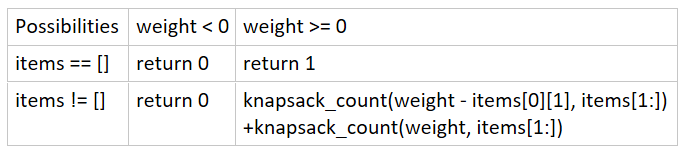
代码
def knapsack_count(weight, items): """ :param weight: maximum weight of the knapsack :param items: [(worth, weight), (worth, weight)] :return: how many ways we can fill the knapsack without going over the weight limit >>> knapsack_count(-1, [(10, 2)]) 0 >>> knapsack_count(3, []) 1 >>> knapsack_count(10, [(1, 4), (2, 5)]) 4 """ if weight < 0: return 0 if len(items) == 0: return 1 with_first_item = knapsack_count(weight - items[0][1], items[1:]) without_first_item = knapsack_count(weight, items[1:]) return with_first_item + without_first_item
示例4
人民币面额有100元、50元、20元、10元、5元、1元,共计6种。问任意特定数额共有多少种组合方式?
思路
该问题由SICP一书中树形递归一节的问题转换而来。原题是以美国的half-dollars, quarters, dimes, nickels, and pennies(50,25,10,5,1)为基础,
本土化后大概就变成了这个样子。但究其本质,思路无二。
该问题中有两个变量,一个是钱币总额,另一个是零钱种类(虽然100元对我而言不算零钱)。还从基底情况开始考虑。
假设总额为0,那不管有多少种零钱,都只有一种组合方式,就是什么都不放;
假设总额小于0,则都没有任何一种组合方式可以满足条件;
假设种类为0而且总额不等于0,那么也是没有任何一种组合方式可以达到要求。
可绘制图表如下:
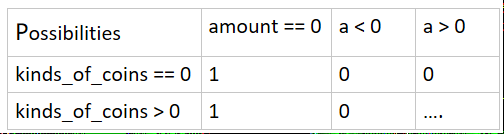
接下来考虑需要用到递归的地方。
不妨这样思考:任何对大于0的数额的组合方式,都相当于不使用第一种零钱的所有组合方式,加上去所有使用第一种零钱的组合方式。
代码
def count_change(amount, kinds_of_coins): """ >>> count_change(10, 2) 3 >>> count_change(100, 6) 344 """ if amount == 0: return 1 elif amount < 0 or kinds_of_coins == 0: return 0 else: # 所有不使用第一种零钱的组合方式 return (count_change(amount, kinds_of_coins - 1) # 所有使用第一种零钱的组合方式 + count_change(amount - first_denomination(kinds_of_coins), kinds_of_coins)) # 为了总额中扣除当前种类中第一种零钱的面额,要返回当前种类中第一种货币的面值 def first_denomination(kinds_of_coins): if kinds_of_coins == 6: return 100 elif kinds_of_coins == 5: return 50 elif kinds_of_coins == 4: return 20 elif kinds_of_coins == 3: return 10 elif kinds_of_coins == 2: return 5 elif kinds_of_coins == 1: return 1
下面也顺带贴一下原书中的racket语言实现方式(即美国钱币的例子):
(define (cc amount kinds-of-coins)
(cond [(= amount 0) 1]
[(or (< amount 0) (= kinds-of-coins 0)) 0]
[else (+ (cc amount (- kinds-of-coins 1)) (cc (- amount (first-denomination kinds-of-coins)) kinds-of-coins))]))
(define (first-denomination kinds-of-coins)
(cond ((= kinds-of-coins 1) 1)
((= kinds-of-coins 2) 5)
((= kinds-of-coins 3) 10)
((= kinds-of-coins 4) 25)
((= kinds-of-coins 5) 50)))
参考:
https://sequoia-tree.github.io/#Textbook
http://composingprograms.com/pages/17-recursive-functions.html
http://sarabander.github.io/sicp/html/1_002e2.xhtml#g_t1_002e2_002e1



