稀疏自动编码器 （Sparse Autoencoder）
摘要: 一个新的系列，来自于斯坦福德深度学习在线课程：http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial。本文梳理了该教程第一部分的内容，主要包括人工神经网络入门、反向传递算法、梯度检验与高级优化 和 自编码算法与稀疏性等要点。最后以课程作业作为总结和练习。
前言
斯坦福深度学习在线课程是 Andrew Ng 编制的，该教程以深度学习中的重要概念为线索，基本勾勒出了深度学习的框架。为了简明扼要，该教程几乎省略了数学推导和证明过程。我写这个系列不追求概念的讲解，因为教程已经解释的很清楚了，我的目标是把教程所省略的一些关键的数学推导给出来。因为数学原理是深入理解算法模型所绕不过去的，其次，几篇博客也是我的课程笔记，留作以后查阅使用。
综上，如果您已经阅读了对应的教程并理解了主要概念，这一系列能帮您查漏补缺深化理解，否则您会觉得文章的逻辑不连贯。
人工神经网络
人工神经网络的“学习”原理很简单：
每层都有若干个节点，每个节点就好比一个神经元（neuron），它与上一层的每个节点都保持着连接，且它的输入是上一层每个节点输出的线性组合。每个节点的输出是其输入的函数，把这个函数叫激活函数（activation function）。人工神经网络通过“学习”不断优化那些线性组合的参数，它就越有能力完成人类希望它完成的目标。
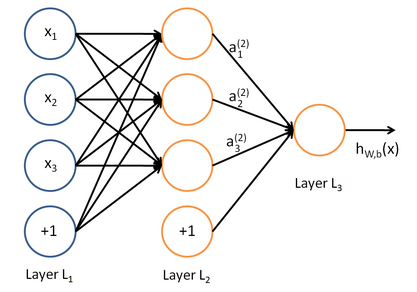
除了输入层（第1层）以外，第 l +1 层第 i 个节点的输入为：
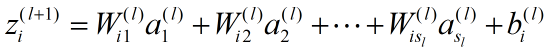
其中
是第 l 层的节点数。
第 l +1 层第 i 个节点的输出为：
当 l =1 时：
函数 f 就是激活函数。激活函数最常用的有两种：
sigmoid 函数
双曲正切函数
它们的函数曲线类似，都在（-∞，+∞）上单调递增：
sigmoid 函数值域为（0, 1）；而双曲正切函数的值域为（-1，1）。
对人工神经网络进行训练，就是为了得到最优的线性组合参数：
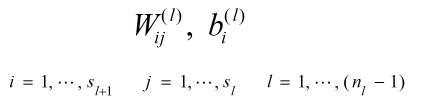
其中
是网络的总层数。
给定 m 个训练数据：
要用这些数据训练人工神经网络，使它能够对新的输入数据做正确的分类或拟合，首先要保证它在已有的数据上有足够高的正确率。
使用代价函数（Cost Function）来衡量人工神经网络在已有数据上所犯错误的大小：
注意，代价方程有多种形式，只要能反映预测误差即可。
对于单条数据 ，其代价方程为：
可见总代价方程是每条数据代价方程的算术平均。
在优化时，代价方程还会加上一个规则化项，其目的是减小权重的幅度，防止过度拟合：
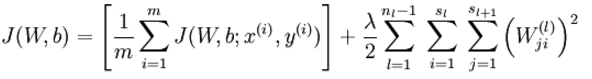
反向传播算法
反向传播算法从输出层开始，反向计算每个节点的残差，并用这些残差计算代价方程对每一个参数的偏导数。
反向传播算法的数学推导过程我在 这篇 文章里已经详细给出，这里在给出一个简洁版本。
对于一个样例 ：
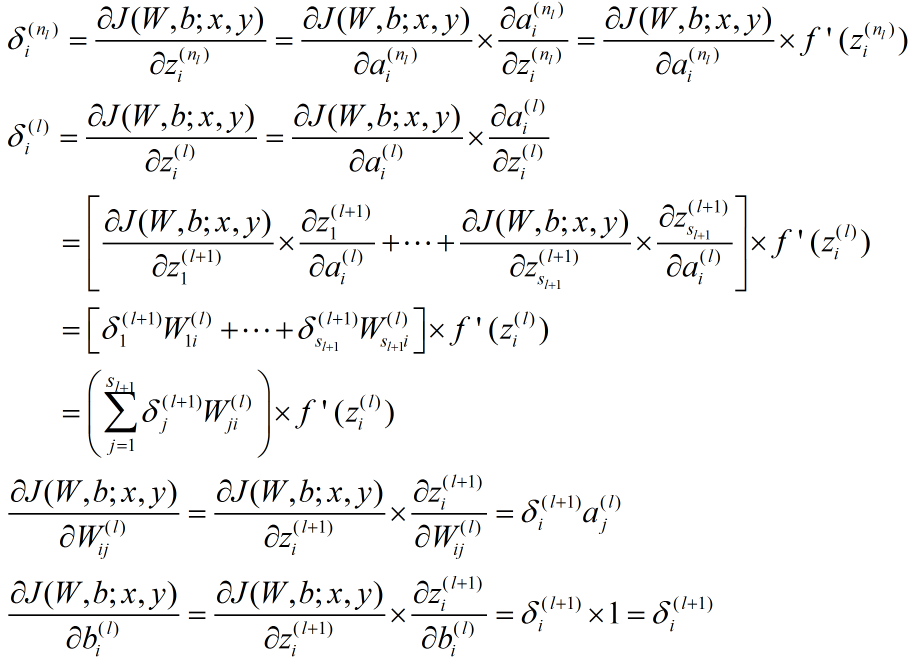
将公式向量化：
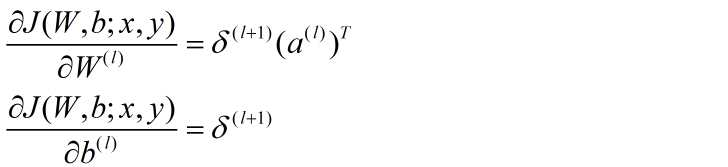
对于整个样本集：
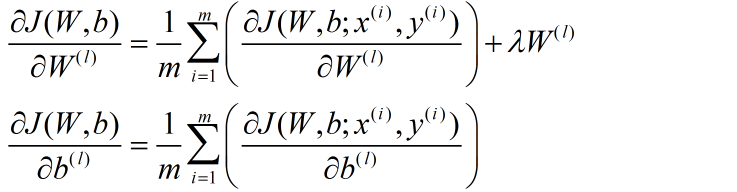
自编码算法与稀疏性
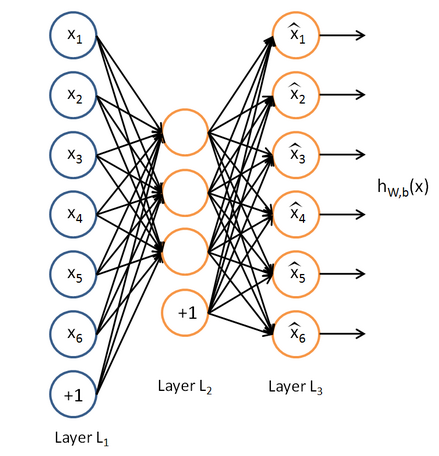
自编码器要求输出尽可能等于输入，并且它的隐藏层必须满足一定的稀疏性，即隐藏层不能携带太多信息。所以隐藏层对输入进行了压缩，并在输出层中解压缩。整个过程肯定会丢失信息，但训练能够使丢失的信息尽量少。
为了保证隐藏层的稀疏性，自动编码器的代价方程加入了一个稀疏性惩罚项：
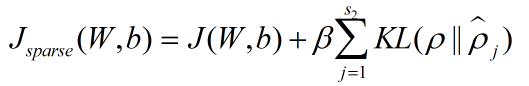
其中：
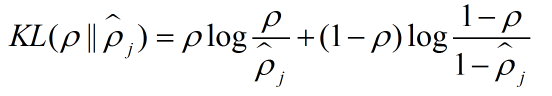
因为代价方程多了一项，所以梯度的表达式也有变化：
稀疏性惩罚项只需要第 1 层参数参与计算，令
所以
所以
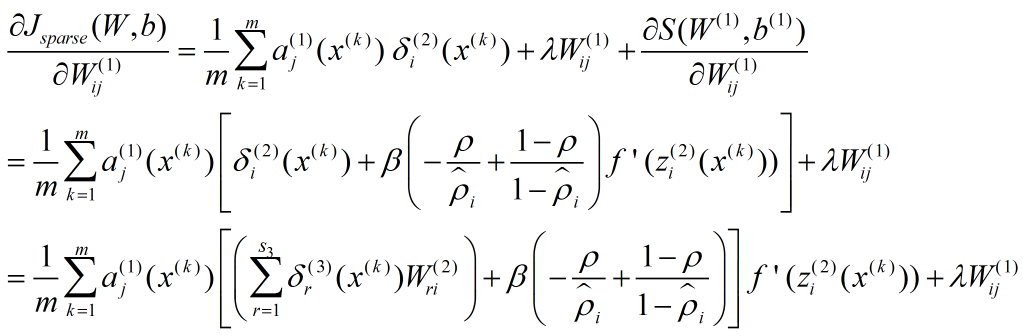
相当于
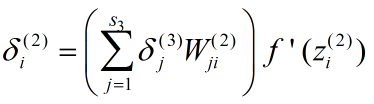
变成
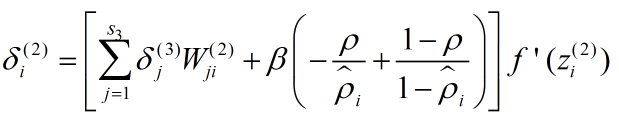
可视化自动编码器的训练结果
训练完（稀疏）自编码器，我们还想把这自编码器学到的函数可视化出来，好弄明白它到底学到了什么。
已知：
什么样的输入 x 可让 
得到最大程度的激励？
假设输入有范数约束：
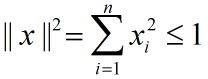
要使 最大，只需要使
最大即可，因为 f 是单调递增函数（此处忽略了截距项），令其为表达式（1）。
使（1）取得最大值的 x 一定满足：
因为超平面的最值一定在闭合区域的边界上取得。
把（1）改写成：
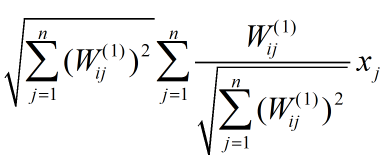
令
表达式（1）可重写为：
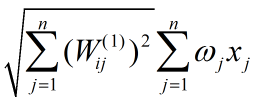
这是两个模为1的向量的内积乘以一个常数，当两个向量重合时它取到最值，即：
最值为：
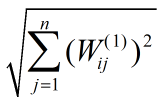
课后练习
在 MATLAB 命令行界面输入：
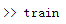
执行结果：
训练结果可视化：
