变分推断(Variational Inference)
变分
对于普通的函数f(x),我们可以认为f是一个关于x的一个实数算子,其作用是将实数x映射到实数f(x)。那么类比这种模式,假设存在函数算子F,它是关于f(x)的函数算子,可以将f(x)映射成实数F(f(x)) 。对于f(x)我们是通过改变x来求出f(x)的极值,而在变分中这个x会被替换成一个函数y(x),我们通过改变x来改变y(x),最后使得F(y(x))求得极值。
变分:指的是泛函的变分。打个比方,从A点到B点有无数条路径,每一条路径都是一个函数吧,这无数条路径,每一条函数(路径)的长度都是一个数,那你从这无数个路径当中选一个路径最短或者最长的,这就是求泛函的极值问题。有一种老的叫法,函数空间的自变量我们称为宗量(自变函数),当宗量变化了一点点而导致了泛函值变化了多少,这其实就是变分。变分,就是微分在函数空间的拓展,其精神内涵是一致的。求解泛函变分的方法主要有古典变分法、动态规划和最优控制。
变分推断
推了这么多公式,让我们先喘口气,来看看这些公式究竟在做什么?
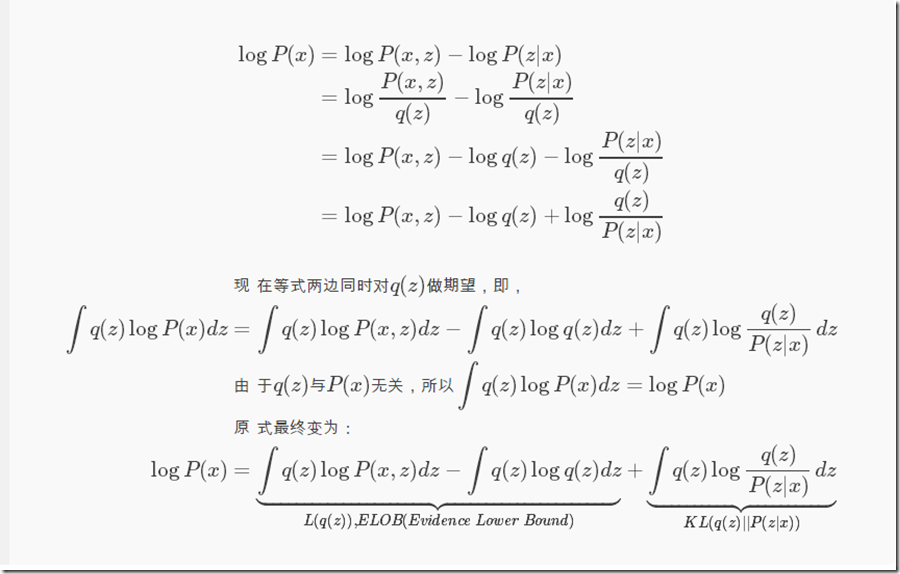
对于一类数据x(无论是音频还是图片),对它们进行编码后得到的特征数据往往服从某种分布q(z),z为隐变量,q(z)这个隐含分布我们无法得知,但是我们可以通过现有数据X来推断出q(z),即P(z|x)。KL散度是用来衡量两个分布之间的距离,当距离为0时,表示这两个分布完全一致。P(x)不变,那么想让KL(q(z)||P(z|x))越小,即让ELOB越大,反之亦然。因为KL≥0,所以logP(x)≥ELOB。这个结论还可以通过下面的公式同样得到:
这段公式推导的关键在于中间的不等式部分,即Jensen不等式:
变分贝叶斯(Variational Bayes)
变分贝叶斯学习算法通常也是变分贝叶斯期望最大(Variantional Bayesian Expectation Maximization)VBEM算法,是广义化的EM算法。
变分贝叶斯是一类用于贝叶斯估计和机器学习领域中近似计算复杂(intractable)积分的技术。它主要应用于复杂的统计模型中,这种模型一般包括三类变量:观测变量(observed variables, data),未知参数(parameters)和潜变量(latent variables)。在贝叶斯推断中,参数和潜变量统称为不可观测变量(unobserved variables)。变分贝叶斯方法主要是两个目的:
近似不可观测变量的后验概率,以便通过这些变量作出统计推断。近似求P(Z|D)
对一个特定的模型,给出观测变量的边缘似然函数(或称为证据,evidence)的下界。主要用于模型的选择,认为模型的边缘似然值越高,则模型对数据拟合程度越好,该模型产生Data的概率也越高。
对于第一个目的,蒙特卡洛模拟,特别是用Gibbs取样的MCMC方法,可以近似计算复杂的后验分布,能很好地应用到贝叶斯统计推断。此方法通过大量的样本估计真实的后验,因而近似结果带有一定的随机性。与此不同的是,变分贝叶斯方法提供一种局部最优,但具有确定解的近似后验方法。
从某种角度看,变分贝叶斯可以看做是EM算法的扩展,因为它也是采用极大后验估计(MAP),即用单个最有可能的参数值来代替完全贝叶斯估计。另外,变分贝叶斯也通过一组相互依然(mutually dependent)的等式进行不断的迭代来获得最优解。
问题描述
重新考虑一个问题:1)有一组观测数据D,并且已知模型的形式,求参数与潜变量(或不可观测变量)Z={Z1,...,Zn}的后验分布: P(Z|D)。
正如上文所描述的后验概率的形式通常是很复杂(Intractable)的,对于一种算法如果不能在多项式时间内求解,往往不是我们所考虑的。因而我们想能不能在误差允许的范围内,用更简单、容易理解(tractable)的数学形式Q(Z)来近似P(Z|D),即 P(Z|D)≈Q(Z)。
由此引出如下两个问题:
假设存在这样的Q(Z),那么如何度量Q(Z)与P(Z|D)之间的差异性 (dissimilarity).
如何得到简单的Q(Z)?
对于问题一,幸运的是,我们不需要重新定义一个度量指标。在信息论中,已经存在描述两个随机分布之间距离的度量,即相对熵,或者称为Kullback-Leibler散度。
对于问题二,显然我们可以自主决定Q(Z)的分布,只要它足够简单,且与P(Z|D)接近。然而不可能每次都手工给出一个与P(Z|D)接近且简单的Q(Z),其方法本身已经不具备可操作性。所以需要一种通用的形式帮助简化问题。那么数学形式复杂的原因是什么?在“模型的选择”部分,曾提到Occam’s razor,认为一个模型的参数个数越多,那么模型复杂的概率越大;此外,如果参数之间具有相互依赖关系(mutually dependent),那么通常很难对参数的边缘概率精确求解。
幸运的是,统计物理学界很早就关注了高维概率函数与它的简单形式,并发展了平均场理论。简单讲就是:系统中个体的局部相互作用可以产生宏观层面较为稳定的行为。于是我们可以作出后验条件独立(posterior independence)的假设。即,∀i,p(Z|D)=p(Zi|D)p(Z−i|D)
Kullback-Leibler散度
在统计学中,相对熵对应的是似然比的对数期望,相对熵 D(p||q)度量当真实分布为 P而假定分布为Q时的无效性。
为了极大化L(q),我们需要选择合适的函数q,使其便于计算。要注意到L(q)并非普通的函数,而是以函数q为自变量的函数,这就是泛函。泛函可以看成是函数概念的推广,而变分方法是处理泛函的数学领域,和处理函数的普通微积分相对。变分法最终寻求的是极值函数:它们使得泛函取得极大或极小值。
Gibbs Sampling这一类Monte Carlo算法,它们的做法就是通过抽取大量的样本估计真实的后验分布。而变分推断不同,与此不同的是,变分推断限制近似分布的类型,从而得到一种局部最优,但具有确定解的近似后验分布。
求解过程(极大化L(q))
根据以上假设,我们来最大化下界L(q),因为假设qi(Zi)分布之间都是独立的,所以我们依次轮流来优化,以qj(Zj)为例(为了简单起见,缩写为qj)。
这里我们定义一个新分布lnp~(X,Zj)为
我们发现它刚好是除去与qj分布相关的zj之后原似然的期望值,有
然后看式(5)的最后部分,就是qj(Zj)和p~(X,Zj)的KL散度的负值,这里我们固定qi≠j不变,那么最大化L(q)就变成了最小化这个KL散度,而KL 散度的最小值在qj(Zj)=lnp~(X,Zj)时取到。所以,最优解q∗j(Zj)为
另加的这个C是为了归一化整个分布,有![]() 然后依次更新其他Zj,最终相互迭代达到稳定。
然后依次更新其他Zj,最终相互迭代达到稳定。
变分下界
我们也可以直接衡量模型的下界。在实际应用中,变分下界可以直接判断算法是否收敛,也可以通过每次迭代都不会降低这一点来判断算法推导和实现的部分是否存在问题。
平均场理论(Mean Field Method)
数学上说,平均场的适用范围只能是完全图,或者说系统结构是well-mixed,在这种情况下,系统中的任何一个个体以等可能接触其他个体。反观物理,平均场与其说是一种方法,不如说是一种思想。其实统计物理的研究目的就是期望对宏观的热力学现象给予合理的微观理论。物理学家坚信,即便不满足完全图的假设,但既然这种“局部”到“整体”的作用得以实现,那么个体之间的局部作用相较于“全局”的作用是可以忽略不计的。
根据平均场理论,变分分布Q(Z)可以通过参数和潜在变量的划分(partition)因式分解,比如将Z划分为Z1…ZM
注意这里并非一个不可观测变量一个划分,而应该根据实际情况做决定。当然你也可以这么做,但是有时候,将几个潜变量放在一起会更容易处理。
通俗理解平均场
假设有一个很大很大的教室,里面坐着很多很多的学生,这些学生都在晨读,你是其中的一员。你听到的声音是所有学生发出的声音到拟这个位置的叠加,显然这个求和很复杂,因为你的听觉感受与声源到你的距离有关。为了简化这个求和,我们把所有学生在你这个位置产生的声音效果看作是噪音。如果这个教室真的足够大,大到我们可以忽略边界效应。现在,换一个场景,如果所有学生保持战斗队列(继续晨读),你现在是一位老师,在教室里巡视。然后无论你走到哪里,你的听觉感受都是一样的。这个噪音在任何位置都一样,无论往前走还是往右走一步都一样,这就是平移不变性。这个时候,噪音和一个均匀外场产生的效果一样,这个噪音就是平均场。
平均场方法的合理性
在量子多体问题中,用一个(单体)有效场来代替电子所受到的其他电子的库仑相互作用。这个有效场包含所有其他电受到的其他电子的库仑相互作用。这个有效场包含了所有其他电子对该电子的相互作用。利用有效场取代电子之间的库仑相互作用之后,每一个电子在一个有效场中运动,电子与电子之间的运动是独立的(除了需要考虑泡利不相容原理),原来的多体问题转化为单体问题。
于是,对于某个划分Zi,我们可以先保持其他划分Z−i不变,然后用以上关系式更新Zi。相同步骤应用于其他划分的更新,使得每个划分之间充分相互作用,最终达到稳定值。
具体更新边缘概率(VB-marginal)步骤如下:
平均场估计下边缘概率的无意义性 (VB-marginals)
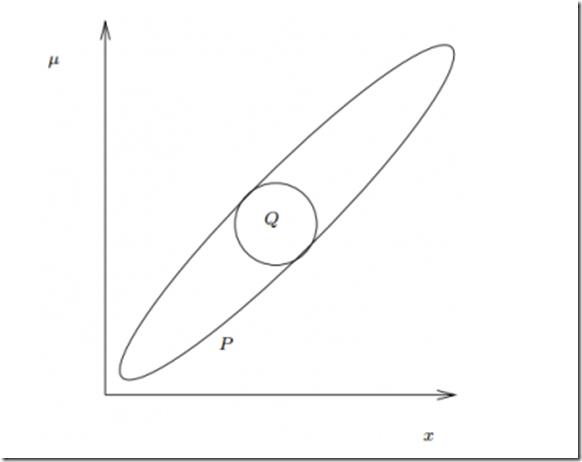
注意到Q(Z)估计的是联合概率密度,而对于每一个Qi(Zi),其与真实的边缘概率密度Pi(Zi)的差别可能是很大的。不应该用Qi(Zi)来估计真实的边缘密度,比如在一个贝叶斯网络中,你不应该用它来推测某个节点的状态。而这其实是很糟糕的,相比于其他能够使用节点状态信息来进行局部推测的算法,变分贝叶斯方法更不利于调试。
比如一个标准的高斯联合分布P(μ,x)和最优的平均场高斯估计Q(μ,x)。Q选择了在它自己作用域中的高斯分布,因而变得很窄。此时边缘密度Qx(x)变得非常小,完全与Px(x)不同。
泛函的概念
上文已经提到我们要找到一个更加简单的函数D(Z)来近似P(Z|D),同时问题转化为求解证据logP(Z)的下界L(Q),或者L(Q(Z))。应该注意到L(Q)并非普通的函数,而是以整个函数为自变量的函数,这便是泛函。我们先介绍一下什么是泛函,以及泛函取得极值的必要条件。
泛函
设对于(某一函数集合内的)任意一个函数y(x),有另一个数J[y]与之对应,则称J[y]为y(x)的泛函。泛函可以看成是函数概念的推广。 这里的函数集合,即泛函的定义域,通常要求y(x) 满足一定的边界条件,并且具有连续的二阶导数.这样的y(x)称为可取函数。
泛函不同于复合函数
例如g=g(f(x)); 对于后者,给定一个x值,仍然是有一个g值与之对应; 对于前者,则必须给出某一区间上的函数y(x),才能得到一个泛函值J[y]。(定义在同一区间上的)函数不同,泛函值当然不同, 为了强调泛函值J[y]与函数y(x)之间的依赖关系,常常又把函数y(x)称为变量函数。
参考文献:
http://blog.csdn.net/GZHermit/article/details/66472671








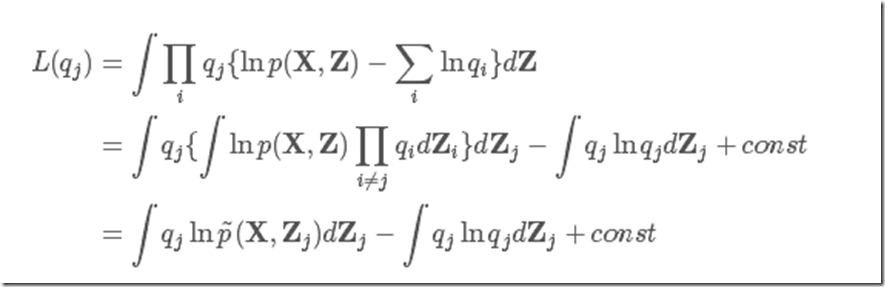
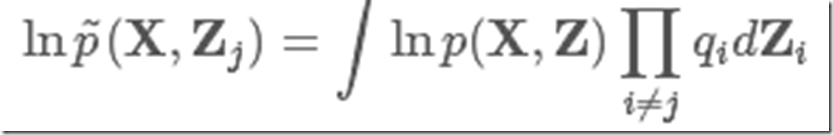
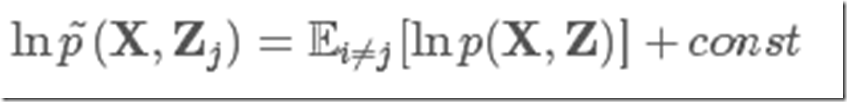
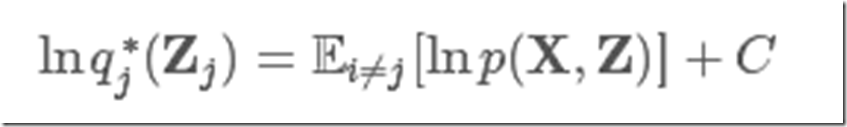
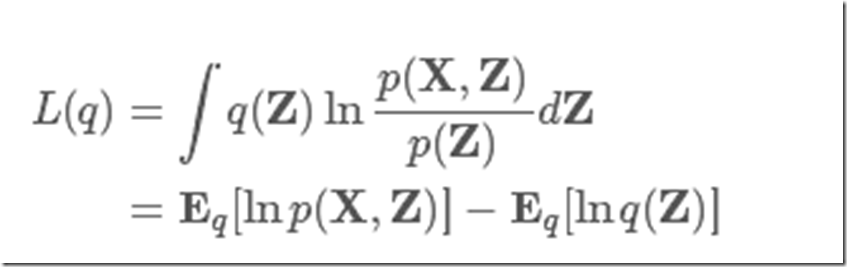
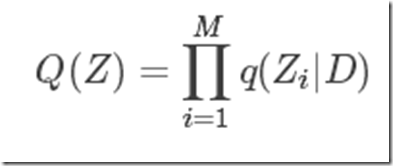





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
· 三行代码完成国际化适配,妙~啊~