Q-learning
强化学习基本介绍
强化学习是一种不同于监督学习和无监督学习的在线学习技术,基本模型图一所示。它把学习看作是一个“试探一评价”的过程,首先学习系统称为智能体感知环境状态,采取某一个动作作用于环境,环境接受该动作后状态发生变化,同时给出一个回报奖励或惩罚反馈给强化学习系统,强化学系统根据强化信号和环境的当前状态再选择下一个动作,选择的原则是使受到再励的概率增大。
智能体在和环境交互时,在每一时刻会发生如下事件序列
1)智能体感知t时刻的环境状态s(t)
2)针对当前的状态和即时回报r(t),智能体选择一执行动作a(t)。
3)当智能体所选择的动作作用于环境时,环境发生变化
环境状态转移至下一新的状态s(t+1)
给出即时回报r(t),又称为奖赏回报
4)即时回报r(t)反馈给智能体,t<-t+1,。
5)转向第2步,如果新的状态为结束状态,则停止循环。
其中即时回报r(t),由环境状态s(t)与智能体的输出a(t)决定。a∈A,A为一组动作集。
基本知识
1.评价函数
智能体的学习目标是最大化未来回报的累积值。评价函数,是对长期回报的一种量度,有三种返回表达式。
1)有限范围模型它是在有限的阶段内对回报的累积。为采样时刻,为智能体从时刻起到结束运行的总步数,可以不预先确定
2)折扣回报无限范围模型它是在无限的阶段内对回报的累积。
γ是折扣因子,通常0≤γ<1。通过调节,可以控制学习系统对它自己行动的短期和长期结果考虑的程度。在极端情况,当γ=0时系统是短视的,它只考虑行动的当前结果。当γ接近1时,未来的回报在采取最优行动时变得更为重要.
3)平均回报模型一采用第三种标准,累计未来回报的平均值,标准为
上面三种回报表达式,使用最多的是折扣回报指标。
马尔可夫决策过程(MDP)
大家应该还记得马尔科夫链(Markov Chain),了解机器学习的也都知道隐马尔可夫模型(Hidden Markov Model,HMM)。它们具有的一个共同性质就是马尔可夫性(无后效性),也就是指系统的下个状态只与当前状态信息有关,而与更早之前的状态无关。
马尔可夫决策过程(Markov Decision Process, MDP)也具有马尔可夫性,与上面不同的是MDP考虑了动作,即系统下个状态不仅和当前的状态有关,也和当前采取的动作有关。还是举下棋的例子,当我们在某个局面(状态s)走了一步(动作a),这时对手的选择(导致下个状态s’)我们是不能确定的,但是他的选择只和s和a有关,而不用考虑更早之前的状态和动作,即s’是根据s和a随机生成的。
我们用一个二维表格表示一下,各种马尔可夫子模型的关系就很清楚了:
一个马尔可夫决策过程由一个四元组构成M = (S, A, Psa, )
- S: 表示状态集(states),有s∈S,si表示第i步的状态。
- A:表示一组动作(actions),有a∈A,ai表示第i步的动作。
- sa: 表示状态转移概率。s 表示的是在当前s ∈ S状态下,经过a ∈ A作用后,会转移到的其他状态的概率分布情况。比如,在状态s下执行动作a,转移到s'的概率可以表示为p(s'|s,a)。
- R: S×A⟼ℝ ,R是回报函数(reward function)。有些回报函数状态S的函数,可以简化为R: S⟼ℝ。如果一组(s,a)转移到了下个状态s',那么回报函数可记为r(s'|s, a)。如果(s,a)对应的下个状态s'是唯一的,那么回报函数也可以记为r(s,a)。
MDP 的动态过程如下:某个智能体(agent)的初始状态为s0,然后从 A 中挑选一个动作a0执行,执行后,agent 按Psa概率随机转移到了下一个s1状态,s1∈ Ps0a0。然后再执行一个动作a1,就转移到了s2,接下来再执行a2…,我们可以用下面的图表示状态转移的过程。
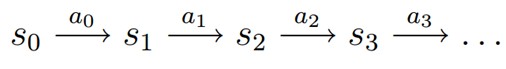
如果回报r是根据状态s和动作a得到的,则MDP还可以表示成下图:
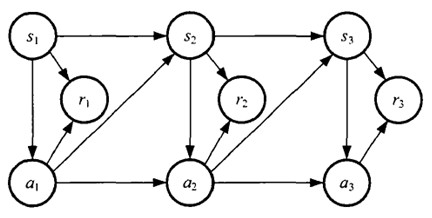
马尔科夫决策问题的目的是寻求一个最优策略,即使评价函数最大化的一系列动作。对于每一时刻的状态s(t),智能体均会通过最优策略π选取适当的动作。
而增强学习的目的就是求解马尔可夫决策过程(MDP)的最优策略。
那么如何求解最优策略呢?基本的解法有三种:
1.动态规划法(dynamic programming methods)
2.蒙特卡罗方法(Monte Carlo methods)
3.时间差分法(temporal difference)。
动态规划法是其中最基本的算法。
Q-learning基本介绍
Q一学习是强化学习的主要算法之一,是一种无模型的学习方法,它提供智能系统在马尔可夫环境中利用经历的动作序列选择最优动作的一种学习能力。Q-学习基于的一个关键假设是智能体和环境的交互可看作为一个Markov决策过程(MDP),即智能体当前所处的状态和所选择的动作,决定一个固定的状态转移概率分布、下一个状态、并得到一个即时回报。Q-学习的目标是寻找一个策略可以最大化将来获得的报酬。
Q-Learning是一项无模型的增强学习技术,它可以在MDP问题中寻找一个最优的动作选择策略。它通过一个动作-价值函数来进行学习,并且最终能够根据当前状态及最优策略给出期望的动作。它的一个优点就是它不需要知道某个环境的模型也可以对动作进行期望值比较,这就是为什么它被称作无模型的。
Q--learning中,每个Q(s,a)对应一个相应的Q值,在学习过程中根据Q值,选择动作。Q值的定义是如果执行当前相关的动作并且按照某一个策略执行下去,将得到的回报的总和。最优Q值可表示为Q+,其定义是执行相关的动作并按照最优策略执行下去,将得到的回报的总和,其定义如下:
其中:s表示状态集,A表示动作集,T(s,a,s’)表示在状态s下执行动作a,转换到状态s’的概率,r(s,a)表示在状态s下执行动作a将得到的回报,表示折扣因子,决定时间的远近对回报的影响程度。
智能体的每一次学习过程可以看作是从一个随机状态开始,采用一个策略来选择动作,如ε贪婪策略或Boltzamann分布策略。采用随机策略是为了保证智能体能够搜索所有可能的动作,对每个Q(s,a)进行更新。智能体在执行完所选的动作后,观察新的状态和回报,然后根据新状态的最大Q值和回报来更新上一个状态和动作的Q值。智能体将不断根据新的状态选择动作,直至到达一个终止状态。下面给出Q—learning算法的描述:

每次更新我们都用到了 Q 现实和 Q 估计, 而且 Q-learning 的迷人之处就是 在 Q(s1, a2) 现实 中, 也包含了一个 Q(s2) 的最大估计值, 将对下一步的衰减的最大估计和当前所得到的奖励当成这一步的现实, 很奇妙吧. 最后我们来说说这套算法中一些参数的意义. ε greedy 是用在决策上的一种策略, 比如 ε= 0.9 时, 就说明有90% 的情况我会按照 Q 表的最优值选择行为, 10% 的时间使用随机选行为. α是学习率, 来决定这次的误差有多少是要被学习的, α是一个小于1 的数. γ是对未来 reward 的衰减值. 我们可以这样想象.
Q-learning 是一个 off-policy 的算法, 因为里面的 max action 让 Q table 的更新可以不基于正在经历的经验(可以是现在学习着很久以前的经验,甚至是学习他人的经验).
On-policy 与 off-policy 本质区别在于:更新Q值时所使用的方法是沿用既定的策略(on-policy)还是使用新策略(off-policy)
以后要讲的Sarsa算法是on-policy的。也就是说,Sarsa算法在更新Q表的时候所遵循的策略与当前策略一致。
实例:(Flappy Bird Q-learning)
问题分析
让小鸟学习怎么飞是一个强化学习(reinforcement learning)的过程,强化学习中有状态(state)、动作(action)、奖赏(reward)这三个要素。智能体(Agent,在这里就是指我们聪明的小鸟)需要根据当前状态来采取动作,获得相应的奖赏之后,再去改进这些动作,使得下次再到相同状态时,智能体能做出更优的动作。
状态的选择 在这个问题中,状态的提取方式可以有很多种:比如说取整个游戏画面做图像处理啊,或是根据小鸟的高度和管子的距离啊。在这里选用的是跟SarvagyaVaish项目相同的状态提取方式,即取小鸟到下一根下侧管子的水平距离和垂直距离差作为小鸟的状态:

(图片来自Flappy Bird RL by SarvagyaVaish)
记这个状态为,
为水平距离,
为垂直距离。
动作的选择 小鸟只有两种动作可选:1.向上飞一下,2.什么都不做。
奖赏的选择 这里采用的方式是:小鸟活着时,每一帧给予1的奖赏;若死亡,则给予-1000的奖赏;若成功经过一个水管,则给予50的奖赏。
关于Q
提到Q-learning,我们需要先了解Q的含义。
Q为动作效用函数(action-utility function),用于评价在特定状态下采取某个动作的优劣,可以将之理解为智能体(Agent,我们聪明的小鸟)的大脑。我们可以把Q当做是一张表。表中的每一行是一个状态,每一列(这个问题中共有两列)表示一个动作(飞与不飞)。
例如:
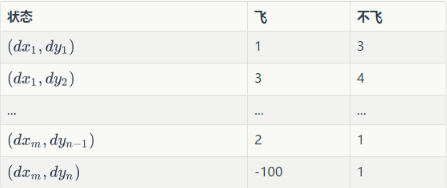
这张表一共 行,表示
个状态,每个状态所对应的动作都有一个效用值。训练之后的小鸟在某个位置处飞与不飞的决策就是通过这张表确定的。小鸟会先去根据当前所在位置查找到对应的行,然后再比较两列的值(飞与不飞)的大小,选择值较大的动作作为当前帧的动作。
训练
那么这个Q是怎么训练得来的呢,贴一段伪代码。
Initialize Q arbitrarily //随机初始化Q值
Repeat (for each episode): //每一次游戏,从小鸟出生到死亡是一个episode
Initialize S //小鸟刚开始飞,S为初始位置的状态
Repeat (for each step of episode):
根据当前Q和位置S,使用一种策略,得到动作A //这个策略可以是ε-greedy等
做了动作A,小鸟到达新的位置S',并获得奖励R //奖励可以是1,50或者-1000
Q(S,A) ← (1-α)*Q(S,A) + α*[R + γ*maxQ(S',a)] //在Q中更新S
S ← S'
until S is terminal //即到小鸟死亡为止
其中有两个值得注意的地方
1.“根据当前Q和位置S,使用一种策略,得到动作A,这个策略可以是ε-greedy等。”
这里便是题主所疑惑的问题,如何在探索与经验之间平衡?假如我们的小鸟在训练过程中,每次都采取当前状态效用值最大的动作,那会不会有更好的选择一直没有被探索到?小鸟一直会被桎梏在以往的经验之中。而假若小鸟在这里每次随机选取一个动作,会不会因为探索了太多无用的状态而导致收敛缓慢?
于是就有人提出了ε-greedy方法,即每个状态有ε的概率进行探索(即随机选取飞或不飞),而剩下的1-ε的概率则进行开发(选取当前状态下效用值较大的那个动作)。ε一般取值较小,0.01即可。当然除了ε-greedy方法还有一些效果更好的方法,不过可能复杂很多。
以此也可以看出,Q-learning并非每次迭代都沿当前Q值最高的路径前进。
2.
这个就是Q-learning的训练公式了。其中α为学习速率(learning rate),γ为折扣因子(discount factor)。根据公式可以看出,学习速率α越大,保留之前训练的效果就越少。折扣因子γ越大,所起到的作用就越大。但
指什么呢?
小鸟在对状态进行更新时,会考虑到眼前利益(R),和记忆中的利益()。
指的便是记忆中的利益。它是指小鸟记忆里下一个状态
的动作中效用值的最大值。如果小鸟之前在下一个状态
的某个动作上吃过甜头(选择了某个动作之后获得了50的奖赏),那么它就更希望提早地得知这个消息,以便下回在状态
可以通过选择正确的动作继续进入这个吃甜头的状态
。
可以看出,γ越大,小鸟就会越重视以往经验,越小,小鸟只重视眼前利益(R)。
根据上面的伪代码,就可以写出Q-learning的代码了。
成果

训练后的小鸟一直挂在那里可以飞到几千分~
参考文献:
https://www.cnblogs.com/jinxulin/p/3517377.html
http://blog.csdn.net/duanyajun987/article/details/78614902?locationNum=2&fps=1
https://zhuanlan.zhihu.com/p/24808797
https://www.zhihu.com/question/26408259/answer/123230350



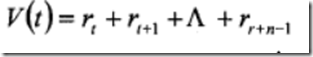
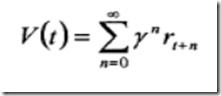
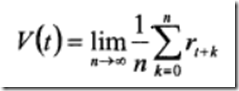

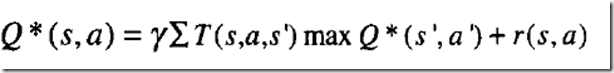



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
· 三行代码完成国际化适配,妙~啊~